elsur.jpn.org >

« 2017年3月 | メイン | 2017年9月 »

2017年8月28日 (月)

引き続き、6月頃にとったメモ。これは外出先のコーヒーショップでメモした覚えがある... なにかの時間待ちだったと思うのだが、全然思い出せない。

Smith, B., Linden, G. (2017) Two Decades of Recommendation Systems at Amazon.com. IEEE Internet Computing, 21(3), 12-18.

　たまたまみつけた面白い記事。
　いきさつとしては... IEEE Internet Computing誌20周年を記念して、過去の重要論文を選び表彰することにした。栄えある第一回受賞者は、2003年に掲載された"Amazon.com Recommendations", 著者はamazon.comのなかの人であるLinden, Smith, Yorkの三名。おめでとうございます。
　というわけで、著者のみなさんにその後を振り返っていただくことにしました... という主旨。受賞論文の第一著者であるLindenさんは、この論文ではMicrosoft所属になっており、時の流れを感じさせます。
　せっかくなので受賞講演風にメモ。

　どうもありがとう... ありがとう... (拍手が鳴りやむのを待つ)
　これまでの20年間に渡り、amazon.comは個々の顧客のためのお店を作って参りました。(ここで気の利いたジョークを一発かまして笑いを取る)
　amazon.comの推薦システムは、あなたの現在の文脈と過去の行動に基づき、あなたに喜んで頂けそうな少数のアイテムをピックアップします。私たちがアイテム・ベース協調フィルタリングをローンチしたのが1998年。IEEE Internet Computing誌でアルゴリズムを紹介したのが2003年。このアルゴリズムはいまやWebにあまねく広がっております。

　90年代中期の協調フィルタリングは基本的にユーザ・ベースでした。つまり、まずあなたと関心が類似している人を探し、次にその人たちが買っていてあなたが買っていないアイテムを探すというものでした。
　それに対して私たちのアルゴリズムはこうでした。あらかじめ、カタログ上の個々のアイテムについてそれと関連したアイテムを探しておきます。ここで「関連している」というのは、とりあえずは、いっぽうを買った人は他方も買いやすい、ということだとお考えください。この表を参照して、個々の顧客へのお勧めを素早く生成します。このアルゴリズムなら、ほとんどの計算をオフラインで済ますことができます。こうして得られるお勧めは高品質かつ有用、サンプリングなどの手法を使わなくても大規模データに対応できます。

　2003年の出版の時点で、アイテム・ベース協調フィルタリングはamazon.comで広く採用されていました。ホームページ、検索結果、ショッピングカート、注文終了後画面、eメール、商品明細ページ、などなど。amazon.com以外にも広がりました。2010年にはYouTubeが採用したと伝えられております。オープン・ソースやサード・パーティ・ベンダーの推薦システムにも広く採用されました... [ちょっと中略]
　ではここからは、私たちが行ったアルゴリズム改善についてお話ししましょう。

　推薦システムは、突き詰めていえば統計学の応用です。人間の行動はノイジーであり、ランダム性のなかから有用なパターンを見つけるというのがここでの課題です。
　アイテム$X$と$Y$の両方を買う顧客の人数$N_{XY}$を推定するという問題について考えてみましょう。ひとつの自然なやり方は、$X$の購入者が$Y$を買う確率は一般の母集団のそれに等しい、すなわち
　$P(Y) = $(Yの購入者数)/(全購入者数)
と考えて、
　$E_{XY}=$ (Xの購入者) x $P(Y)$
を推定値とすることです。
　しかし興味深いことに、たいていの$X$と$Y$において、$X$の購入者が$Y$を買う程度は、一般の母集団のそれよりも高くなります。ヘビー・バイヤーがいるからです。いいかえると、購買を無作為に抽出すると、顧客の抽出確率は一様にならないわけです。
　そこで私たちはこう考えました。商品$X$を購入した顧客$c$について(これを$c \in X$と書くことにします)、その人が$Y$を買う確率は $1-(1-P_Y)^{|c|}$ だと考えます。ここで$P_Y$=(Y購入)/(全購入), $|c|$は$c$が$X$以外のなにかを買った回数です。たとえば$c$さんが20回買い物したら、$Y$を買う独立なチャンスが20回あったと考えるわけです。ここから
　$E_{XY} = \sum_{c \in X} \left( 1-(1-P_Y)^{|c|} \right)$
ここから次式が得られます：
　$E_{XY} = \sum_{k=1}^{\infty} \left( P^k_Y \sum_{c \in X} (-1)^{k+1} \binom{|c|}{k} \right)$
ここで$P_Y$は小さいですから、有界の$k$で近似できます。$P_Y$と$\sum_{c \in X} (-1)^{k+1} \binom{|c|}{k}$はあらかじめアイテムごとに算出しておくことができます。これを組み合わせて$E_{XY}$を素早く算出できるわけです。

　さて、この$E_{XY}$を実際の併買者数$N_{XY}$と比べれば、2商品間の類似性スコア$S(X, Y)$をつくることができます。たとえば非ランダム共起数$N_{XY}-E_{XY}$を使うという手もありますが、$Y$がハリーポッターだったりすると高くなるという難点があります。$(N_{XY}-E_{XY})/E_{XY}$とする手もありますが、今度は販売量が低いアイテムがどんどんお勧めされることになりますね。うまくバランスを取ってやる必要があります。たとえばカイ二乗スコア$(N_{XY}-E_{XY})/\sqrt{E_{XY}}$を使うとか。
　他にもいろいろ方法はあります。私たちの経験に基づいていえば、あらゆる場面において最良なスコアは存在しません。場面ごとに、機械学習や統制実験によってパラメータの最適化を図ります。

　[関連性の指標が良くてデータが十分なら、関連アイテムの意味づけはデータから創発する、という話。デジタルカメラのメモリカードの互換性が関連アイテムで表現されるとか。さいでございますか。中略]

　推薦の品質を向上するためには...

　未来の推薦システムはどのようなものになるでしょうか？
　私たちはこう想像しています。それは買い物をまるで会話のように簡単なものとしてくれる知的なインタラクティブ・サービスになる。あたかも、あなたのことをよく知っている友達とおしゃべりしているかのような。
　すべてのインタラクションがあなたの好みを反映する。もしあきらかにあなた向きでないものがおすすめされたら、まったくもう、あなたはまだ私のことがわかってないのね？ という気持ちになる(場内笑い)。ひとことでいえば、どこでも人工知能、ですね。
　こういう未来を実現するためには発想の転換が必要です。推薦システムの特徴やエンジンを改善するという問題ではありません。あなたを理解し、他者を理解し、いまなにが利用可能かを理解することが、すべての相互作用における必須の部分となります。

　およそ20年前にamazon.comがローンチした推薦システムは、いまではWebのいたるところで用いられています。アイテム・ベース協調フィルタリングはいまでももっとも一般的な推薦アルゴリズムのひとつです。
　この領域はいまだ広く開かれており、多くのチャンスが残されています。推薦は発見であり、驚きと喜びを提供します。推薦、それはインタラクションそのものです。(キメ顔)
　御清聴ありがとうございました。(拍手)

　...あーあ。推薦するアイテムの多様性をどうやってチューニングしているのかに関心があったけど、やっぱし、あんまし詳しいことは説明してくれないんだなあ。そりゃまあ、企業秘密だよなあ...

論文：データ解析(2015-) - 読了：Smith & Linden (2017) amazon.com推薦システムの20年

2017年8月27日 (日)

Soper, B., Milford, G.E., & Rosenthal, G.T. (1995) Belief when evidence does not support theory. Psychology and Marketing, 12(5), 415–422
　マズローの欲求階層説の受容を題材とした警世のエッセイ、という感じの文章。

　いわく、
　マーケティング研究者は動機づけの心理学的研究に関心を向けてきた。動機づけについての心理学的諸概念(無意識の動機づけ、強化理論、帰属理論、効力感の理論など)は、良かれ悪しかれ、マーケティング分野での共有知識となっている。
　マーケティング分野でいまだにもっとも広く受け入れられている動機づけ理論はマズローの欲求階層説である。その直観的な妥当性がマーケターの琴線に触れるのであろう。
　それはわかるんだけど、科学の手続きとしてはどのくらい妥当性があるんだろうか？

　マーケティングの教科書には、マズロー理論があたかも証明済みの原理であるかのように登場することが多い。引用はMaslow(1943, Psych.Bull.)からMaslow(1954, "Motivation and Personality")に及ぶ。でもマズローの定式化があくまでtentativeなものであることにはあまり注意が払われていない。

　マズロー理論の実証研究についてみてみよう。その多くは組織研究の文脈でなされている。

　このように、マズローのアイデアには実証性が欠けている。
　しかるに、マーケティングの教科書の書き手は、実証性のなさをよく知っていながら、なおも欲求階層説を使ってマーケティング現象を説明することが多い。たとえば Ingram & LaForge (1989, "Sales Management")を見よ。いったいどうやったらそんな真似ができるのか。
　人は自分の立場を支持する証拠にもっとも強く影響される。自分の信念のもとになったデータが実は誤っていたとあとで教わっても、人は信念を変えない。科学者も結局は人だということを忘れてはならない。
　マーケティング研究はみずからを科学だと再三定義づけてきた。だったら科学的方法の原点に戻るべきだ。ここで問われているのは、マーケティングは科学かアートかということではない。マーケティングは科学なのか超科学なのかということだ。

　... ははは。面白いなあ。
　これ、理論というものをまじめに受け取るか、ストーリーを整理する道具程度のものと捉えて場当たり的に使い捨てるか、という温度差の問題なのかもしれないですね。

論文：マーケティング - 読了：Soper, Milford, Rosenthal (1995) マーケティング研究者って実証性がないと知っているにも関わらずよくマズローを引き合いに出すじゃん？あれってどうなの？

Gambrel, P.A., Cianci, R. (2003) Maslow's Hierarchy of Needs: Does it apply in a collectivist culture. The Journal of Applied Management and Entrepreneurship, 8(2), 143-161
　タイトルの通り、マズローの欲求階層説を集団主義的文化に適用できるか、という話。ちょっと思うところあって手に取った。正直、世に溢れるマズロー的与太話にはあまり付き合いたくないんだけど(すいません)、ほんとに世に溢れているんだから仕方がない、と思って。
　掲載誌についても著者についてもよくわからない(掲載誌は国内所蔵館なし、もしかすると紀要のようなものかもしれない。著者らは博士課程在籍中)。

　いわく。
　動機づけの理論は内容理論とプロセス理論に大別される。前者は行動をひきおこす要因に注目し、後者は行動が引き起こされるありかたに注目する。前者の代表例が、マズローの欲求階層説、ハーツバーグの二要因理論、マクレランドの三要因理論である。これらの研究はアメリカ生まれ、被験者もアメリカ人である。
　欲求階層説の多文化研究としてすでにHofstede(1983, J.Int.BusinessStud.)がある。Hofstedeの個人主義-集団主義の次元は動機づけの理論と直接に関連している。
　本研究ではマズローの欲求階層説が集団主義文化に適用できるかどうか調べます。

　... 途中で気が付いたのだが、これ、HofstedeとかSchwartzとかの論文を読んでまとめましたというものであった。タイトルにマズローの名を挙げつつもマズローを一本も引用しておらず、すべて孫引き。あっちゃー...
　というわけで、読んでないけど読了にしてしまおう。えーと、欲求階層説は中国にはあてはまらないんじゃないでしょうか、というようなお話である模様。

論文：心理 - 読了：Gambrel & Cianci (2003) マズローの欲求階層説は中国人にあてはまるのかどうか、文化差の先行研究を集めて読んで考えてみました

Koltlo-Rivera, M.E. (2006) Rediscovering the later version of Maslow's Hierarchy of Needs: Self-Transcendence and Opportunities for Theory, Research, and Unification. Review of General Psychology, 10(4), 302-307.
　調べ物のついでにざっと読んだ奴。掲載誌については全く知らないのだが、いちおうAPAの出版物でもあるし、そんなに変なものではないはずだ、と思って。(ciniiによれば所蔵館3館...)
　かの有名なマズローの欲求階層説は世間でなにかと誤解されておるので、マズローの晩年の著作に基づいて無知迷妄を正します、という論文である。なお、マズロー理論の実証性とかその批判的評価とか他理論との比較とか改訂とか、そういうのはこの論文の目的じゃないのでよろしくね、とのこと。

　時系列で辿ると、マズロー先生の1943年, 1954年の著作では、よく知られているように欲求階層は５階層だった(生理学的, 安全, 所属と愛, 自尊, 自己実現)。50年代末からマズローはpeak experiencesに関心を持つようになり(美的経験とか神秘的経験とか)、そこに関わる認知的活動を"Being-cognition"と呼んだ。ただし、これと自己実現との関係についてはよくわからんと述べていた。で、いろいろ考えた末 [ここ、逸話的な話が続くので中略]、マズローは階層の最上位に自己超越 self-transcendenceというのを付け加えるようになった。
　なお、自己実現と自己超越は異なるもので、どっちかだけを経験することがありうる。また、自己超越を経験するということと、人生において自己超越の欲求が優越的になるということとはまた別の問題。

　これまでのマズロー理解において自己超越という概念が無視されてきたのはなぜか。マズローがメジャーな著作できちんと説明する前に死んじゃったから、自己超越という概念が当時の心理学にとって受け入れがたいものだったから、そもそもマズローの動機づけ理論自体に問題があったから(それは厳密な意味での階層モデルではない)... といった理由が考えられる由。

　では、自己超越が追加された欲求階層説にはどういういいことがあるのか。

  1. 人生の目的という概念についての研究に貢献する。人生の意味とか目的というのは我々の世界観の一部を構成しているわけだけど、マズローの欲求階層はそれらの概念を組織化する枠組みを提供してくれる。自己超越という階層が追加されたことで枠組みがよりリッチになった。
  2. 利他的行動と社会的進歩とか知恵とかについての動機づけ上の基盤を提供する。社会学者Starkいわく、一神教は社会的進歩や科学の進歩の駆動力となった。これは自己超越に重心を置く動機づけ的立場と関係があるかも... さらにStanbergいうところの知能のバランス理論は自己超越という概念を含んでいて.. [申し訳ないけど関心なくなってきたので中略]
  3. 自爆テロみたいな宗教的暴力を理解するために自己超越という概念が有用。
  4. マズローの階層に自己超越という段階を含めることで、宗教・スピリチュアリティとパーソナリティ心理学・社会心理学との橋渡しができる。
  5. 自己超越は文化を構成する共通要素のひとつだ。伝統的ヒンズー文化とかを見よ。また、個人主義-集団主義という次元は自己実現と自己超越を動機づけ理論に含めることで概念化しやすくなる。

　云々。

　うーん...
　あらゆる理論的枠組みが直接に実証可能であるべきだとは思わない。だけど、２つの理論的枠組みを比べたとき、「こっちのほうが枠組みがリッチだから、きっと現象理解もリッチになるにちがいない」と主張するのは、果たしてアリなのだろうか？ 仮にそうならば、理論は際限なくリッチになっていきませんか？ どうもよくわからない。
　まあいいや、次にいこう、次に！

論文：心理 - 読了：Koltlo-Rivera(2006) マズローの欲求階層説の６個目の階層、それは自己超越だ

2017年8月26日 (土)

現実逃避の一環として、論文メモを整理。6月頃に読んだ奴。

松井剛 (2001) マズローの欲求階層理論とマーケティング・コンセプト. 一橋論叢, 126(5), 495-510.
　たまたまマズローについて資料を探していてみつけた紀要論文。

　著者の先生曰く。
　欲求階層理論への批判は２つに分けられる。

　著者による、マーケティング分野でのマズロー受容に対する批判。

　なぜマーケティング分野でマズローはこんなに受けるのか。
　まず、欲求に階層があるという考え方は常識に合致する(Kilbourne, 1987というのがreferされている)。さらに、欲求階層説はマーケティング・コンセプトと親和性が高い。通説によれば、50-60年代アメリカにおいてマーケティング志向の時代が到来しマーケティング・コンセプトが生まれた。マーケティング・コンセプトは、顧客志向、利益志向、統合的努力の３点から説明される。マーケティング・コンセプトは「ターゲット市場の欲求を明らかにして効率的・効果的に対応する点に、組織目標を達成する鍵があると考える『ビジネス哲学』なのである」。この変化を説明するのに、「低次欲求の充足が満たされると高次欲求が生まれる」「自己実現は誰にとっても望ましい」という理論は都合がよかったのではないか。
　云々。

　ディスプレイ上でざっと目を通しただけなので、読み落としがあるかもしれないけど、とても面白かったです。
　最後のくだりが著者の先生の力点だと思うけど、もう少し詳しい議論を読みたいものだ。欲求階層説には確かに「消費主義の守護神」的な側面があり、それがマーケティングとの親和性を生んでいるのかもしれないけど、そもそも欲求階層説は消費主義の奥にある、なにか現代人のエートスのようなものと深い親和性を持っていて、その結果としてマーケティングを含めた多様な領域で愛されちゃうのかもしれない、とも思う。だって、本屋さんで立ち読みしていると、有閑マダム向けの趣味の棚の雑誌には「素敵なインテリアで私らしい私を実現」とかって書いてあるし、ビジネス棚の本には「仕事での成功こそ自己実現」って書いてあるじゃないですか。この共通性はなんなのだろうと思うのである。

　ところで、マーケティングの教科書に書いてある「生産志向時代→販売志向時代→マーケティング志向時代」という歴史的発展は、史実には合わないそうだ。へぇー。Fullerton (1988, J.Mktg)というのを読むといいらしい。

論文：マーケティング - 読了：松井(2001) マーケティング関係者はなぜマズローが好きなのか

Reise, S.P. (2012) The Rediscovery of Bifactor Measurement Models. Multivariate Behavioral Research, 47(5), 667-696.

　SEMでいうbifactor model(「双因子モデル」？)についての解説。bifactorモデルには独特の話題があるので、前から気になっていたんだけど、勉強する機会がなかった。このたびちょっときっかけがあって大急ぎでめくった。

　いわく。
　bifactorモデルとは、ひとつの一般因子があって全項目がそれを反映し、それとは直交するいくつかのグループ因子(特殊因子)があってそれぞれが項目のクラスタに対応する、というモデル。前者は概念的に広いターゲット構成概念を表し、後者はより狭い下位領域の構成概念を反映する。[←ことばで表現するとわかりにくいっすね]
　bifactorモデルの歴史は1930年代に遡るが、サーストン流の因子間相関モデルの栄光の陰に忘れ去られ、さびれた港町で無為な日々を送っていた[←意訳]。それが最近急に注目されているのは、(1)パーソナリティ測定の分野で良く使われるようになり、(2)啓蒙論文が出版され、(3)方法論研究が増え、そして(4)ソフトが出てきたから。

探索的bifactorモデル
　30年代にHolzingerらが提案したのがこれ。50年代にSchmid-Leiman直交化(SL)という上手い推定方法が出てきた。でもあんまり使われてない。理由: (1)SLが一般的なソフトに載ってない。(2)研究者が不勉強。

　結局のところ、因子間相関モデル、二次因子モデル、SLは等価である。ということを、実データ(15項目, 5因子を想定)でお示ししましょう。

　まず因子間相関モデルから。モデルで再現する相関行列を$\hat{R}$として、
　$\hat{R} = \Lambda \phi \Lambda^T + \Theta$
と書ける。ただし$\Lambda$は$15 \times 5$の負荷行列、$\phi$は$5 \times 5$の因子間相関行列、$\Theta$は$15 \times 15$の直交行列で独自性を表す。心理測定の研究者が大好きなモデルである。個人差は因子得点のプロファイルとして表現される。因子は比較的に狭い構成概念を表している。全項目を通じた共通分散があるとして、それは$\phi$行列のなかに隠れている。

　同じデータに二次因子モデルを当てはめることもできる。$\phi$行列を単一の二次因子への負荷行列に変換するわけである。個人差は一般的傾向性(たとえば「一般的不安」とかね)と、より狭い下位傾向性によって表現される。ここでのポイントは、二次因子と項目の間に直接的な関連はない、という点だ。二次因子モデルは共通因子モデルの再表現に過ぎない。つまり、上のモデルの$\phi$について
　$\phi = \Gamma \Phi \Gamma^T + \Psi$
とモデル化しただけである。

　さて。次の変換行列$T$を考えます。
　$T=[\Gamma | \Psi^{1/2}]$
サイズは$5 \times 6$。1列目は、二次因子モデルにおける二次因子への負荷を表す。2列目以降は対角行列で、各一次因子の独自分散の平方根を持つ[えーっと、各行は2つの要素を持ち二乗和が1になるわけね]。これをつかって負荷行列を変換し
　$\hat{R} = (\Lambda T)(\Lambda T)^T + \Theta$
これがSL直交化である。[←なるほどねえ。こりゃ計算が楽だわね]
　SLでは、共通因子は一般的な次元を表し、グループ因子はそれと直交する下位領域を表す。切り離して解釈できるというのが美点。
　
　以上を整理しよう。因子間相関モデルの負荷行列が完全な独立クラスタ構造を持っているとき(=ある項目がある一次因子にのみ負荷を持つとき)、

　SLの怖いところ。

というわけで、SLに代わる現代的な推定方法が開発されている。Reise et al.(2011)のtarget bifactor回転と、Jennrich & Bentler (2011)のanalytic bifactor 回転がある。後者はRのpsychパッケージにも入っている。[実データの分析例が載っているけど、パス。なおMplusだとBI-GEOMIN回転とBI-CF-QUARTIMAX回転が使えて、どちらも斜交か直交かを選べる]

確認的bifactorモデル
　各項目は一般因子とどれかひとつのグループ因子だけに負荷を持つ、というモデル。比例性の問題はなくなるが、交差負荷を無視したせいで起きるバイアスが怖いので、ちゃんと探索的分析をやってから組むのが大事。
　
　推定方法。SEMアプローチとIRTアプローチを紹介しよう。2値データについて考える。[以下、誤植らしき箇所を勝手に直したり書き換えたりしている]

　SEMアプローチの場合。$i$番目の変数の背後に正規潜在反応変数$x_i^*$と閾値$\tau_i$を仮定する。グループ因子が$p$個だとして
　$x_i^* = \sum_{j=0}^p \lambda_{i,j} \theta_{j} + \eta_i$
　で、WLS推定とかを使ってテトラコリック相関行列を分析する。これを限定情報因子分析と呼ぶ(平均と共分散しか使わないから)。

　IRTアプローチの場合。モデルはこんな感じになる。
　$\displaystyle E(x_i|\theta) = \frac{\exp(z_i)}{1+\exp(z_i)}$
　$z_i = \sum_{j=0}^p \alpha_{i,j} \theta_j + \gamma_i$
$\alpha$が識別性、$\gamma$が困難度を表す。で、周辺最尤推定(marginal ML)を使って項目反応行列全体を分析する。これを完全情報因子分析と呼ぶ。
　
　よく知られているように、2パラメータ正規IRTと間隔尺度因子分析は等価である。$\alpha, \gamma$と$\lambda, \tau$のあいだには次のような関係があって...[略]
　ただし、以下の点に注意すべきである。

　[ここでモデル比較のデモ。bifactorモデル, 因子間相関モデル, 二次因子モデル, 一次元モデルを比べる。略]
　[一般因子のパラメータ不変性、つまり、使う項目を多少削ってもパラメータが大きく変わらないかどうかを調べるデモ。略]

bifactorモデルの使い道
では、bifactorモデルの重要な使い道を4つ、実例とともに紹介しましょう。

要約と限界

云々。

　ちょっと思ったことをメモ。
　調査データ分析の文脈では反応スタイルなどに起因する共通手法分散(CMV)が深刻な問題になる。この論文が主に対象としているのは、一般的心理特性と下位領域の心理特性を反映しているような心理尺度で、だからこそ、因子を直交させるのが推奨されているし、交差負荷もなしにするのが基本なのだと思う。でも私はどっちかというと、複雑なデータ生成構造を持つ調査データがあって、これからその構造について調べたいんだけど、まずはうまくCMVだけ取り除きたい、という場面を思い浮かべながら読んでいた。だから、一般因子とグループ因子の直交性仮定はいいけれど、グループ因子間の直交性仮定は強すぎて困るな、と思う。
　確認してないんだけど、CMVの第一人者(?)であるPodsakoffさんは以前「CMV因子を入れたCFA」案を紹介していたらしい。でもAntonakisらのレビューでは否定的に扱われていたと思う(モデルが誤指定だったらひどい目に合うから、というような理由だった)。リッカート尺度の項目群の場合、Allenby兄貴のようにHBモデルを組むというのがひとつの方向だと思うのだが、いかんせんめんどくさい。
　で、この論文を読んでいて思うに、カテゴリカルEFAでbifactor回転してモデルの誤指定をチェックした上で$\omega_H$を推定し、CMV因子をいれた好き勝手なSEM, ただしCMVへの負荷はさっきの$\omega_H$を再現できる値に全項目等値で固定する... というのはだめかしらん？ いつか暇ができたら調べてみたい。(まあ無理だけどな)

論文：データ解析(2015-) - 読了：Reise (2012) 忘却の淵から甦れ、bifactorモデルよ

2017年8月25日 (金)

Alvarez, I., Niemi, J., Simpson, M. (2014) Bayesian Inference for a Covariance Matrix. Proceedings of 26th Annual Conference on Applied Statistics in Agriculture, 71-82.
　ベイズ推定で共分散行列の事前分布は逆ウィシャート分布とするのが定番だが、お兄さんがた、ほんとにそれでいいと思うのかい？ という論文。SEM-NETで紹介されていて、仕事と関係する話ではあるので、ざっと目を通した次第。

　ベクトル$Y_i$ ($i=1, \ldots, n$)がiidに$N(\mu, \Sigma)$に従う、というMVNなモデルを考える。$\Sigma$は$d$次元の正定値行列。
　データ全体を$y$として、その尤度は
　$\displaystyle p(y | \mu, \Sigma) \propto |\Sigma|^{-n/2} \exp \left( -\frac{1}{2} tr(\Sigma^{-1} S_\mu) \right)$
である。ただし$S_\mu = \sum^n_i(y_i-\mu)(y_i-\mu)^T$。

　さて、共分散行列$\Sigma$の事前分布をどうするか。ふつうは自然共役事前分布である逆ウィシャート(IW)分布を使うところだが、ここではその他に、scaled IW分布, 階層IW分布, 分離方略を紹介しよう。

　事前分布その1, IW分布。
　$\displaystyle p(\Sigma) \propto |\Sigma|^{\frac{\nu+d+1}{2}} \exp(-\frac{1}{2}tr(\Lambda \Sigma^{-1}))$
ここで$\Lambda$は$d$次元の正定値行列, $\nu$は自由度で、$\nu > d-1$のときにproper。平均は$\nu > d+1$のときに $\Lambda / (\nu-d-1)$である。ふつうは$\Lambda=I, \nu = d+1$とする。こうするとすべての相関の周辺分布が一様になる。[←このくだり、全く意味を考えず虚心に写経している。だって、らららー、文系なんだものー]
　その共役性によって広く愛されているIW分布だが、欠点が３つある。

　事前分布その２、scaled IW(SIW)分布。えーと、これはですね、要素$\delta_i$を持つ対角行列$\Delta$について$\Sigma \equiv \Delta Q \Delta$としてですね、
　$Q \sim IW(\nu, \Lambda)$
　$\log(\delta_i) \sim N(b_i, \xi_i^2)$ (iidで)
とするわけです。要するに変数ごとに分散を変えられるわけね。

　事前分布その３、階層Half-t分布。まず
　$\Sigma \sim IW(\nu+d-1, 2\nu\Lambda)$
とする。ここで$\Lambda$は対角行列で、その要素を
　$\lambda_i \sim Ga(1/2, 1/\xi_i^2)$ (iidで)
とするんだそうです。なんだかさっぱりわからん。これはSDの事前分布をhalf-t分布にしていることになる由。なんだかさっぱりわからん。(繰り返し)

　事前分布その４、分離方略。
　$\Sigma \equiv \Lambda R \Lambda$とする。$\Lambda$は要素$\sigma^i$を持つ対角行列で、SDの事前分布。$R$は要素$\rho_{ij}$を持つ相関行列。とこのように分離しておいて、別々に事前分布を与える。ああそうか、SDと相関を別々にモデル化するのか。
　相関のほうは、$R=\Delta Q \Delta$とし($\Delta$は対角行列で... 詳細省くけど、$Q$をうまいこと相関行列に変換するという主旨だと思う)、$Q \sim IW(\nu, I)$とする。で、$\log(\sigma^i)$はiidに$N(b_i,\xi_i)$に従うものとする。
　なんでこれを取り上げるかというと、これがStanのオススメだから。

　...なんだか関心がなくなっちゃったので(「能力が及ばない」の婉曲表現)、シミュレーションと実例をパスして一気に結論に飛ぶと...

というわけで、Stanをお使いの場合は分離方略がオススメ。でも計算が大変だったり無理だったりする場合、もし相関が推定できるだけでいいってんなら、あらかじめデータを分散1にしておいてIW分布を使うのがよろしい。とのこと。

　...いやー、正直わたくし仕事ではMplus一択、よって共分散行列の事前分布はIW一択なんだけど、こうしてみると、Mplusではやっぱ事前のスケーリングが大事ってことやね。Muthen導師の日頃のご託宣のとおりである。南無南無。

論文：データ解析(2015-) - 読了：Alvarez, et al. (2014) 共分散行列の事前分布は逆ウィシャート分布でいいのか

溜まった論文メモをちびちびアップ中。まだ5月分だ。なかなか片付かない...

Little, T.D., Slegers, D.W., Card, N.A. (2006) A non-arbitrary method of identifying and scaling latent variables in SEM and MACS models. Structural Equation Modeling, 13(1), 59-72.

　多群のSEMモデルでモデル識別のために制約を掛けるとき、因子分散を1にするのでもなければ最初の指標の負荷を1にするのでもない、新しい制約の掛け方をご提案します。それはeffect-codingです！ という論文。仕事の都合で読んだ。

　準備。
　$X$を長さ$p$の観察ベクトルとし、その平均ベクトルを$\mu$, 分散共分散行列を$\Sigma$とする。群$g=1, \ldots, G$があり、群$g$に属する観察ベクトルを$X^g$とする。次のモデルを考える。
　$X^g = \tau^g + \Lambda^g \xi^g + \delta^g$
$\tau^g$は長さ$p$の切片ベクトル、$\Lambda^g$は$(p \times r)$の負荷行列, $\xi^g$ [原文には$\chi^g$という表記も混在している] は長さ$r$の潜在ベクトル、$\delta^g$は長さ$p$の独自因子ベクトル。平均構造と共分散構造は
　$\mu^g = \tau^g + \Lambda^g \kappa^g$
　$\Sigma^g = \Lambda^g \Phi^g \Lambda^{g'} + \theta^g$
$\kappa^g$は長さ$r$の潜在変数平均ベクトル, $\Phi^g$は$(r \times r)$の潜在変数共分散行列、$\theta^g$[$\theta^g_\delta$という表記も混在している]は独自因子の分散を表す$(p \times p)$の対角行列である。
　以下のように仮定する。$E(\delta)=0$。$Cov(\delta\delta')=0$。独自因子と共通因子は独立。観察変数と独自因子はMVNに従う。
　測定モデルは本質的同族(essentially congeneric)と仮定する。つまり、所与の潜在変数の指標の切片$\tau$についても、所与の潜在変数の指標$\lambda$についても、独自分散$\theta$についても制約しない、広い範囲の測定モデルについて考える。というか、測定不変性の制約をどこまでかけるか、それをどうやって決めるかは、この論文のテーマではない。この論文が問題にするのは、モデル識別のための制約をどうやってかけるか、である。

　本題。
　モデル識別のための制約のかけかたが3つある。

　方法1: 参照群法。
　群1の潜在変数平均ベクトル$\kappa^1$を0に固定し、群1の潜在変数共分散行列$\Phi^1$の対角要素を1に固定する。負荷$\Lambda^g$と切片$\tau^g$に群間等値制約をかければ、潜在変数の平均と分散は群2以降で自由推定できる。
　このとき、$\tau$は群1の平均の推定になる。群2以降の潜在変数平均ベクトル$\kappa^2, \ldots, \kappa^G$は、その潜在変数の指標群の平均差を負荷で重みづけたものとなる。
　また、個々の潜在変数の負荷$\lambda$は、群1での負荷となる。群2以降の潜在変数分散$\Phi^g$は、その潜在変数で説明された共通分散を比で表したものになる。

　方法2: マーカー変数法。いうならば、切片・負荷のdummy-codingである。
　個々の潜在変数について、その(たとえば)最初の指標を選んで、その切片$\tau^g_{1r}$を0に固定し、負荷$\lambda^g_{1r}$を1に固定する。残りの負荷と切片には群間等値制約をかける。この方法は、潜在変数のスケールを最初の指標に合わせたことになる。選ぶ指標は別にどれでもよい。ふつうはどの指標を選んでも適合度は変わらない。(ただし、すごく無制約なモデルは例外で...と、Millsap(2001 SEM)を挙げている。これ、どっかで聞いたことがあるなあ...)

　方法3: effect-coding法。
　個々の潜在変数について、指標の切片の和を0、負荷の平均を1と制約する。つまり、潜在変数$r$の指標の数を$I$として
　$\sum_i^I \lambda^g_{ir}=I, \ \ \sum_i^I \tau^g_{ir} = 0$
これだけでもモデルは識別できる。この方法だと、潜在変数の分散は、その潜在変数で説明された分散の重みつき平均となり、潜在変数の平均は、その潜在変数の指標の平均の重みつき平均となる。その重みが合計1になるように最適化されているわけである。

　計算例...[略]

　比較すると、

　なお、以上の3種類でモデルの適合度は変わらないし、潜在変数の差の効果量も変わらない。
　
　なお、ここまで多群モデルについて考えてきたが、この話は縦断モデルにも適用できる。
　以上の議論は単純構造がある場合の話で、交差負荷がある場面については今後の課題である。云々。

　... なぜこの論文を読んでいるのか途中から自分でもよくわかんなくなっちゃったんだけど、ま、勉強になりましたです。
　多群SEMでeffect-codingしたくなる状況ってのがいまいちピンときてないんだけど、たとえば全指標の尺度が同じで、交差負荷のないCFAで、かつ切片と負荷の群間等値制約を掛けている(ないし、その指標についても外している)ような場面では、それはわかりやすいかもなと思う。もっとも、たとえば測定の部分不等性を捉えるために、一部の指標についてだけ負荷の等値制約を外しているような場面では、いくら適合度は変わらないといえ、負荷の平均を1に揃えるというのはなんだか奇妙な話だと思う。
　ま、いずれ使いたくなる場面に出くわすかもしれないな。覚えておこう。

　ところで、我らがMplusはどうなっているかというと... 私の理解が正しければ、Mplusのデフォルトは、
　「因子負荷は最初の指標で1に固定、切片は定数制約なし、因子平均は第1群で0に固定、因子分散は制約なし、指標の切片と因子負荷は群間等値」
なので、参照群法とマーカー変数法の中間といったところ。もちろん、参照群法、マーカー変数法、effect-coding法のいずれのモデルも組めるはずである。

論文：データ解析(2015-) - 読了：Little, Slegers, Card (2006) 潜在変数モデルを識別するためのeffect-coding制約

論文メモの記録。まだ5月分だ...

Loffler, M. (2014) Measuing willingness to pay: Do direct methods work for premium durables? Marketing Letters, 26, 535-548.
　支払意思額(WTP)の聴取方法を比較した研究。PSM(price sensitivity meter)とCBC(選択型コンジョイント)を比べる。著者の所属はポルシェだそうである。

　いわく。
　WTP測定には、PSMのような直接法と、コンジョイント分析のような間接法があって、往々にして結果が違う。Steiner & Hendus (2012, WorkingPaper)の調査によれば、ビジネスでは直接法のほうが良く使われている(全体の2/3)。
　WTP聴取方法を比較した先行研究をみると[...5本の論文を表にして紹介...]、消費財・サービスが多く、被験者は学生が多く、文化差研究がみあたらない。

　仮説。自動車で実験します。

[結果次第であとからなんとでもいえる話ばかりで、いささか萎える。わざわざこういう仮説検証研究的なしぐさをしなくてもいいじゃんと思うのだが、まあ、この領域のお約束なのであろう...]

　実験。
　US, ドイツ, 中国でやった高級車の「カークリニック」で実験した。[←前職で初めて知ったのだが、調査会場で新車(ないしそのモック)を提示する消費者調査のことを「クリニック」と呼ぶ。車検のことではない。たぶん自動車業界に特有な用語だろう(白物家電の「クリニック」って聞いたことがない)。面白い業界用語だなあと思う。誰が医者で誰が患者なんでしょうね]
　対象者は過去4年以内新車購入者で高年収で次回購入車を決めてない人, 各国約500人強で計1640人。新車と競合車(BMWとかMBとか)、計7台を提示。
　いろいろ訊いた後にPSM(4問のうち「安い」設問を特売価格のストレート設問とみなす)、市場価格ストレート設問(「割引がないとしていくらだと思います？」)、CBC課題。[順序が書いてないぞ。カウンターバランスしてないとか？]
　CBCは、属性は(1)メークとモデル、(2)エンジンタイプ, (3)馬力、(4)国産/輸入, (5)装備、(6)価格。それぞれ3～4水準。12試行、1試行あたり7台+「どれも選ばない」から選択。ホールドアウトは調べてないが、NCBS調査と照合して妥当性を検証しました、云々。[NCBS調査とは欧州車を中心とした新車購買者調査のこと]

　結果。
　H1, H2を支持。わざわざPSMで受容価格帯を調べなくても、ストレート設問の集計と変わらない。
　CBCの各選択肢のコストを別のデータから調べておいて、利益を最大化する価格を求めた。これをPSMの最適価格点と比べると、後者のほうが低い。[モンテカルロ法で幅を出して... 云々と説明があるが、省略]。H3を支持。
　国によるちがいは...[めんどくさくなってきたのでスキップ]

　考察。高級耐久財でWTPの実験をやりました。手法は選ばなあきませんね。ちゃんと国別に調べんとあきませんね。云々。

　わざわざ読まなきゃいけないほどの話じゃなかったけど(すいません)、PSMについてきちんと実験している研究はあまり多くないので、えーと、その意味ではですねー、参考になりましたですー。
　それにしても... ちょっとこらえきれないので書いちゃうけど、PSMの最適価格点と、CBCの最適価格点を比べるのは、いくらなんでも無理筋でしょう。PSMは(妥当かどうかは別にして)消費者の価格知覚からみた最適価格を調べようとしているのに対して、CBCの最適価格点とはメーカーからみた利益最大化価格である。もしメーカーがPSMの最適価格で値付けしちゃったら、売上がどうなるかは知らないが、利益が最大化されないのは当っっったり前であろう。いったいなにを考えておられるのか。まあいいけどさ。

　話はちがうが：
　PSMの設問文については前に論文や書籍を調べたことがあるんだけど、4問の設問で毎回「品質」という言葉を使い、思い切り知覚品質にフォーカスした設問文を採用している人と(Monroe(2003), 杉田・上田・守口(2005)など)、「品質」という言葉をあまり使わず、単に安すぎ/安い/高い/高すぎな価格を訊く方向の人(Travis(1982), 朝野・山中(2010)など)がいると思う。この論文の設問文は後者の路線。この違いって、歴史的には何に由来してるんですかね。

論文：調査方法論 - 読了：Loffler (2014) 高級車の消費者支払意思額をPSMとコンジョイント分析で比較する

2017年8月24日 (木)

引き続き、論文のメモを記録しておく。このへんまで、たぶん５月頃に読んだ奴だと思う。

Agresti, A. (1992) Analysis of Ordinal Paired comparison Data. Journal of the Royal Statistical Society. Series C (Applied Statistics), 41(2), 287-297.
　先日読んだレビュー論文で、一対比較への段階反応データについての隣接カテゴリロジットモデルというのが紹介されていて、よく意味がわからなかったので、引用文献を辿って読んでみた。

　いわく。
　処理$h$と$i$を比べたとき、$i$が選好されることを$Y_{hi}=1$, $h$が選好されることを$Y_{hi}=2$とする。Bradley & Terry (1952)のモデルは
　$\displaystyle \log \frac{P(Y_{hi} =1)}{P(Y_{hi} =2)} = \mu_i -\mu_h$
で、これは
　$\displaystyle P(Y_{hi}=1) = \frac{\exp(\mu_i)}{\exp(\mu_i)+\exp(\mu_h)}$
とも書ける。このへんの歴史に関心をお持ちの向きはDavid(1988, 書籍)あたりを見るがよろしい。
　さて、BTモデルをタイあり比較(つまり3件法)へと拡張する試みは60年代からある。では、これを5件法とか7件法とかに拡張する方法について考えよう。

　処理の数を$I$, 順序反応カテゴリ数を$J$とする。処理$h$と$i$を比べた反応を$Y_{hi}$とする。尺度は対称だ ($Y_{hi}=j$なら$Y_{ih}=J-j+1$だ) と仮定する。

　その1, 累積リンクモデル。
　連続潜在変数$Y^*_{hi}$と、それを反応$Y_{hi}$に変換するための閾値$\alpha_1, \ldots, \alpha_{J-1}$ (小さい順) を考える。さらに、処理への潜在的評価$Y_h, Y_i$を考え、$Y^*_{hi} = Y_h - Y_i$と考える。そして、各処理の効用パラメータ$\mu_i, \mu_h$を考え、$Y_h-\mu_h, Y_i-\mu_h$は比較によらず同一の分布にしたがうと考える。すると、
　$Z = (Y_i - \mu_i) - (Y_h - \mu_h)$
は比較によらず同一の分布に従い、
　$\alpha_{j-1} - (\mu_h - \mu_i) < Z < \alpha_j - (\mu_h - \mu_i)$
のときに$Y_{hi}=j$だってことになる。$Z$の累積分布関数を$F$とすれば
　$F^{-1}(P(Y_{hi} \leq j)) = \alpha_j - (\mu_h-\mu_i)$
である。
　$F^{-1}$をロジットリンクにすると、$J=2$ならばBradley-Terryモデルになる。$F^{-1}$をプロビットリンクにすると、$J=2$ならばThurstone-Mostellerモデルとなる。

　その2、隣接カテゴリロジットモデル。
　反応$j$と$j+1$にだけ注目する。上記と同様に、反応は$Z+\mu_i-\mu_h$で決まっているのだと考えて
　$\displaystyle \log \frac{P(Y_{hi}=j)}{P(Y_{hi}=j+1)} = \alpha_j - (\mu_h -\mu_i)$
これを書き換えると
　$\displaystyle \frac{P(Y_{hi}=j)}{P(Y_{ih}=j)} = \exp((J+1-2j)(\mu_h -\mu_i))$
つまり、たとえば7件法だとして、$\exp(2(\mu_i-\mu_h))$は回答3 vs 5のオッズ、その2乗は回答2 vs 6のオッズ, 3乗は1 vs 7のオッズだということになる。累積リンクモデルより解釈しやすい。

　... ここからは、推定方法の話、事例、比較に独立性がない場合の話。読みたいところが終わっちゃって急速に関心が薄れたので、パス。

　なあんだ、隣接カテゴリロジットってそういう話か、と納得したのだが(隣接する2カテゴリの下での条件付き確率のロジットを効用の線形関数とみるわけね。結局ベースライン・カテゴリを決めたロジットモデルと同じことだ)、Agrestiの分厚い本を見たら、順序カテゴリデータの章にちゃんと書いてあった。なんだかなあ。手持ちの教科書をちゃんと読めという話である。

　素朴な疑問なのだが... 消費者調査で、刺激セットの総当たり対について選好判断を繰り返すとき、恒常和法で聴取することがある。ここに(たとえば)10枚のチップがあるとして、好きなほうにより多くのチップを置いてください、という訊き方である。
　テクニカルにいえば、この回答は刺激対に対する0～11の11件法評定だと考えて分析することもできるし、独立に行った10回の試合の勝敗集計だと捉えて、ThurstonモデルなりBradley-Terryモデルなりを当てはめることもできる(そういう事例を見たことがあるし、ここだけの話、自分でもやったことがあります)。でも正直なところ、後者のアプローチにはかなり抵抗がある。あるペアに対するチップの置きかたが、あるパラメータの二項分布に従っていると考えていることになるわけで、ちょっと仮定が強すぎるように思うわけである。
　でも考えてみると、チップの置きかたを11件法評定だと捉えて累積リンクモデルなり隣接ロジットモデルなりを当てはめたとしても、それはそれで強い仮定が置かれている。どちらのモデルでも閾値は左右対称だし、$Z$(効用の差と潜在評価の差とのずれ)にはなんらかの確率分布が仮定されている。つまり、あるペアに対するチップの置きかたが、あるパラメータの正規分布だかなんだかに従っていると考えているわけで、結局のところ五十歩百歩なんじゃないかしらん。
　実のところ、10枚のチップの置きかたと効用差との関係は、回答生成の心的過程に関わる実質的な問題で、心理実験で調べるべき問題なんじゃないかと。そういう研究があるといいんだけどなあ。

論文：データ解析(2015-) - 読了：Agresti(1992) 一対比較への順序尺度型回答を分析するための2つのモデル

　仕事の都合でBradley-Terryモデルを使っていて(←そういう古典的モデルがあるのである。大儲けとはおよそほど遠い地味な分野の地味な話題なのである。世のデータサイエンティストたる皆様はもっと他の金になる話について知識を誇ったほうがよいだろう)、これって学部生のときに習ったサーストンのモデルと実質的にどうちがうんだろう？(←そういう超古典的なモデルがあるのである。計量心理の先生がなぜかそういう黴臭い話を延々と続けて止まなかったのである。もっと他の話をしてくれりゃよかったのに)、とふと疑問に思ったので、適当に検索して、出てきた魅力的な感じのPDFを印刷して、筒状に丸めて片手に持って外出した。
　で、移動中にパラパラめくったら、これは... 俺の読みたかった話と違う... いや、まあ、いいけどさ...

　Stern, H. (1990) A continuum of paired comparisons model. Biometrika, 77(2), 265-73.
　というわけで、途中からうとうとしながらパラパラめくっただけだけど、一応メモ。
　既存の一対比較モデルを、ガンマ確率変数を使ったモデルで包括的にご説明します、という話。

　$k$個の刺激(プレイヤー)のトーナメント戦について次のように考える。
　プレイヤー$i$のスコアは率$\lambda_i$のポワソン過程に従い、スコア獲得のプロセスはプレイヤー間で独立とする。2個のプレイヤーの勝敗とは「どっちが先にスコア$r$を獲得するか」であるとする。[←なんというか、一対比較課題への回答を生成する認知モデルとしては非常にナンセンスな気がするが、そういうご主旨の論文ではないのだろう]。
　このとき、プレイヤー$i$がスコア$r$を獲得するまでにかかる時間は、形状$r$, スケール$\lambda_i$のガンマ分布に従いますね。$i$が$j$に勝つ確率を$p^{(r)}_{ij}$は、形状はどちらも$r$でスケールは$\lambda_i, \lambda_j$である2つの独立なガンマ確率変数$X_i, X_j$を考えると
　$p^{(r)}_{ij} = pr(X_i < X_j)$
中略するけど、これは結局
　$\displaystyle p^{(r)}_{ij} = f(r, \frac{\lambda_i}{\lambda_j})$
と書ける[← 原文には$f$の中身が書いてあるけど面倒なので省略]。

　このガンマ確率モデルの枠組みで、既存のいろんなモデルを扱える。
　たとえば$r=1$とすると、これは
　$\displaystyle p^{(r)}_{ij} = \frac{\lambda_i}{\lambda_i + \lambda_j}$
となる由。この系統のモデルはいっぱいあって(convolution type linear model)、Bradley-Terryモデルもそのひとつ。
　また、たとえば$\displaystyle \frac{\lambda_i}{\lambda_j} = \frac{1}{1+\Delta r^{-1/2}}$とすると、これは
　$\displaystyle \lim_{r \to \infty} p^{(r)}_{ij} = \Phi \left( \frac{\Delta}{\sqrt{2}} \right)$
となる由。ただし$\Phi(\cdot)$は標準正規分布の積分。これはThurstone-Mostellerモデルに近い。[...後略...]

　データへの適合度でモデルを比較してもいいけど、$n$がすごく大きくない限りどっちもみな様な結果になるのよ。昔の研究で、Bradley-TerryモデルでもThurstone-Mostellerモデルでもデータへの適合は似たようなもんだという指摘が多いが、それはこういうことなのよ。云々。

論文：データ解析(2015-) - 読了：Stern(1990) 一対比較データを扱ういろんなモデルを「2つの刺激がそれぞれ謎の得点を稼いでいきある得点に先に達したほうの刺激が勝つのだ」モデルで包括的に説明する

2017年8月23日 (水)

　これも仕事の都合で、かなり前に読んだ奴。

Cattelan, M. (2012) Models for paired comparison data: A review with emphasis on dependent data. Statistical Science, 27(3), 412-433.

　一対比較データのためのモデルに関する、全21頁のレビュー。著者はイタリアのポスドクさん。題名にある dependent dataとは、比較と比較の間に独立性がない、という意味。

　対象者$s$が対象$i$と$j$を比較した値を$Y_{sij}$とする。当面、観察は独立と考える(たとえば、ある対象者はひとつの比較しかしないものとする)。

　その1, 伝統的モデル。
　伝統的なモデルでは、$Y_{sij}$は二値で、$i$が勝つ確率$\pi_{ij}$は対象の効用$\mu_i, \mu_j$の差の関数、すなわち
　$\pi_{ij} = F(\mu_i - \mu_j)$
である。これをunstructured modelという。$F$が正規累積分布ならThurstone(1927)のモデルとなり、ロジスティック累積分布ならBradley-Terryモデル(1952)となる。モデルの目的は効用ベクトル$\mathbf{\mu} = (\mu_1, \ldots, \mu_n)'$についての推論である。なお識別のためになんらかの制約をかける必要がある。和が0だとか。
　普通は効用の差に関心があるわけだけど、そうすると次の問題が起きる。たとえば$H_0: \mu_i = \mu_j$をワルド統計量$(\hat{\mu}_i - \hat{\mu}_j)/\sqrt{\hat{var}(\hat{\mu}_i-\hat{\mu}_j})$で検定したいとするじゃないですか。$\hat{\mu}_i$と$\hat{\mu}_j$は独立じゃないから共分散が要る。でもいちいちめんどくさい。そこで擬似分散を使うことが多い。[... 共分散が正なら分散を割り引くという話。考え方が説明されているんだけどよくわからなかった。Firth & de Menezes (2004, Biometrika)を読めとのこと]

　その2, 順序型の一対比較。
　たとえば、タイを許す比較とか、「どちらともいえない」を真ん中にとった5件法とか。
　Agresti(1992, JRSS)は2つモデルを挙げている。ひとつめ、累積リンクモデル。
　$pr(Y_{ij} \leq y_{ij}) = F(\tau_{y_{ij}} - \mu_i + \mu_j)$
として、累積ロジットモデルだか累積プロビットモデルだかに持ち込む。
　ふたつめ、隣接カテゴリモデル。[説明が書いてあったんだけどよくわからなかった。3件法なら、回答(1,2)だけのロジスティック回帰モデルと回答(2,3)だけのロジスティック回帰モデルを推定する、ということ？ まさかねえ...]

　その3, 説明変数の導入。
　たとえば、対象についての説明変数を導入して
　$\mu_i = x_{i1} \beta_1 + \cdots + x_{iP} \beta_P$
とか(もちろん対象固有な切片をいれてもよい)。こういうのをstructured modelという。ただの線形結合じゃなくて、たとえばスプライン・スムーザーの線形結合にしましょうなどという提案もある。
　対象者についての共変量を入れるという提案もある。また、対象者の潜在クラスを考えるという提案もある(Dillon, Kumar, & de Borrero, 1993 J.MktgRes)。[←直感として、そのモデル、Mplusで組めちゃいそうだなあ...]
　対象者を共変量で再帰分割しながらBradley-Terryモデルを推定しまくるという提案もある。[変態だ、変態が現れた... Strobl, Wickelmaier, Zeileis (20011, J.Edu.Behav.Stat.)だそうだ]
　個々の比較についての共変量を入れるという提案もある。スポーツのホーム・アドバンテージとか。

　ここからは、独立性がないデータのためのモデル。

　その4. 推移律が成り立たないモデル。
　効用を多次元化して捉えようというモデルとか(最終的なランキングは出せないことになる)、比較の間の従属構造を考えるモデルとかがある。

　その5. 一人の対象者が複数の比較をするモデル。
　これは研究が多い。

　アプローチ1, サーストン・モデル。もともとThurstone(1927)は知覚弁別について考えていたわけだが、そもそも彼にとって$n$個の刺激$(T_1, \ldots, T_n)'$は多変量正規分布に従うのであり、つまり刺激は共分散を持つのである。またTakane(1989)のモデルは、それぞれの比較に誤差を持たせ、その誤差に共分散を持たせており、そのおかげでwandering vectorモデル, wandering ideal pointモデルを扱うことができる[←よくわからんが、効用が共分散行列を持つだけじゃなくて比較が共分散行列を持っているから、たとえばなにとなにを比べるかによって理想ベクトルが切り替わっちゃうようなデータ生成構造が表現できたりする、ということだろうか]。
　こういうモデルはパラメータがめっさ多くなるのでなんらかの制約が必要である。サーストンは刺激の共分散行列に制約を掛けたし、Takaneは因子モデルを使った。
　もっと拡張したモデルにTsai & Bockenholt (2008)というのがあってだね...[略]
　計量心理学者が関心を持つのは刺激の間の関係なので、最大の関心はunstructuredで無制約なサーストンモデルにあるんだけど[←なるほどね]、残念ながらなんらかの制約が必要である。Takaneが考えたような個々の比較が誤差を持つモデルを識別するためには、最低限どんな制約が必要かといいますと...[ああ、面倒くさい話だ... パス]

　アプローチ2, ロジット・モデル。最初期はLancaster & Quade (1983)というので、効用をベータ分布に従う確率変数と捉えた。でも「同じ対象者における同じ対象ペアの比較」のあいだに相関を導入しただけだった。
　オッズ比を使うアプローチもある。普通の統計ソフトで推定できるのが長所。[←短い説明があるんだけどさっぱりわからん]
　対象の効用にランダム効果をいれるというアプローチもある[←っていうか、普通そういう風に考えません？]。たとえば、個人$i$, 対象$i$について
　$\mu_{si} = \mu_i + \sum_p \beta_{ip} x_{ip} + U_{si}$
とか。Bockenholt(2001, Psych.Method)など。

　アプローチ3, 経済学における選択モデル。この文脈では、ランダム効用モデルのIIA仮定をどうやって緩和するかという点が問題になっていた。nested logitモデルとか、効用に乗っている個人別の誤差に共分散を考える多変量プロビットモデルとか。
　経済学における選択理論の特徴は、調査票で調べるstated preferenceと選択課題で調べるrevealed preferenceを別物として扱うという点である。両方を同時に扱うモデルとしてWalker & Ben-Akiva (2002 Math.Soc.Sci.)がある。[←へー]

　その6. 対象に関連した依存性があるモデル。
　たとえば動物のあいだのコンテストで、固有の個体がランダム効果を持つ、というような場合。[へー、そんな問題があるのね。でも関心ないのでパス]

　さて、上記その5のような、独立性のないデータのためのモデルをどうやって推定するか。[... ここから、どんな尤度をどうやって求めるか、適合度をどうやって測るのか、というような難しい話に突入し、おおこれは統計学の論文だったのか、と思い出した次第。5頁にわたってスキップ。どうもすいません]

　最後にRのパッケージ紹介。

最後のまとめのところに今後の課題がいろいろ書いてあったけど、疲れたのでパス。

論文：データ解析(2015-) - 読了：Cattelan (2012) 一対比較データのための統計モデル・レビュー

Austin, P.C., Jembere, N., Chiu, M. (2016) Propensity score matching and complex survey. Statistical Methods in Medical Research.
　先日目を通したRidgeway et al.(2015)に引き続き、「標本ウェイトつきのデータで傾向スコア調整するときどうするか」論文。シミュレーションしましたという話である。

　この論文は前置きをすっ飛ばしてシミュレーションの設定をみたほうがいいと思うので(というか誠実に読むにはいささか疲れてるので)、いきなりシミュレーションについてメモする。

　層別クラスタ抽出の場面を考える。母集団は、層10, 各層に20クラスタ、各クラスタに5000人、計100万人。
　データを生成する。共変量は6個。共変量$l$について、層$j$はランダム効果
　$u^s_{l,j} \sim N(0, \tau^s_l)$
を持ち、クラスタ$k$はランダム効果
　$u^c_{l,k} \sim N(0, \tau^c_l)$
を持ち、各ケースは値
　$x_{l,ijk} \sim N(u^s_{l,j}+u^c_{l,k}, 1)$
を持つ。
　処理を割り当てる。処理は2値とし、処理群における確率$p_i$を
　$logit(p_i) = a_0 + a_1 x_1 + a_2 x_2 + \cdots + a_6 x_6$
として、処理変数を
　$Z_i \sim Be(p_i)$
とする($Be$はベルヌーイ分布ね)。回帰係数は, $a_1 = \log(1.1), \ldots$という風に固定。
　2つのアウトカムを生成する。ひとつは量的変数で、めんどくさいから式は省略するけど、要するに6個の共変量と正規誤差と定数の線形和で、処理群に限り、さらに定数と共変量のうち3つの線形和が乗る。係数はみな固定である。もうひとつは二値変数で、これも$logit(p_i)$を同じようにつくっておいてベルヌーイ分布で生成。
　こうして、母集団ができました。以下、estimandはPATT (母集団のATT) とする。

　さあ抽出しましょう。
　標本サイズは全部で5000。この層への配分がちょっとわからなくて...

We allocate samle sizes to the 10 strata as follows: 750, 700, 650, 600, 550, 450, 350, 300, 250, where the sample size allocated to each stratum was inversely proportinal to the cluster-specific random effect used in generating the baseline covariates. Thus, disproportionately more subjects were allocated to those strata within which subjects had systematically lower values of the baseline covariates, while disproportionately fewer subjects were allocated to those strata within which subjects had systematically higher values of baseline covariates. This was done so that structure of the observed sample would be systematically different from the population from which it was drawn.

　要するにアウトカムと抽出確率を相関させたということなんだろうけど(無相関ならウェイティングする意味が薄れるから)、そのやり方がわからない。cluster-specific random effectは全層を通して平均ゼロの正規分布に従うんでしょうに。ひょっとして、200個のランダム効果$u^c_{l,k}$を生成したあとで層別に平均し、値が小さい層から順に標本サイズを750, 700, ... と割り当てていったということだろうか。だとしたら、6個の共変量をどうやってまとめたんだろうか。ひょっとして、アウトカムを生成する式でつかった係数で線形和をとったという話だろうか。よくわからん。まあいいけどさ。
　各層あたり5クラスタを単純無作為抽出し、標本サイズを各クラスタに均等に割り当てて無作為抽出する。

　傾向スコアを求めましょう。
　３つのモデルを試す。どのモデルも、6個の共変量を使ったロジスティック回帰で推定する。
　モデル1, 標本ウェイトを使わない。
　モデル2, 標本ウェイトを使った重みつきロジスティック回帰。
　モデル3, 6個の共変量に加えて標本ウェイトを投入したロジスティック回帰。

　マッチングしましょう。(そうそう、そうなのだ、書き忘れていたがこの論文は傾向スコアでマッチングするときにどうするかという論文なのだ。あれ、なんでいまこんなの読んでいるんだっけ？ 当面マッチングする用事はないんだけどなあ...)
　層やクラスタは忘れて傾向スコアのロジットだけを使い、greedy NNMを使って(えーと、最近傍マッチングのことね)、2群の対象者をマッチングする。キャリパーは0.2SDとする。greedy NNMはただのNNMや最適マッチングよりも優れていることが知られている(Austin, 2014 Stat Med.というのが挙げられている。どう違うのか知りませんけど、信じますよ先生)
　
　PATTを推定しましょう。２つの方法を試す。
　方法1, natural weight。マッチした標本について、群ごとに標本ウェイトで重みづけた平均を求め、その差を求める。
　方法2, inherited weight。マッチした標本のうち統制群側の対象者のウェイトを、その相方である処理群の対象者のウェイトにすり替えたうえで、推定1の方法を用いる。
　どちらについてもブートストラップ法でSEを推定する (詳細はパス)。

　... 問題設定はよくわかったので(そして疲れてきたので)、シミュレーションの詳細はパス(2つの$\tau$を動かしていくつかシナリオをつくったらしい)。手法評価の詳細もパス(PATT推定の分散とバイアスを評価するんだと思う)。感度分析もパス。結果についてのみメモする。
　
　共変量のバランスはどのくらい実現されたか。natural weightだときれいにバランシングされ、inherited weightでは少しインバランスが残る(その差は層による分散が大きいときに大きくなる)。傾向スコアモデルを問わずそうなる。
　PATT推定のバイアスはどうなったか。natural weightでバイアスはほぼゼロ、inherited weightで大きいほうに偏る(その差は層による分散が大きいときに大きくなる)。傾向スコアモデルを問わずそうなる。
　PATT推定のMSEはどうなったか... 信頼区間はどうなったか... (面倒になってきたのでパス)

　後半はケーススタディ。疲れたのでまるごとパス。

　考察。
　３つの傾向スコアモデルのうちどれがいいとはいえない。
　マッチング後の集計の際、標本ウェイトはnatural weightにしたほうがよい。

　... 肝心の「傾向スコアモデルに標本ウェイトを使うか」問題は、どれがいいのかわからんという結論になってしまった模様。おいおい、せっかく読んだのにそりゃないよ、と思ったんだけど、まあ実際そうなんでしょうね。だいたいさ、まともな標本抽出デザインならウェイティングしようがしまいが回帰モデルなんてそうそう変わらないし、変わるようなデザインだったらウェイティングするの怖いですよね。結局ウェイティングなんて気分の問題なんですよね。僕らの仕事なんて所詮そんなものなんですよね。いいんだどうせ僕なんか。いっそ死ぬまで寝ていたい。(すいません疲れているんです)
　マッチング後は各群を素直にウェイティングしたほうが良いという話、そりゃそうだろう、むしろinherited weightなんていう発想がわからないよ、と思ったんだけど、きっとそれにはそれで筋道があるんでしょうね。でもこの話、マッチング後の集計の話であって、もはや傾向スコアと関係なくないっすかね。

論文：データ解析(2015-) - 読了：Austin, Jembere, Chiu (2016) 層別クラスタ抽出標本の2群を傾向スコアでマッチングするとき傾向スコアの算出に標本ウェイトを使うべきかどうか調べてみたけどよくわかんなかった

2017年8月22日 (火)

McCaffrey, D.F., Griffin, B.A., Almirall, D., Slaughter, M.E., Ramchand, R., Burgette, L.F. (2013) A tutorial on propensity score estimation for multiple treatments using generalized boosted models. Statistics in Medicine, 32, 3388-3414.
　題名の通り、処理が3水準以上あるときに、generalized boosted modelを用いて傾向スコア調整するやり方についての長ーいチュートリアル。著者らはRのtwangパッケージの中の人。急遽実戦投入を迫られ、事前の儀式としてめくった。

　処理の水準数を$M$ とする。ある人が処理 $t$ を受けた時のpotential outcomeを$Y[t]$ とする。ペアワイズの効果を$D[t', t''] = Y[t'] - Y[t'']$と書く。
　因果的効果についての統計量として次の2つを考える。

$M=3$の場合、ATEは3つ、ATTは6つあることになる。
　ATEとATTのちがいは、対象者間の効果の異質性から生まれる。[←あっ、そうか。効果がhomogeneousだったらどちらでも同じことだわな。なるほど...]
　どういうときにどっちのestimandが適切か？　すべての処理が潜在的には母集団全員に適用可能なのであれば、ATEが自然。いっぽう、処理$t'$が現在のターゲットに対して適切なものかどうかに関心があるのならATTが自然。

　いよいよ本題。どうやって推定するか。
　個人$i$について、観察された処理を$T_i$、観察されたアウトカムを$Y_i$、共変量のベクトルを$\mathbf{X}_i$とする。
　ここではIPTW (inverse probability of treatment weighting) 推定量について考えよう。この推定量は2つの想定を置く。どちらもデータからは検証できない想定である。

　さて、$p_t (\mathbf{X}) = pr(T[t] = 1 | \mathbf{X})$を傾向スコアと呼ぶ。
　上の2つの想定の下で、
　$\displaystyle \hat{\mu}_t = \frac{\sum_i T_i[t] t_i w_i[t]}{\sum_i T_i[t] w_i[t]}$
は$E(Y[t])$の一致推定量になる。ただし$w_i[t]$とは傾向スコアの逆数、すなわち$w_i[t] = 1 / p_t(\mathbf{X}_i)$ね。ここからペアワイズATEが推定できる。
　いっぽうペアワイズATTは... [めんどくさいので略]

　ここからは、傾向スコアの推定方法。
　もっとも一般的なのは多項ロジスティック回帰を使う方法である。しかし、共変量の交互作用項とかをどこまで入れるかの判断が難しくて... [いろいろ書いてあるけどパス]
　そこでGBMを使おう。いろいろ比べたらGBMが一番良かったという話もあるぞ[McCaffrey, Ridgeway, & Morral (2004 Psych.Methods), Harder, Stuart, & Anthony (2010 Psych.Methods)というのが挙げられている。なお、この論文中には、GBMとはなんぞやという説明はほとんど出てこない。割り切っておるなあ]。

　まずは処理が2水準の場合について。
　GBMの反復をどこでストップするか。いくつかの基準がある。

　次に、処理が多水準でestimandがATEの場合。
　傾向スコア推定にあたってのお勧めの方法は、多項のモデルを組むのではなく、ある水準$t$に注目し、「対象者が$t$に属する確率」$\hat{p_t}(\mathbf{X}_i)$を求めるGBMを組む、というのを全水準について繰り返すこと。当然ながら、 $\hat{p_1}(\mathbf{X}_i) + \hat{p_2}(\mathbf{X}_i) + \cdots$は1にならない。でもそんなのどうでもいい。話のポイントは、各水準と全体との間で共変量をバランスさせることなのだ。[←へええええ！]
　反復の停止にあたっても「$t$ vs. 全体」での共変量バランスを監視する。標準化バイアスは
　$PSB_{tk} = | \bar{X}_{kt} - \bar{X}_{kp} | / \hat{\sigma}_{kp}$
$ \bar{X}_{kp}, \hat{\sigma}_{kp}$ は全群をプールして重み付けなしで算出する。KS統計量は
　$KS_{tk} = sup_x | EDF_{tk}(x) - EDF_{pk}(x) |$
$ EDF_{pk}(x)$は全群をプールして重み付けなしで算出する。
　なお、バランスの要約統計量を示す際には、PSB, KSの全群を通した最大値を使うとよい。

　処理が多水準で、estimandがATTの場合は... [いまあまり関心ないのでパス]

　ところで、doubly robust推定というのもあってだね... ウェイティングしても共変量のインバランスは少しは残るわけで、ウェイティングするだけでなく、さらに共変量を投入した重み付き回帰モデルを組むことがある。これを推奨する人もいるし、確かに処理効果の推定はより正確になるらしいんだけど、変数選択しなきゃいけないというのが決定。著者らのお勧めは、基本はウェイティングのみとし、どうしてもdoubly robust 推定したい場合は「まだインバランスが残っている共変量」を実質科学的な観点から選択すること。RCTでも設計段階で共変量を実質科学的に特定するし、事後的に調整するときにあらためて変数選択なんてしないでしょ、という理屈。

　最後に、有効サンプルサイズについて。ウェイティングで分散は拡大する。そのインパクトを捉える保守的な指標として、
　$\displaystyle ESS_t = \left( \sum_i T_i[t] w_i \right)^2 / \sum_i T_i[t] w_i^2$
を用いる。ここで$w_i$は、ATEなら$1/\hat{p}_t (\mathbf{X}_i)$ね。有効サンプルサイズが小さくなると云うことは、少数のケースにすごいウェイトがついているということ、つまり オーバーラップが十分でないというシグナルである。

　やれやれ、疲れた。以上が前半のメモ。
　後半は事例紹介。すごく役に立ちそうだが、必要になったときに慌てて読むってことにしよう。[←自分に甘い]

　処理の水準数が3以上のときの傾向スコア調整で、共変量から各水準への所属確率を推定するんだけど、その推定はなにも多項ロジスティック回帰のようなひとつのモデルでやらなくても、水準ごとに別々のモデルでよいし、ある対象者について確率の和が1にならなくても別にいいじゃん... というところが意外であった。そういうもんなんすか－。

論文：データ解析(2015-) - 読了：McCaffrey, et al. (2013) 処理の水準数が多いときの傾向スコア推定 by 一般化ブースト回帰

Bookcover 往生要集―日本浄土教の夜明け (1) (東洋文庫 (8)) [a]
源信 / 平凡社 / 1963-12-01

Bookcover 浄土真宗とは何か - 親鸞の教えとその系譜 (中公新書) [a]
小山 聡子 / 中央公論新社 / 2017-01-17

Bookcover 日本精神史: 自然宗教の逆襲 (単行本) [a]
利麿, 阿満 / 筑摩書房 / 2017-02-23

哲学・思想(2011-) - 読了：「往生要集 日本浄土教の夜明け」「浄土真宗とは何か 親鸞の教えとその系譜」「日本精神史 自然宗教の逆襲」

Bookcover 集合知入門 (I・O BOOKS) [a]
赤間 世紀 / 工学社 / 2014-05-01
2014年の本。どんなことが書いてあるのかなと思ってパラパラめくっただけなので、読了というのも失礼だが、整理の都合上記録しておく。
　様相論理の話が妙に充実していた。どういう読者のために書かれた本なんだろう？

データ解析 - 読了：「集合知入門」

Bookcover 夜の谷を行く [a]
夏生, 桐野 / 文藝春秋 / 2017-03-31

Bookcover ハイ・ライズ (創元SF文庫) [a]
J・G・バラード / 東京創元社 / 2016-07-10

Bookcover 罪悪 (創元推理文庫) [a]
フェルディナント・フォン・シーラッハ / 東京創元社 / 2016-02-12

Bookcover その雪と血を(ハヤカワ・ミステリ) (ハヤカワ・ミステリ 1912) [a]
ジョー・ネスボ / 早川書房 / 2016-10-06

フィクション - 読了：「夜の谷を行く」「ハイ・ライズ」「罪悪」「その雪と血を」

Bookcover 闇金ウシジマくん (39) (ビッグコミックス) [a]
真鍋 昌平 / 小学館 / 2017-04-28

Bookcover アイアムアヒーロー 22 (ビッグコミックス) [a]
花沢 健吾 / 小学館 / 2017-03-30

コミックス(2015-) - 読了：「闇金ウシジマくん」「アイアムアヒーロー」

Bookcover オリオリスープ(3) (モーニング KC) [a]
綿貫 芳子 / 講談社 / 2016-12-22

Bookcover ふつつかなヨメですが! (4) (ビッグコミックス) [a]
ねむ ようこ / 小学館 / 2017-01-12

Bookcover どこか遠くの話をしよう 上 (ビームコミックス) [a]
須藤 真澄 / KADOKAWA / 2017-03-25

Bookcover 娘の家出 6 (ヤングジャンプコミックス) [a]
志村 貴子 / 集英社 / 2017-04-19

Bookcover 僕らはみんな河合荘 9巻 (ヤングキングコミックス) [a]
宮原 るり / 少年画報社 / 2017-04-28

コミックス(2015-) - 読了：「オリオリスープ」「ふつつかなヨメですが！」「どこか遠くの話をしよう」「娘の家出」「僕らはみんな河合荘」

Bookcover 猫のお寺の知恩さん (3) (ビッグコミックス) [a]
オジロ マコト / 小学館 / 2017-02-28

Bookcover 木根さんの1人でキネマ 3 (ヤングアニマルコミックス) [a]
アサイ / 白泉社 / 2017-01-27

Bookcover BLUE GIANT (10) (ビッグコミックススペシャル) [a]
石塚 真一 / 小学館 / 2017-03-10

Bookcover BLUE GIANT SUPREME（１） (ビッグコミックススペシャル) [a]
石塚真一 / 小学館 / 2017-03-10

Bookcover 恋は雨上がりのように（７） (ビッグコミックス) [a]
眉月じゅん / 小学館 / 2017-03-10

コミックス(2015-) - 読了：「猫のお寺の知恩さん」「木根さんの1人でキネマ」「BLUE GIANT」「BLUE GIANT SUPREME」「恋は雨上がりのように」

Bookcover 甘々と稲妻(8) (アフタヌーンKC) [a]
雨隠 ギド / 講談社 / 2017-01-06

Bookcover 孤食ロボット 4 (ヤングジャンプコミックス) [a]
岩岡 ヒサエ / 集英社 / 2017-01-25

Bookcover 辺獄のシュヴェスタ (5) (ビッグコミックス) [a]
竹良 実 / 小学館 / 2017-02-10

Bookcover めしばな刑事タチバナ 24 (トクマコミックス) [a]
坂戸佐兵衛,旅井とり / 徳間書店 / 2017-01-31

Bookcover めしばな刑事タチバナ 25 (トクマコミックス) [a]
坂戸佐兵衛,旅井とり / 徳間書店 / 2017-03-31

Bookcover アルテ 6 (ゼノンコミックス) [a]
大久保圭 / 徳間書店 / 2017-01-20

コミックス(2015-) - 読了：「孤食ロボット」「辺境のシュヴェスタ」「めしばな刑事タチバナ」「甘々と稲妻」「アルテ」

Bookcover あれよ星屑 6 (ビームコミックス) [a]
山田 参助 / KADOKAWA / 2017-03-25

Bookcover 打ち切り漫画家(28歳)、パパになる。 (ヤングアニマルコミックス) [a]
富士屋カツヒト / 白泉社 / 2017-03-29

Bookcover ゲレクシス(2)<完> (イブニングKC) [a]
古谷 実 / 講談社 / 2017-03-23

Bookcover 重版出来! (9) (ビッグコミックス) [a]
松田 奈緒子 / 小学館 / 2017-04-12

Bookcover ダンジョン飯 4巻 (HARTA COMIX) [a]
九井 諒子 / KADOKAWA / 2017-02-15

コミックス(2015-) - 読了：「あれよ星屑」「打ち切り漫画家(28歳)、パパになる。」「ゲレクシス」「重版出来」「ダンジョン飯」

Bookcover 大人スキップ 1 (ビームコミックス) [a]
松田 洋子 / KADOKAWA / 2017-02-25

Bookcover 帰る場所 (ビームコミックス) [a]
近藤 ようこ / KADOKAWA / 2017-02-25

Bookcover ランド（４） (モーニングコミックス) [a]
山下和美 / 講談社 / 2017-01-23

Bookcover ヴィンランド・サガ（１９） (アフタヌーンコミックス) [a]
幸村誠 / 講談社 / 2017-04-21

Bookcover おもたせしました。1 (BUNCH COMICS) [a]
うめ(小沢高広・妹尾朝子) / 新潮社 / 2017-04-08

コミックス(2015-) - 読了：「大人スキップ」「帰る場所」「ランド」「ヴィンランド・サガ」「おもたせしました。」

Bookcover いぬやしき(8) (イブニングKC) [a]
奥 浩哉 / 講談社 / 2017-01-23

Bookcover ゴールデンゴールド（１） (モーニングコミックス) [a]
堀尾省太 / 講談社 / 2016-06-23

Bookcover ゴールデンゴールド(2) (モーニング KC) [a]
堀尾 省太 / 講談社 / 2017-01-23

Bookcover 春と盆暗 (アフタヌーンKC) [a]
熊倉 献 / 講談社 / 2017-01-23

Bookcover 伊豆漫玉日記 (ビームコミックス) [a]
桜 玉吉 / KADOKAWA / 2017-01-25

Bookcover めしにしましょう(1) (イブニングKC) [a]
小林 銅蟲 / 講談社 / 2016-11-22

コミックス(2015-) - 読了：「いぬやしき」「ゴールデンゴールド」「春と盆暗」「伊豆漫玉日記」「めしにしましょう」

Bookcover コトノバドライブ(4)<完> (アフタヌーンKC) [a]
芦奈野 ひとし / 講談社 / 2017-03-23

Bookcover 忘却のサチコ (6) (ビッグコミックス) [a]
阿部 潤 / 小学館 / 2016-05-30

Bookcover 幸せのマチ (Nemuki+コミックス) [a]
岩岡ヒサエ / 朝日新聞出版 / 2017-01-25

Bookcover 淋しいのはアンタだけじゃない (2) (ビッグコミックス) [a]
吉本 浩二 / 小学館 / 2017-02-28

Bookcover ワカコ酒 8 (ゼノンコミックス) [a]
新久千映 / 徳間書店 / 2017-01-20

コミックス(2015-) - 読了：「コトノバドライブ」「忘却のサチコ」「幸せのマチ」「寂しいのはアンタだけじゃない」「ワカコ酒」

Bookcover 大奥 14 (ヤングアニマルコミックス) [a]
よしながふみ / 白泉社 / 2017-02-28

Bookcover ディザインズ(2) (アフタヌーンKC) [a]
五十嵐 大介 / 講談社 / 2017-03-23

Bookcover 海街diary 8 恋と巡礼 (フラワーコミックス) [a]
吉田 秋生 / 小学館 / 2017-04-10

Bookcover 怒りのロードショー [a]
マクレーン / KADOKAWA / 2017-01-30

Bookcover レイリ(3)(少年チャンピオン・コミックス・エクストラ) [a]
岩明 均,室井 大資 / 秋田書店 / 2017-04-07

コミックス(2015-) - 読了：「大奥」「ディザインズ」「海街diary」「怒りのロードショー」「レイリ」

Bookcover 新戸ちゃんとお兄ちゃん（１） (ポラリスCOMICS) [a]
岡田ピコ / ほるぷ出版 / 2015-07-15

Bookcover たそがれたかこ(9) (KCデラックス) [a]
入江 喜和 / 講談社 / 2017-02-13

Bookcover 銃座のウルナ 3 (ビームコミックス) [a]
伊図透 / KADOKAWA / 2017-02-25

Bookcover 雑草たちよ 大志を抱け (フィールコミックスFCswing) [a]
池辺 葵 / 祥伝社 / 2017-02-08

Bookcover あさひなぐ (22) (ビッグコミックス) [a]
こざき 亜衣 / 小学館 / 2017-02-28

コミックス(2015-) - 読了：「新戸ちゃんとお兄ちゃん」「たそがれたかこ」「銃座のウルナ」「雑草たちよ大志を抱け」「あさひなぐ」

Bookcover 木曜日のフルット 6 (少年チャンピオン・コミックス) [a]
石黒正数 / 秋田書店 / 2017-03-08

Bookcover プリニウス5 (バンチコミックス45プレミアム) [a]
ヤマザキマリ,とり・みき / 新潮社 / 2017-02-09

Bookcover ペリリュー ─楽園のゲルニカ─ 1 (ヤングアニマルコミックス) [a]
武田一義,平塚柾緒(太平洋戦争研究会) / 白泉社 / 2016-07-29

Bookcover ペリリュー ─楽園のゲルニカ─ 2 (ヤングアニマルコミックス) [a]
武田一義,平塚柾緒(太平洋戦争研究会) / 白泉社 / 2017-01-27

Bookcover それでも町は廻っている 16巻 (ヤングキングコミックス) [a]
石黒 正数 / 少年画報社 / 2017-02-14

Bookcover 結んで放して (アクションコミックス) [a]
山名沢湖 / 双葉社 / 2016-11-28

コミックス(2015-) - 読了：「水曜日のフルット」「プリニウス」「ペリリュー」「それでも町は廻っている」「結んで放して」

Bookcover 三代目薬屋久兵衛 5 (Feelコミックス) [a]
ねむようこ / 祥伝社 / 2017-03-08

Bookcover おかあさんの扉6 ピッカピカです六歳児 (オレンジページムック) [a]
伊藤 理佐 / オレンジページ / 2017-02-02

Bookcover 続 数寄です! 2 (愛蔵版コミックス) [a]
山下 和美 / 集英社 / 2017-02-24

Bookcover アレンとドラン(1) (KC KISS) [a]
麻生 みこと / 講談社 / 2017-03-13

Bookcover 東京タラレバ娘(7) (KC KISS) [a]
東村 アキコ / 講談社 / 2017-01-13

Bookcover 東京タラレバ娘（８） (Ｋｉｓｓコミックス) [a]
東村アキコ / 講談社 / 2017-04-13

Bookcover 東京タラレバ娘(9)<完> (KC KISS) [a]
東村 アキコ / 講談社 / 2017-07-13

コミックス(2015-) - 読了：「三代目薬屋久兵衛」「おかあさんの扉」「続 数寄です!」「アレンとドラン」「東京タラレバ娘」

読んだ本が随分溜まってしまったので、遡って記録しておく。まずはコミックスから...

Bookcover 逃げるは恥だが役に立つ(9) (KC KISS) [a]
海野 つなみ / 講談社 / 2017-03-13

Bookcover うつヌケ うつトンネルを抜けた人たち [a]
田中 圭一 / KADOKAWA / 2017-01-19

Bookcover 田中圭一の「ペンと箸」: -漫画家の好物- (ビッグコミックススペシャル) [a]
田中 圭一 / 小学館 / 2017-01-12

Bookcover ダーリンは71歳 (コミックス単行本) [a]
理恵子, 西原 / 小学館 / 2017-01-19

Bookcover 大阪ハムレット(5) (アクションコミックス) [a]
森下 裕美 / 双葉社 / 2017-02-28

コミックス(2015-) - 読了：「逃げるは恥だが役に立つ」「うつヌケ うつトンネルを抜けた人たち」「田中圭一の「ペンと箸」漫画家の好物」「ダーリンは71歳」「大阪ハムレット」

2017年8月21日 (月)

Ridgeway, G., Kovalshik, S.A., Griffin, B.A., Kabeto, M.U. (2015) Propensity score analysis with survey weighted data. Journal of Causal Inference, 3(2), 237-249.
　仕事の都合で慌てて読んだ。調査設計のせいで標本ウェイトがついているデータについて傾向スコアを使った分析をするときどうすればいいか、という論文。楽しかないけど切実な話です。
　この雑誌、最近創刊された奴だが、たしかPearlさんが編集長かなにかなので、きっとパス図の話とか有向分離の話とかしか出てこないんだろうと思っておりました。傾向スコアの話も載るんすね。すいませんでした。
　
　適当に流し読みしただけなので、メモもいいかげんだけど...

　なにが問題になっておるのかというと、こういう話だ。
　2水準の処理で、ケース$i$の処理インジケータを$t_i$とし(処理群だったら$t_i = 1$)、potential outcomeを$y_{0i}, y_{1i}$とする。話を簡単にするために、PATT (処理群の平均処理効果の期待値)をestimandとする。で、残念ながら標本抽出の確率$p_i$が不均一であるとする。
　処理群の処理下アウトカムの期待値は単純に
　$\displaystyle E(y_1| t=1) \approx \frac{\sum_i t_i (1/p_i) y_{1i}}{\sum_i t_i (1/p_i)}$
でよい(いや抽出確率の不均一性はいわゆるモデルベースで解決しようという意見もあるだろうけど、それは脇に置いておき、デザインベースでなんとかする路線で考える)。
　問題は反事実下の期待値$E(y_0 | t=1)$の推定である。仮に統制群の傾向スコアを標本ウェイトなしで推定すると、統制群の共変量の分布を処理群の標本における分布とバランスさせることになってしまう。でもほんとにバランスさせないといけない相手は処理群の母集団における分布じゃないですか。というのが問題。

　フォーマルに書くと以下の通り。
　傾向スコアでウェイティングするとしよう。標本抽出インジケータを$s$ (抽出されたら1)、共変量ベクトルを$\mathbf{x}$として
　$f(\mathbf{x} | t=1) = w(\mathbf{x}) f(\mathbf{x} | t=0, s=0)$
となるウェイト$w(\mathbf{x})$が欲しい。
　これを書き換えると下式となる由：
　$\displaystyle w(\mathbf{x}) = \frac{f(s=1, t=0)}{f(t=1)} \frac{1}{f(s=1|t=0,\mathbf{x})}\frac{f(t=1|\mathbf{x})}{1-f(t=1|\mathbf{x})} $
　第1項は定数、第2項は標本ウェイト。問題は第3項で、これはよくみると母集団における処理割付オッズを表しており、標本における処理割付確率$f(t=1|\mathbf{x}, s=1)$から求めたオッズとは異なる、というのがポイント。

　というわけで、著者らいわく、「傾向スコアを求めるときには標本ウェイトは気にしなくてよい」という人も多いけど間違っとる。傾向スコアのモデルも標本ウェイトの下で組むべし。

　特にそれが必要な場面として、著者らは3つの場面を挙げている。(1)標本ウェイトを作った際の共変量$z$が傾向スコアを作る際には手に入らない場合。(2)傾向スコアモデルの自由度が小さいとき。(3)標本ウェイトを別のデータソースを使って出しているとき。
　シミュレーションと実例...[読んでない]。

　というわけで、諸君、傾向スコアのモデルを組む際にも標本抽出ウェイトを使いなさい。そして最終的なウェイトは傾向スコアのウェイトと標本抽出ウェイトの積にしなさい。云々。

　きちんと読んでないのでわかんないんだけど、うーん、逆にいうと、標本ウェイトが比較的に単純で(層別一段抽出とかで)、その算出にあたって使った層別変数が傾向スコアを求める際の共変量群にはいってて、標本サイズが十分であれば、傾向スコアモデルの構築の際には標本ウェイトは気にしなくてよい。という理解であっておりますでしょうか？？？

論文：データ解析(2015-) - 読了：Ridgeway, Kovalshik, Griffin, Kabeto (2015) それが標本ウェイトつきのデータなら、傾向スコアを求める際にも標本ウェイトを使え

Thoemmes, F.J., & Kim, E.S.(2011) A Systematic Review of Propensity Score Methods in the Social Science. Multivariate Behavioral Research, 46, 90-118.
　傾向スコア調整を使っている心理・教育系論文を集めてレビューし教訓を垂れます・イン・2011、という論文。わーい、心理・教育系だいすきー。だって数学が苦手な人が多いんだもんー。(すいません)

　まずイントロとして傾向スコア概説。いくつかメモしておくと、

　心理教育系で傾向スコアを使っている論文を111本集めてコーディングし集計。ちゃんと読んでないけど、えーっと、傾向スコアの推定方法は78%の論文がロジスティック回帰でやっている。共変量選択についてはちゃんと書いてないのが多い。傾向スコアの使い方はマッチングが64%(やり方はいろいろ)で、以下、層別、ウェイティング、共変量投入と続く。云々、云々。

　というわけで、諸君、以下の点を改善したまい。

　... 傾向スコアの使い方として時々みかけるdoubly robust推定って、あれどうなんすかね、なんか書いてあるといいな、と思いながらめくっていたのだが、残念ながら載ってなかった。

論文：データ解析(2015-) - 読了：Thoemmes & Kim (2011) 心理・教育系研究における傾向スコアの使われ方レビュー

　たまたま見つけた面白そうな論文。仕事が押している折りも折り、夕方のお茶菓子代わりに読んだ。なにやってんだか。
　キャッチーなタイトルもさることながら("The Heart Trumps the Head", もちろん米大統領の名と掛けている)、基礎心理学分野の最高峰誌にして重厚長大な論文が多いJEP:Generalに、こういうショート・リポートが載るのね、という驚きがある。

Tappin, B.M., van der Leer, L., McKay, R.T. (2017) The heart trumps the head: Desirability bias in political belief revision. Journal of Experimental Psychology: General. Advance online publication.

　いわく。
　信念に新情報を統合するやりかたについて２つの仮説がある。

このふたつの分離はふつう難しい。信念を確証する情報は望ましい情報でもあることが多いからだ。本研究では、政治的信念の更新という文脈で分離を試みます。舞台は2016年米大統領選。自分の支持とは別の問題として、きっとクリントンが勝つだろうと思っていた人が多かった。望ましさバイアスと確証バイアスが分離できる好例である。

　手法。
　事前登録研究です。対象者はAmazon Mechanical Turkで集めた米居住者900名。フィラー課題で一部除外し、結局811名を分析する。
　手順は以下の通り。

  1. スクリーニング質問：
    • a. 誰が勝つのが望ましいか：{トランプ、クリントン、どちらも望ましくない}
    • b. どちらが勝つと思うか：クリントン(0点)-トランプ(100点)の両極スライダーで回答
  2. aで「どちらも望ましくない」と答えた人、bでちょうど真ん中に回答した人は対象者から除外する。通過者は次の通り。＜望ましい候補者-勝つであろう候補者＞の順に、
    • ＜トランプ－トランプ＞127人
    • ＜クリントン－クリントン＞279人
    • ＜クリントン－トランプ＞91人
    • ＜トランプ－クリントン＞314人
    [おおっと... AMTでリクルートしたら、トランプ支持者のほうがやや多かったわけね...]
  3. フィラー課題。
  4. 証拠提示。全国世論調査の結果を読ませる。{クリントン有利, トランプ有利}の2条件。
  5. またフィラー課題。
  6. 本課題。上記b.を再聴取する。

　というわけで、2(望ましい候補者)x2(勝つであろう候補者)x2(証拠提示)の被験者間8セルができるわけだが、以下では候補者名は潰して2x2デザインとして捉える。つまり、(事前信念と証拠の{一致/不一致}) x (事前信念と望ましさの{一致/不一致})。
　設問b.(1回目, 2回目)の回答を、50点から事前信念方向へのずれとしてスコア化したのち、証拠方向への差を正として1回目と2回目の差をとり、これを信念更新スコアとする。[たとえば1回目の回答が80点, 提示された証拠は「クリントン有利」、2回目の回答が70点だったら、信念更新スコアは+10、ということであろう]

　結果。
　信念更新スコアの平均は以下の通り。

　1回目スコアを共変量にいれたANCOVAだと、望ましさの主効果は有意、確証の主効果もいちおう有意、交互作用も有意で、望ましさバイアスは確証時に高い。
　スコアの分布が歪んでいるので、それを考慮してあれこれ分析すると[すいませんちゃんと読んでません]、望ましさバイアスはロバストだが、確証バイアスはそうでもない由。
　政治的に右の人のほうが望ましさバイアスが強いんじゃないかという仮説があるが、そちらは支持できなかったとかなんとか。[ちゃんと読んでない]

　考察。
　望ましさバイアスはロバスト。確証バイアスは限定的。
　本研究からの示唆：

云々。
　
　なるほどねえ... 興味本位でめくったんだけど、仕事とも案外関係がある話であった。
　予測研究の文脈ではcitizen forecastという言葉があって、たとえば選挙予測で、あなたは誰に投票しますかと聞くより、あなたは誰が勝つと思いますかと聞いたほうが、集計結果の予測性能が良いという話がある。いっぽうこの研究はcitizen forecastにおける強い望ましさバイアスを示していることになる。
　citizen forecastに限らず、未来の事象について集合知による予測を試みる際には、予測対象について強い事前信念を持っている人を外すより、強い願望を持っている人を外したほうがいいのかもしれない。

論文：心理 - 読了：Tappin, et al.(2017) 確証バイアスと望ましさバイアス、どちらが深刻か？(あるいは：トランプ勝利を予測できなかったのは頭のせいかハートのせいか？)

2017年8月20日 (日)

Little, R.J.A., Wu, M.M. (1991) Models for contingency tables with known margins when target and sample population differ. Journal of the American Statistical Association. 86(413)
　仕事の都合で読んだ奴。

　ここにサーベイ調査から得たA, Bのクロス表がある。また、センサスから得たA, Bそれぞれの分布がある(クロス表は手に入らない)。サーベイ調査から得たクロス表の周辺分布は、センサスから得た分布と比べて少しずれている。
　以上に基づき、AとBの同時分布を推定したい。ただし、それはセンサスから得た分布と一致していないと困る。
　フォーマルに書くとこうだ。目標母集団において$A=i$かつ$B=j$である確率を$\pi_{ij}$とする。$\pi_{i+}, \pi_{+j}$を既知の周辺分布とする。サーベイ調査におけるセル割合を$p_{ij} = n_{ij}/n$とする。セル割合の推定量$\hat{\pi}_{ij}$が欲しいんだけど、$\sum_j \hat{\pi}_{ij} = \pi_{i+}, \sum_i \hat{\pi}_{ij} = \pi_{+j}$でないと困る。どうすればよいか。

　この問題はDeming&Stephan(1940)に遡り、たくさんの解が提案されておる。4つの解をご紹介しよう。

　その1, raking推定量(以下RAKEと略記)。デミングらの提案である。
　彼らの発想は、重みつき最小二乗
　$\sum_i \sum_j (p_{ij}-\hat{\pi}_{ij})^2 / p_{ij}$
を最小にしようというものであった。そこでデミングらが考えたのが、ご存じIPF(iterative proportional fitting)法、またの名をDeming-Stephanアルゴリズムである。なお、クロス表にIPFを掛けることをrakingということもあるので、ここではそう呼びます。
　これはどういうのかというと...[以下、表記を大幅に簡略化する]
　(1)$\hat{\pi}_{ij}=p_{ij}$とする。当然、周辺割合は既知の周辺分布と比べてずれている。(2)各セルに$\pi_{i+}/\hat{\pi}_{i+}$を掛け、行側の周辺割合を既知の周辺分布に無理やり合わせる。列側はずれたまま。(3)各セルに$\pi_{+j}/\hat{\pi}_{+j}$を掛け、列側の周辺割合を既知の周辺分布に無理やり合わせる。今度は行側がちょっぴりずれる。(4)気が済むまで繰り返す。
　のちにStephan(1942) 自身が指摘したんだけど、raking推定量は実は重みつき最小二乗推定量になっていない。なお、raking推定量は次の形式になっている：
　$\ln(\hat{\pi}_{ij} / p_{ij}) = \hat{\mu} + \hat{\alpha}_i + \hat{\beta}_j$

　その2、重みつき最小二乗推定量(LSQ)。Stephan(1942)が改めて提案したもの。これは
　$\hat{\pi}_{ij} / p_{ij} = \hat{\mu} + \hat{\alpha}_i + \hat{\beta}_j$
の形をとる[←へー。標本セル割合に対する倍率が、全体パラメータ, 列パラメータ, 行パラメータの和になるわけだ]。

　その3、無作為抽出下の最尤推定量(MLRS)。無作為抽出を仮定すれば、対数尤度は
　$l(\hat{\pi}) = \sum_i \sum_j p_{ij} \ln(\hat{\pi}_{ij})$
となるわけで、これを最大化する。この推定量は
　$(\hat{\pi}_{ij} / p_{ij})^{-1} = \hat{\mu} + \hat{\alpha}_i + \hat{\beta}_j$
という形式となる。

　その4、最小カイ二乗推定量(MCSQ)。
　$\sum_i \sum_j (\hat{\pi}_{ij} - p_{ij})^2 / \hat{\pi}_{ij}$
を最小化する。結局
　$(\hat{\pi}_{ij} / p_{ij})^{-2} = \hat{\mu} + \hat{\alpha}_i + \hat{\beta}_j$
という形式となる[←へえええ。そういうもんすか...]

　この4つの推定量は、無作為抽出の下では漸近的に等しいし、大した差はない。
　しかあし。この問題が生じるのは、往々にして、クロス表の元になったデータは無作為標本ですと胸を張って言えない状況においてある(だからこそ、既知の周辺分布に合わせたいなんて思うわけである)。
　目標母集団と抽出母集団が異なるとき、優れている推定量はどれだろうか？ これが本論文の本題であります。

　この話、目標母集団と抽出母集団がどう異なるのかによって話が変わってくる。
　目標母集団のセル割合を$\pi_{ij}$、抽出母集団のセル割合を$\tau_{ij}$としよう。いま、標本が抽出母集団からの単純無作為抽出であり、かつ
　$\ln(\pi_{ij}/\tau_{ij}) = \mu + \alpha_i+ \beta_j$
という関係があるならば(ただし$\sum a_i = \sum b_j = 0$)、RAKE推定量は$\{\pi_{ij}\}$の最尤推定量となる[←証明がついているんだけど読み飛ばした]。同様に、
　$\pi_{ij}/\tau_{ij} = \mu + \alpha_i+ \beta_j$
という関係があるならばLSQ推定量が、
　$(\pi_{ij}/\tau_{ij})^{-1} = \mu + \alpha_i+ \beta_j$
という関係があるならばMLRS推定量が、
　$(\pi_{ij}/\tau_{ij})^{-2} = \mu + \alpha_i+ \beta_j$
という関係があるならばMCSQ推定量が、$\{\pi_{ij}\}$の最尤推定量となるのである[←あー、なるほどねー！]。
　なお、ここから次の教訓が得られる。もし標本抽出においてAB交互作用があったら、どの推定量もうまくいかない。[←ああ、なるほど...これは直感的にもわかる気がする。いくらAとBの母周辺分布がわかっていても、標本抽出バイアスにAB交互作用があったら、それはお手上げだろうね]

　４つの推定量の分散はどうなっておるかというと... [パス]

　... 後半は事例とシミュレーション。このシミュレーションがこの論文の本題なんだけど、すいません、読み飛ばしました。いろんな標本抽出モデルで試した結果、RAKEとMLRSの成績が良かった由。
　著者ら曰く、確たる根拠があるわけじゃないけど、標本抽出モデルについての知識がない場合は、RAKE推定量がよさそうだ、とのことであった。

　なるほどねえ... とても勉強になりましたです。一見全然ちがう基準を持つ４つの推定方式が、実は統一的な枠組みで説明できるというところに痺れました。

　ほんというと... 同一母集団から得た2つの標本に、同一の選択肢を異なる状況下で選択させ、それぞれの状況での選択分布を得た。ここから、2つの状況を通じた同時分布(遷移行列というか混同行列というか)を推定したい。という問題に関心があるのである。仕事の話だから抽象的にしか書けないけど、そういう問題があるんです。
　この場合も、この論文のタイトルと同じくModels for contingency tables with known marginsが欲しいわけなんだけど、この論文で言うところのABクロス表(rakingの文脈で言うところのseed)は観察できないわけで、なんらかの事前知識からseedを構成することになる。たとえば、状況が選択に与える影響を最小限に評価したい、よってseedは対角行列だ、とか。
　この論文で取り上げられている４つの推定量はそれぞれの発想でなにかを最小化しているわけだけど、結果的には、セル割合の推定値とseedとの比をなんらか変換した $(\pi_{ij}/\tau_{ij})^{\lambda} $が全効果・行効果・列効果の線形和となるという制約をかけていることになるわけだ。これはこの論文から得た大きな学びでございました。私が考える問題では、seedの側に実質的な想定を置くかわり、seedと推定値とのずれについてはなにも想定したくないんだけど...? ううむ...

論文：データ解析(2015-) - 読了：Little & Wu (1991) 標本から得たAxBクロス表を既知の周辺分布に合わせたい、標本にはバイアスがあることがわかっている、さあどうするか

2017年8月19日 (土)

　Rのdplyrパッケージを使っていて困ることのひとつに、非標準評価(NSE)をめぐるトラブルがある。dplyrの関数のなかでは変数名を裸で指定できることが多い。これはとても便利なんだけど、ときにはかえって困ることもある。以前はいろんな関数に非標準評価版と標準評価版が用意されていたんだけど、最近は方針が変わったようだ。
　これはきっと深い話なんだろうけど、きちんと調べている時間がない。かといって、いざ困ったときにあわてて調べているようでは追いつかない。しょうがないので、dplyrのvignettesのひとつ"Programming with dplyr"を通読してメモを取っておくことにする。Rの達人からみればつまらない情報だと思うが、すいません、純粋に自分用の覚え書きです。

●.data代名詞。たとえば...

mutate_y <- function(df){

  mutate(df, y= .data$a + .data$b)

}

mutate_y(df1)

上の例ではa, bがdfの変数であることを明示している。仮に.dataをつけないと、dfの変数の中にa,bがないとき、グローバル環境にあるa,bが読まれちゃうかもしれない。
[←そうそう、そういうトラブルが時々ある。しょうがないから私は、危なそうなときはdplyrを呼ばず df$y <- df[,"a"] + df[,"b"] という風にクラシカルに書くか、関数の冒頭で stopifnot(c("a", "b") %in% colnames(df)) とトラップしていた。そうか.dataって書けばいいのか]

●quo()。たとえば、次のコードは通らない。

df <- tibble(

    g1 = c(1,1,2,2,2), 

    a = sample(5)

)

my_summarize <- function(df, group_var){

  df %>%

    group_by(group_var) %>%

    summarize(a = mean(a))

}

# my_summarize(df, g1)  はだめ

# my_summarize(df, "g1")  もだめ

そこで、関数にquosureを渡す。quo()は入力を評価せずクオートし、quosureと呼ばれるオブジェクトを返す。!!は入力をアンクオートする。UQ()と書いてもよい。

my_summarize <- function(df, group_var){

  df %>%

    group_by(!!group_var) %>%

    summarize(a = mean(a))

}

my_summarize(df, quo(g1))

●enquo()。上の例で、関数に裸の変数名を渡したいとしよう。enquo()は謎の黒魔術を用い(ほんとにそう書いてある)、ユーザが関数に与えた引数そのもの(ここではg1という変数名)をクオートしてくれる。

my_summarize <- function(df, group_by){

  group_by <- enquo(group_by)

  df %>%

    group_by(!!group_var) %>% 

    summarize(a = mean(a))

}

my_summarize(df, g1)

●quo_name()。たとえば

mutate(df, mean_a = mean(a), sum_a = sum(a))

mutate(df, mean_b = mean(b), sum_b = sum(b))

というようなのを関数にしたい。つまり、mean_a, sum_aといった新しい変数名を生成したいわけだ。こういうときはquo_name()でquosureを文字列に変換する。mutate()のなかの式の左辺で!!を使った時は、=ではなく:=を使う。

mu_mutate <- function(df, expr){

  expr <- enquo(expr)

  mean_name <- paste0("mean_", quo_name(expr))

  mutate(df, !!mean_name := mean(!!expr)

}

my_mutate(df, a)

●enquos()。下の例では複数の裸の変数名を渡している。enquos()は...をquosureのリストにして返す。!!!はquosureのリストをアンクオートしてつないでくれる(これをunquote-splicingという)。UQS()と書いても良い。

my_summarize <- function(df, ...){

  group_var <- enquos(...)

  df %>%

    group_by(!!!group_var ) %>%

    summarize(a = mean(a))

}

my_summarize(df, g1, g2)

　こうして書いてみると一見ややこしいけど、SASマクロ言語のクオテーションと比べれば全然わかりやすい。ああ、懐かしい...あれはほんとに、ほんとにわけがわからなかった...

　ところで、vignetteにいわく、疑似クオテーション(quasiquotation)という概念は哲学者W.V.O.クワインの40年代の著述に由来するのだそうだ。へえええ？

2020/01/22 ちょっぴり追記。

雑記：データ解析 - Rのdplyrパッケージでプログラミングするときの注意点

　先日リリースされたMplus 8では、時系列モデルの機能が大幅拡充されている。ただでさえ目も眩むほどに多機能なのに、MODELセクションにラグつき回帰を表す記号なんかが追加されて、もうえらいことになっている。勘弁してください、Muthen導師...

　Asparouhov, T., Hamaker, E.L., Muthen, B. (2017) Dynamic Structural Equation Models. Mplus technical paper.
　新機能についてのテクニカル・ペーパー。実戦投入前の儀式として読んだ。

　新機能が想定しているのは、たくさんの人をたくさんの時点で測定しました、というようなintensiveな縦断データ(ILDデータ)。ambulatory assessmentsとか[なんて訳すんだろう。移動測定？]、日記データとか、ecological memontary assesmenentデータとか[これも定訳があるのかどうかわかんないけど、患者の電子日記みたいなのだと思う]、経験サンプリングとか、そういうのである。

　いわく...
　社会科学における縦断分析の手法として成長モデリングが挙げられる。観察変数なり潜在変数なりを時間の関数としてモデル化し、そのパラメータを個人レベルのランダム効果とみなすわけである。でも一人当たり時点数はふつう10以下。データが大きいと計算が無理になるし、時点数が大きいと単純な関数を当てはめるのは難しくなる(スプラインをつかってもいいけど補外が難しい)。
　そこで動的構造方程式モデル(DSEM)を提案しよう。個人をクラスタとする2レベルモデルとして成長モデルを組み、そこにラグつきの回帰とかをいれる。Molenaar(1985)とかの動的構造モデルを2レベル化するといってもよい。[なるほど...さすがはMuthen導師、簡潔にして要を得た説明だ。しかし導師よ、Molenaar(1985)って引用文献に載ってないんですけど。Psychometrikaの動的因子分析の論文ですかね]

　わがDSEMフレームワーク、それは次の４つのモデリング技術の結合である。

  1. マルチレベル・モデリング。すなわち、個人ごとの効果がもたらす相関に基づくモデリング。
  2. 時系列モデリング。すなわち、観察の近接性がもたらす相関に基づくモデリング。
  3. 構造方程式モデリング。すなわち、変数間の相関に基づくモデリング。
  4. そして時変効果モデリング(EVEM)。すなわち、進化のステージが同じであることがもたらす相関に基づくモデリング。

[...か、かっこいい...導師...濡れちゃいます...(雨で)]

　能書きはこのくらいにして、モデルの話。
　まずはクロス分類モデル(個人のランダム効果と時点のランダム効果を併せたモデル)から。個人$i$、時点$t (=1,2,\ldots,T_i)$ における観察ベクトルを$Y_{it}$とする。これを分解する：
　$Y_{it} = Y_{1,it} + Y_{2,i} + Y_{3,t}$
順に、個人$i$時点$t$からの偏差, 個人の寄与, 時点の寄与。

　第2項, 第3項のモデルがbetweenレベルのモデルとなる。まず第2項は
　$Y_{2,i} = \nu_2 + \Lambda_2 \eta_{2,i} + K_2 X_{2,i} + \epsilon_{2,i}$
　$\eta_{2,i} = \alpha_2 + B_2 \eta_{2,i} + \Gamma_2 X_{2,i} + \xi_{2,i}$
上が測定方程式で下が構造方程式。$X_{2,i}$は個人レベルの時間不変な共変量、$\eta_{2,i}$は個人レベルの時間不変な潜在変数、$\epsilon_{2,i}$と$\xi_{2,i}$は平均ゼロの残差である。同様に第3項は
　$Y_{3,i} = \nu_3 + \Lambda_3 \eta_{3,i} + K_3 X_{3,i} + \epsilon_{3,i}$
　$\eta_{3,i} = \alpha_3 + B_2 \eta_{3,i} + \Gamma_3 X_{3,i} + \xi_{3,i}$

　さて、第1項のモデル、すなわちwithinレベルのモデル。いよいよ時系列が入ります。
　測定方程式は
　$Y_{1,it}$
　$= \nu_1$
　$+ \sum_{l=0}^L \Lambda_{1,l} \eta_{1,i,t-l}$
　$+ \sum_{l=0}^L R_l Y_{1,i,t-l}$
　$+ \sum_{l=0}^L K_{1,l} X_{1,i,t-l}$
　$+ \epsilon_{1,it}$
　構造方程式は
　$\eta_{1,it}$
　$= \alpha_1$
　$+ \sum_{l=0}^L B_{1,l} \eta_{1,i,t-l}$
　$+ \sum_{l=0}^L Q_l Y_{1,i,t-l}$
　$+ \sum_{l=0}^L \Lambda_{1,l} X_{1,i,t-l}$
　$+ \xi_{1,it}$
派手になってまいりました。順に、切片、潜在変数、観察従属変数、共変量、残差である。例によって、$X_{1,i,t}$は個人x時点の共変量、$\eta_{1,it}$は個人x時点の潜在変数。
　この定式化だと、withinレベルのモデルにおけるパラメータはランダム項ではないが、ランダム項にしてもいい。つまり、たとえば$\Lambda_{1,l}$を$ \Lambda_{1,lit}$としてもいいし、$R_l$を$R_{lit}$としてもよい。この場合、withinレベルのパラメータもまた個人と時点に分解する。つまり、いまパラメータ$s$をランダムにしたい場合は
　$s = s_{2,i} + s_{3,t}$
と考えるわけである。
　同様に残差分散$Var(\epsilon_{1,it}), Var( \xi_{1,it})$もランダムにしてよくて...[めんどくさいので略]

　以上の定式化は、時系列的特徴は自己相関しか取り入れていないように見えるけど、潜在変数があるので意外に柔軟である。たとえばARMA(1,1)は
　$Y_t = \mu + a Y_{t-1} + \eta_t + b\eta_{t-1}$
としてして表現できる。
　上のモデルだと、時点0以前のデータが必要になるけど、そこはその、MCMCのburninのあいだに適当な事前分布を決めてですね... [とかなんとか。なんだかわからんが、とにかくどうにかなる由]
　[他にもいくつか注意書きがあったけど、省略]

　推定に当たっては、モデルをブロックにわけて... [省略]

　モデルの適合度としてはDICを使う。すべての従属変数が連続だとする。モデルのパラメータを$\theta$, すべての観察変数を$Y$として、デビアンスは
　$D(\theta) = -2 \log p(Y|\theta)$
MCMCを通じて得たデビアンスの平均を$\bar{D}$, MCMCを通じて得たモデルパラメータの平均を$\bar{\theta}$とする。有効パラメータ数を次のように定義する：
　$p_D = \bar{D} - D(\bar{\theta})$
で、DICとは
　$DIC = p_D + \bar{D}$
DSEMモデルにおけるDICを厳密に定義すると... [略]。
　なお、DICにはいろいろ注意すべき点がある。

　モデルの評価のためには、標本統計量とモデルによるその推定量を比べるという手もある。たとえば、2レベルDSEMで従属変数がひとつ($Y$)のとき、個人$i$における$Y$の標本平均を標本統計量を$\bar{Y}_{i*} = \sum ^{T_i} _t Y_{it} / T_{i}$、そのモデルによる推定量を$\mu_i$として、$R = Cor(\mu_i, \bar{Y}_{i*})$ とか$MSE = \sum_i^{N} (\mu_i - \bar{Y}_{i*})^2 / N$とかを調べたりする。

　... 以上、前半のメモ。
　後半はシミュレーションの紹介。扱われている問題は以下の通り。

　長いので、関心のある部分だけつまみ食い。

　センタリングについて。
　次の単変量AR(1)モデルを考える。
　$Y_{it} = \mu_i + \phi_i (Y_{i,t-1} - \mu_i) + \xi_{it}$
$\xi_{it}$は平均0のホワイトノイズ、$\mu_i$と$\phi_i$は二変量正規とする。
　DSEMならこれを一発推定できるけど、普通の2レベル回帰だと、標本平均で中心化して
　$Y_{it} = \mu_i + \phi_i (Y_{i,t-1} - \bar{Y}_{i*}) + \xi_{it}$
を推定することになるわね。すると$\phi_i$にバイアスがかかる。これを動的パネルバイアス、ないしNickellのバイアスと呼ぶ。 Nickellさんの近似式によればバイアスは$-(1+\phi)/(T-1)$である。 [←へぇー]
　そこでシミュレーションしてみると... DSEMで一発推定した場合、バイアスは小さく、時系列が100時点以上ならほぼゼロ。標本平均で中心化した場合、Nickellの近似式はほぼ当たっている。云々...[後略]

　ARMA(1,1)とMEAR(1)について。
　ARMA(1,1)モデルとは
　$Y_t = \mu + \phi Y_{t-1} + \epsilon_t + \theta \epsilon_{t-1}$
だけど、これは次のモデルと等価である。
　$Y_t = \mu + f_t + \xi_t$
　$f_t = \phi f_{t-1} + e_t$
つまり、潜在変数$f_t$がAR(1)に従っているんだけど、その測定に誤差が乗っていると考えるわけである。これをmeasurement error AR(1)モデル、略してMEAR(1)と呼ぶことにする。云々... [あー、この話面白そう。時間がなくて読み飛ばしたけど、いつかきちんと勉強したい]

　動的因子分析(DFA)について。
　一般的なDFAモデルとして、直接自己回帰因子得点モデル(DAFS)とホワイトノイズ因子得点モデル(WNFS)がある。DAFSっていうのは
　$Y_t = \nu + \Lambda \eta_t + \epsilon_t$
　$\eta_t = \sum^L_{l=1} B_l \eta_{t-l} + \xi_t$
というモデルで、観察変数と潜在変数の間にはラグがなく、潜在変数がAR過程に従う。観察変数は結局ARMA(p,p)に従う(pは観察変数の数)。いっぽうWNFSってのは
　$Y_t = \nu + \sum^L_{l=0} \Lambda_l \eta_{t-l} + \epsilon_t$
というモデルで、観察変数と潜在変数の間にラグがあり、潜在変数はホワイトノイズ。観察変数は結局MA(L)に従う。
　これをハイブリッドにしたモデルを考えることもできる。すなわち
　$Y_t = \nu + \sum^L_{l=0} \Lambda_l \eta_{t-l} + \epsilon_t$
　$\eta_t = \sum^L_{l=1} B_l \eta_{t-l} + \xi_t$
　1因子5指標、$L=1$、100人100時点でシミュレーションしてみると、[...中略...]、ちゃんとDICで正しいモデルを選択できました。云々。[途中で疲れてきて読み飛ばしたが、この節、必要になったらきちんと読もう]

　...そんなこんなで、後半はほとんど読めてないんだけど、まあいいや。このtech. paperのmplusのコードは公開されているはずなので、いずれ余力ができたら勉強する、ということで。もっとも、どうせ余力なんて永遠に手に入らないのだが。

論文：データ解析(2015-) - 読了：Asparouhov, Hamaker, & Muthen (2017) ものども跪け、これがMplus8の新機能「動的SEM」だ

Asparouhov, T., Hamaker, E.L., Muthen, B. (2017) Dynamic latent class analysis. Structural Equation Modeling. 24, 257-269.

　哀れなデータ解析ユーザの諸君、Mplusがこのたび実装した時系列データ分析の世界へとご招待しよう。その名も動的潜在クラス・モデルだ。という論文。正直、そんなややこしい世界にはご招待してほしくないんですが。できればずっと寝ていたいんですが。

　いわく。
　[前置きをはしょって...]
　このモデリングの枠組みを提出する目的は：(a)異なる状態 (いわゆる潜在クラス、レジーム)のあいだでのスイッチングを説明する潜在マルコフモデル(隠れマルコフモデル)をつくりたい。(b)個人の遷移確率をランダム効果としてモデル化したい。(c)時系列分析とそのマルチレベルへの拡張を通じて、状態のあいだの動的な関係性を調べたい。
　すでに以上のうち２つの組み合わせは存在する。レジーム・スイッチング状態空間モデルとか、個人の遷移確率がランダムな隠れマルコフモデルとか。でも３つの組み合わせははじめて。
　[そのほか、まだまだイントロが続くけど、はしょって...]

　まずはMplusが実装しているDSEMフレームワークについて説明しよう。詳細はAsparouhov et al. (2016, Mplus Tech. Rep.) を参照のこと。
　個人$i$の時点$t$における観察ベクトルを$Y_{it}$とする。これをwithinレベルとbetweenレベルに分割して
　$Y_{it} = Y_{1,it} + Y_{2, i}$
いずれも正規分布に従う確率ベクトルとみなす。
　betweenレベルのほうは次のようにモデル化する。
　$Y_{2,i} = v_2 + \Lambda_2 \ \eta_{2,i} + \epsilon_{2,i}$
　$\eta_{2,i} = \alpha_2 + B_2 \ \eta_{2,i} + \Gamma_2 x_{2,i} + \xi_{2,i}$
　withinレベルのほうにはラグがはいって、
　$Y_{1,it} = \sum_{l=0}^L \Lambda_{1,i,l} \ \eta_{1,i,t-l} + \epsilon_{1,it}$
　$\eta_{1,i,t} = \alpha_{1,i} + \sum_{l=0}^{L} B_{1,i,l} \ \eta_{1,i,t-l} + \Gamma_{1,i} x_{1,it} + \xi_{1,it}$
[以下、Asparouhov et al. (2016) の簡略版的説明。省略]

　これを混合モデルへと拡張します。
　withinレベルの潜在クラス$S_{it}$を導入する。記号を$C$じゃなくて$S$にしたのは、時系列の文脈では「潜在状態変数」と呼ばれることが多いから。
　$[Y_{1,it}|S_{it} = s] = v_{1,s} + \sum_{l=0}^L \Lambda_{1,l,s} \ \eta_{i,t-l} + \epsilon_{it} $
　$[\eta_{i,t} |S_{it} = s] = \alpha_{1,s} + \sum_{l=0}^{L} B_{1,l,s} \ \eta_{i,t-l} + \Gamma_{1,s} x_{it} + \xi_{it}$
[記法の変化に注意。DSEMとのちがいをメモしておくと、(1)観察方程式にクラス別切片$v_{1,s}$が追加され、状態方程式の切片が個人別からクラス別になった。(2)観察方程式・状態方程式の係数が、個人別係数$\Lambda_{1,i,l}, B_{1,i,l}$からクラス別係数$\Lambda_{1,l,s}, B_{1,l,s}$に変わった。添え字の順序が変わった理由はよくわからない。(3)潜在変数、観察誤差、共変量、状態誤差の添え字から$1$がとれ、たとえば$\eta_{1,i,t}$から$\eta_{i,t}$になった。理由はわからない]
　$S_{it}$の分布は
　$\displaystyle P(S_{it} = s) = \frac{\exp(\alpha_{is})}{\sum_{s=1}^K \exp(\alpha_{is}) }$
ただし、$\alpha_{is}$は正規ランダム効果で、識別の都合上$\alpha_{iK}=0$とする。これは$\eta_{2,i}$の一部として含まれている。[←頭のなかが疑問符でいっぱいになったが、この$\alpha_{is}$は、betweenレベルの構造方程式の切片$\alpha_2$でもwithinレベルの構造方程式の切片$\alpha_{1,s}$でもなく、ここで初出の確率変数らしい。時間の添え字がついていないのは誤植かと疑ったが、どうやらこれで正しい模様。下記参照]
　[以下、 $\alpha_{is}$ の推定の話がしばらく続く。よくわからんので省略]

　以上のモデルには欠点がある。クラスのなかでは自己回帰をモデル化できてるけれども、潜在クラスの自己相関をモデル化できていない。つまり、上の$P(S_{it}=s)$のモデルをみるとわかるように、隣り合う二つの時点のあいだで個人が属するクラスが、$a_{is}$のもとで条件つき独立になっている[←そう！そうですよね！ だから$\alpha_{is}$が時間不変なのっておかしいと思ったのだ]。これはちょっと現実的でないので、あとで隠れマルコフモデル(HMM)を導入して手直しする。

　さて、ここでちょっと話かわって、マルチレベル混合モデルの事例紹介。いずれもランダム効果の数が多くて、理論的にはML推定できるけど、計算量的にはMCMCでないと歯が立たないものばかりである。

　事例1, データがクラスタ化されていて測定変動性がある潜在クラス分析。
　[従来のロバストML推定をディスるくだりがあって... ベイジアン化する前からのMplusユーザとしては、自分がディスられているようでちょっとつらい...]
　例として、3クラス, 2値項目8個のモデルを考える。クラスタ$j$の個人$i$の項目$p$の得点$U_{pij}$について
　$P(U_{pij} = 1 | C_{ij} = k) = \Phi(\tau_{pk} + \epsilon_{pj})$
とする。$\tau_{pk}$は閾値, $\epsilon_{pj}$はクラスタ間の測定変動ね。
　で、クラス所属確率を
　$\displaystyle P(C_{ij} = k) = \frac{\exp(\alpha_k + \alpha_{jk})}{\sum_{j=1}^K \exp(\alpha_k + \alpha_{jk}) }$
とする。識別のため、$\alpha_K, \alpha_{jK}$は0とする。
　このモデル、ML推定だと、 $\epsilon_{pj}$が8項目, $ \alpha_{jk}$が2クラス、計10次元の数値積分が必要になる。でもベイジアンならあっという間さ。

　事例2. 制約のない2レベル混合モデル。[パス]
　事例3. クラスタ別の遷移確率を持つマルチレベル潜在遷移分析。[これもパス。本題に入るまで体力を温存したい]

　隠れマルコフモデル(HMM)を導入します。
　HMMは測定モデルとマルコフ・スイッチング・モデルからなる。測定モデルは普通の混合モデルと同じで、$P(Y_t | C_t)$のモデル。マルコフ・スイッチング・モデルは遷移行列$P(C_t | C_{t-1})$のモデル。１レベルモデルなら、この遷移行列自体をパラメータとみてモデル化できる(自然共役事前分布としてディリクレ分布が使える)。周辺確率$P(C_t)$はパラメータでないことに注意。
　見方を変えると、HMMというのは１次自己回帰モデルである。云々...
　[以下、パラメータ推定方法の話とシミュレーションが続く。パス]

　お待たせしました。動的潜在クラスモデル(DLCA)の登場です。
　DLCAとは、ここまでに紹介した３つのアプローチの統合だ。(1)マルチレベルとSEMをあわせてマルチレベルSEM、さらに混合モデルをあわせてマルチレベル混合モデル、これに潜在遷移モデルをあわせてマルチレベル潜在遷移モデル。(2)時系列をSEMをあわせてDSEM、これに混合モデルをあわせて混合DSEMモデル。(3)HMM。
　まずは
　$Y_{it} = Y_{1,it} + Y_{2, i}$
withinレベルのほうがクラスごとのDSEMモデルとなり
　$[Y_{1,it} | S_{it} = s] = v_{1,s} + \sum_{l=0}^L \Lambda_{1,l,s} \ \eta_{i,t-l} + \epsilon_{it}$
　$[\eta_{i,t} | S_{ot} = s] = \alpha_{1,i} + \sum_{l=0}^{L} B_{1,l,s} \ \eta_{i,t-l} + \Gamma_{1,s} x_{it} + \xi_{it}$
潜在クラス$S_{it}$はマルコフ・スイッチング・モデル。
　$\displaystyle P(S_{it} = d | S_{i,t-1} = c) = \frac{\exp(\alpha_{idc})}{\sum_{k=1}^K \exp(\alpha_{ikc})}$
betweenレベルは
　$Y_{2,i} = v_2 + \Lambda_2 \eta_{2,i} + \epsilon_{2,i}$
　$\eta_{2,i} = \alpha_2 + B_2 \eta_{2,i} + \Gamma_2 x_{2,i} + \xi_{2,i}$

　事例1. 2クラスDLCA。[パス]
　事例2. マルチレベル・マルコフ・スイッチング自己回帰モデル。[パス]
　事例3. 潜在因子のレジーム・スイッチング。[パス]

　Mplusではもっともっと柔軟なモデルが組めるので使うがよろしい。
　さらなる課題：モデルの比較をどうするか。非定常時系列モデルをどうやって実現するか(共変量をいれる；時変効果をいれる)。時変する潜在クラスと時変しない潜在クラスの両方を入れる。などなど。

　... いやあ、眠かった。ふらふらになりながら読了。事例をほぼ全部スキップしてしまったが、必要になったらコードと一緒に勉強する、ということで。

論文：データ解析(2015-) - 読了：Asparouhov, Hamaker, & Muthen (2017) ものどもひれ伏せよ、これが動的潜在クラス分析だ

2017年8月18日 (金)

Scott, S.L., Varian, H. (2014) Predicting the Present with Bayesian Structural Time Series. International Journal of Mathematical Modelling and Numerical Optimisation, 5, 4-23.
　Googleの中の人謹製、ベイジアン構造時系列モデリングのためのRパッケージbstsの元論文。draftのPDFで読んだ。 別に読みたかないけど、実戦投入前の儀式としてぱらぱらめくった次第。

　このモデルでの主な使い道として想定されているのは、Google Trendsのようなたくさんの、そんなに長くない時系列があり、それらを予測子としてある目的変数の時系列をnowcastingしたいんだけど、でも予測子のうちほんとに効く奴はいくつかしかない、という状況である。動的因子分析なんかで多変量時系列を縮約するのではなく、ベイジアンモデル平均のアプローチで事後分布をシミュレートする。

　モデルの説明。
　時点$t$における観察値$y_t$について、次の状態空間表現を考える。
　観察方程式 $y_t = Z^T_t \alpha_t + e_t \ \ e_t \sim M(0, H_t)$
　遷移方程式 $\alpha_t = T_t \alpha_t + R_t \eta_t \ \ \eta_t \sim N(0, Q_t)$
さて、

　外的な予測子の効果$\beta^T \mathbf{x}$について。$\beta$は時変なしとし、$\alpha_t$に値1の変数を追加し、 $\beta^T \mathbf{x}$を$Z_t$に入れ込む。事前分布としてspike-and-slab事前分布を使う[メモは後述]。するとパラメータの事後分布がこんな風になる...[略]。推定にはMCMCをこんな風に使う...[略]。

　事例はふたつ。(1)週次の失業保険新規申請件数をGoogle Trendsで予測する。(2)月次の全米小売売上金額をGoogle Trendsで予測する。
　この方法で擬似相関が回避できるわけではないんだけど(実際、後者の例では変なキーワードの検索量時系列が売上金額の強力な予測子となっている)、分析者の主観的判断を事前分布として生かせるという点が特徴。

　... bstsパッケージというのはMARSSパッケージのMCMC版みたいなものかと思ってたんだけど、蓋をあけてみたらベイジアンモデル平均の話であった。なんでも読んでみるもんね。
　マニュアルをちらっとみたところでは、dlmパッケージのように要素別ヘルパー関数を組み合わせて使うようで、なんだか面白そうだ。と、自分で自分に景気をつけて...

　以下、spike-and-slab事前分布についてのメモ。ついつい逐語訳になってしまった。

　ベイジアン・パラダイムで[たくさん予測子があるけど効くのはわずかという]スパース性を表現する自然な方法として、回帰係数にspike and slab事前分布を与えるという方法がある。
　$\gamma_k$を、$\beta_k \neq 0$のときに$1$, $\beta_k=0$のときに$0$となる変数とする。$\beta$の非ゼロ要素からなる下位集合を$\beta_\gamma$とする。
　spike-and-slab事前分布とは
　$p(\beta, \gamma, \sigma^2_e = p(\beta_\gamma|\gamma, \sigma^2_e) p(\sigma^2_e |\gamma) p(\gamma)$

　$p(\gamma)$の周辺分布は「スパイク」である。つまり、それはゼロの位置に正の確率質量を持つ。原理的には、$p(\gamma)$を調整して階層原理のようなベスト・プラクティスを実現できる(階層原理とは、高次の交互作用項が入るときは低次の項も入るという原理)。実際には、単に独立ベルヌーイ事前分布を使うのが便利である [各予測子が独立に確率$\pi_k$でモデルに入るってことね] 。
　$\gamma \sim \sum_{k=1} \pi^{\gamma_k}_k (1-\pi_k)^{1-\gamma_k}$
もっと単純化して、すべての$\pi_k$を$\pi$とすることも多い。これは$\pi_k$をいちいちセットするのは大変だという主旨なのだけど、事前分布の交換可能性という基盤があれば正当化できる。$\pi$を決める自然な方法のひとつとして、分析者に「モデルの 期待されるサイズ」を尋ねるという手がある。分析者が「非ゼロの予測子は$p$個」というならば、$\mathbf{x_t}$の次元数を$K$として$\pi = p / K$とすればよい。場合によっては、特定の予測子について$\pi_k$を0か1に決め打ちするのも便利である。(我々は採用しないけど)別の戦略として、予測子を「モデルに入りそうか」でいくつかのグループに主観的に分け、それぞれのグループの予測子に主観的に決めた確率を与えるという手もある。

　正方行列$\Omega^{-1}$について、その行と列が$\gamma_k=1$に対応している行列を$\Omega^{-1}_\gamma$とする[←えええ...? 先生すいません、頭悪くてよくわかんないっす...]。条件つき事前分布$p(1/\sigma^2_e | \gamma)$と$p(\beta_\gamma | \sigma_e, \gamma)$は次の条件つき共役対として表現できる。
　$\beta_\gamma | \sigma^2_e, \gamma \sim N(b_\gamma, \sigma^2_e (\Omega^{-1}_\gamma)^{-1})$
　$\frac{1}{\sigma^2_e} | \gamma \sim Ga(\frac{\nu}{2}, \frac{ss}{2})$
ここで$Ga(r,s)$は平均$r/s$, 分散$r/s^2$のガンマ分布である。これが「スラブ」[厚板]である。なぜそう呼ぶかというと、すごく弱い情報性しか持たないように(一様に近づくように)パラメータを選べるからである。$\gamma$と同様、ここでも合理的なデフォルト値が存在する。まず、事前平均ベクトル$b$はゼロにするのが一般的である。ただし、特定の予測子が特に有用だという信念がある場合には、情報的な事前分布を指定することも容易である。$ss$と$\nu$は事前の平方和と事前のサンプルサイズだと解釈できる。これらはユーザに、回帰に期待する$R^2$と、その推測がどのくらいのサイズの観察と同じ重みをもつと思うか($\nu$)を尋ねてセットすればよい。ここで$ss/\nu = (1-R^2) s^2_y$である。$s^2_y$とは反応の周辺SDである。$s^2_y$でスケーリングするのはベイジアンのパラダイムからちょっと逸脱しているのだが(事前分布をデータで決めているわけだから)、便利な方法だし、実務的な悪影響はない。

　上の式でもっとも高次元なパラメータは、モデル全体の事前情報行列$\Omega^{-1}$である。$\mathbf{x}_t$を$t$行目に積みあげて得られる計画行列を$\mathbf{X}$としよう。通常の回帰モデルの尤度は情報行列$\mathbf{X}^T \mathbf{X} / \sigma^2_e$を持つ。だから、
　$\Omega^{-1} = \kappa \mathbf{X}^T \mathbf{X} /n$
とすれば、事前平均$b$に観察数$\kappa$ぶんの重みを与えたことになる。これがZellnerのg事前分布である [←ぐああああ... わっかんないよう...]。実務的には、$\mathbf{X}$の列の間の完全な共線性に対する防御策が必要となる。フルランクを保証するためには、
　$\Omega^{-1} = \kappa (w \mathbf{X}^T \mathbf{X} + (1-w) diag( \mathbf{X}^T \mathbf{X} ) )/n$
とするとよろしい。我々はデフォルト値として$w=1/2, \kappa=1$を採用している。
　[ふひいいいいい。こんな話を理解するために生まれたわけではないわ！ とにかく情報行列についてうまいこと考えて下さったってことですね、はい、信じます先生]

　まとめよう。spike-and-slab事前分布を使うことで、事前パラメータ$\pi_k, b, \Omega^{-1}, \nu$を通じて事前の意見を簡単に表現することができる。 ある種の合理的想定に頼るというコストを払って単純さを選ぶ分析者は、事前情報を、期待されるモデルサイズ、期待される$R^2$、その推測に与える重みを表すサンプルサイズ$\nu$にまで切り詰めることができる。事前分布について考えること自体を避けたいという分析者のために、我々のソフトはデフォルト値$R^2=0.5, \nu=0.01, \pi_k=0.5$をご用意している。

論文：データ解析(2015-) - 読了：Scott & Varian (2014) ベイジアン構造時系列モデリング

　これは調べ物をしていて偶然見つけた奴なのだが、結果的に、今年読んだなかでもっとも面白い論文であった。ほんとに、読んでみないとわからないものだ。

Guo, F., Blundell, C., Wallach, H., Heller, K. (2015) The Bayesian Echo Chamber: Modeling Social Influence via Linguistic Accomodation. Proceedings of the 18th International Conference on Artificial Intelligence and Statistics (AISTATS). 315-323.
　少人数の会話について語の生成を確率的にモデル化する。逐語録から推定したパラメータに基づき、参加者間の影響関係をネットワークで表現できる。あきらかに私の手には負えないレベルの論文なんだけど、あまりに面白くて、のめりこんで読んでしまった。

1. イントロ
　社会的相互作用のプロセスについてリアリスティックなモデルを構築するためには、その構造(誰が誰に話したか)、内容、時間的ダイナミクスを考慮しなければならない。
　主に関心が持たれるのは「誰が誰に影響したか」である。伝統的には、影響はネットワークのリンクの分析によって研究されてきた。リンクが明示的には存在しなかったり、信頼できなかったり、行動を安定的に反映していなかったりする分野では、影響の代理変数として、観察された相互作用ダイナミクス、すなわちターン・テイキング行動に注目が集まった。

　我々のアプローチは一味違う。ご紹介しよう、「ベイジアン・エコー・チェンバー」です。[以下BCE]
　このモデルは観察された相互作用内容に注目する。社会言語学によれば、2人が相互作用するとき、一方がある語を使用すると、その後他方がその語を使う確率が高まる。この変化は権力の弱いほうの人が強いほうの人に接近する形で生じる。これを言語的調節という(West & Turner, 2010, 書籍)。
　BCEはHawkes過程(後述)とベイジアン言語モデルを結合した動的言語モデルである。BCEモデルは潜在的影響変数を通じた言語的調節を捉える。これらの変数が影響ネットワークを定義し、それによって「誰が誰に影響したか」があきらかになる。

2. ターン・テイキングを通じた影響
　BCEはBlundell, et al. (2012 NIPS)のターン・テイキング・モデルにインスピレーションを受けている。まずはこのモデルを紹介しよう(ただしセッティングはオリジナルと異なる)。
　グループ・ディスカッションのように、複数の参加者がいてどの人の発話も全員に聞こえる場面について考える。
　参加者$p$が観察期間$[0, T)$に行った発話の数を$N^{(p)}(T)$とする。個々の発話にはタイムスタンプ$\mathcal{T}^{(p)} = \{t_n^{(p)}\}_{n=1}^{N^{(p)}(T)}$がつく。個々の発話の持続時間$\Delta t_n^{(p)}$も観察されているとする。よって発話終了時間$t_n^{'(p)} = t_n^{(p)} + \Delta t_n^{(p)}$もわかっている。

　[以下しばらくのあいだ、全く理解不能なのだが、虚心にメモを取る]
　Blundellらのモデルの基盤にあるのはHowkes過程(Hawkes, 1971)である。
　Hawkes過程とは、自己・相互励起型の二重ストカスティック点過程のクラスである(a class of self- and mutually exciting doubly stocastic point processes)。Howkes過程は非等質ポワソン過程(inhomogeneous Poisson process)の一形式であり、条件付きストカスティック速度関数 a conditional stochastic rate function $\lambda(t)$が、時点$t$に先行するすべての事象のタイムスタンプに依存する。
　Blundellらは2つのHawkes過程を組み合わせて二人のターン・テイキングをモデル化しているのだが、ここでは$p$人のディスカッションを表す多変量Hawkes過程を定義しよう。

　期間$[a, b)$を引数にとり、対象者$p$がその間隔のあいだに行う発話の数を返す関数を$n^{(P)}(\cdot)$とする。参加者$p$のHawkes過程のストカスティック速度関数は
　$\lambda^{(p)}(t)$
　$\displaystyle =\lambda_0^{(p)} + \sum_{q \neq p} \int_0^{t^{-}} g^{(qp)} (t,u)d N^{(q)}(u)$
　$\displaystyle =\lambda_0^{(p)} + \sum_{q \neq p} \sum_{n:t_n^{'(q)} < t} g^{(qp)} (t, t_n^{'q})$
ただし$\lambda_0^{(p)}$は参加者$p$の発話のベース速度。$g(t,u)$は非負で定常のカーネル関数で、時点$u < t$におけるある出来事が、時点$t$における即時的速度を増大させる程度、ならびにこの増大の時間的減衰の程度を表す。参加者$p$の速度関数と、他の$P-1$人の人々のHawkes過程とは、他のそれぞれの人のカウンティング指標$\{N^{(q)}(\cdot)\}_{q \neq p}$と、カーネル関数$g(t,u)$によって結びつく。なお、タイムスタンプ$t_n^{'(q)}$は、参加者$q$の$n$番目の発話の終了時間である。従って、$q$によるある発話が$p$の即時的速度を増大させるのは、その発話が完了してからである。
　Bulundellらはカーネル関数として標準的な指数関数
$g^{(qp)}(t,u) = \nu^{(qp)} \exp(-(t-u)/\tau_T^{(p)})$
を使った(別にノンパラメトリックでもよいのだけれど)。ここで$\nu^{(qp)}$は非負のパラメータで、参加者$q$から$p$への即時的励起が生じる程度を表す。ここでの目標は、人々の間の影響関係のモデル化だから、自己励起は0、すなわち$\nu^{(pp)}=0$とする。このパラメータのマトリクスは「誰が次に喋りそうか」「それはいつ起きそうか」のネットワークを表現する。$\tau_T^{(p)}$は対象者$p$の励起が減衰する速度を表す。

　[オーケー。もういいよ。あんたたちがすごく頭がいいことはわかった。俺が頭悪いこともわかった。
　ここまでの話を俺にもわかる程度にざっくり説明すると、こういうことなんじゃなかろうか。
　いまここに、グループ・ディスカッションの逐語録があって、各発話の開始と終了のタイムスタンプが記録されている。発話の内容を無視すると、時間を横軸、累積発話数を時間にとって、個々の対象者の累積発話数の曲線が得られる。
　Blundellたちのアプローチを使うと、この累積発話数曲線を生成するモデル、いいかえれば、個々の対象者の任意の時点での「発話力」みたいなものを生成するモデルを作ることができる。モデルのインプットは、その瞬間までの全員の発話の開始・終了タイムスタンプ。
　このモデルの中にはいくつかパラメータがあるんだけど、その一つが人数x人数の正方行列の形をしたパラメータ行列、つまりは参加者の有向ネットワークであり、リンクの重みは「誰が喋ると誰の発話力が上がるか」を表している。
　ってことですよね？]

3. 言語的調整による影響
　いよいよBECモデルの説明である。

　期間$[0, T)$における参加者$p$の発話数を$N^{(p)}(T)$とする。$V$個のユニークな語タイプがある。参加者$p$の$n$番目の発話は$L_n^{(p)}$個の語トークン$\{w_{1,n}^{(p)}, w_{2,n}^{(p)}, \ldots, w_{L_n^{(p)},n}^{(p)} \}$からなっている。

　個々のトークンの生成過程は、動的ベイジアン言語モデリングと多変量Hawkes過程の両方から得たアイデアに基づいている。
　まず、参加者$p$の$n$番目の発話の$l$番目のトークンは、その発話に対してspecificなカテゴリ分布からドローされる。つまり
　$w_{l,n}^{(p)} \sim Categorical(\phi_n^{(p)})$
ここで$\phi_n^{(p)}$は$V$次元の離散確率ベクトルである。

　次に、確率ベクトル$\phi_n^{(p)}$はディリクレ分布からドローされていて、そのconcentrationパラメータは人にspecific、base measureは発話にspecificである。つまり
　$\phi_n^{(p)} \sim Dirichlet (\alpha^{(p)}, B_n^{(p)})$
concentrationパラメータ$\alpha^{(p)}$は正のスカラーで、分布の分散を決定している。base measure $B_n^{(p)}$は$V$次元の離散確率ベクトルで、分布の平均を決定している。
　[ここでまた疑問符で頭がいっぱいに...
　ふつう、$V$次元のディリクレ分布のパラメータはひとつで、それは$V$次元の正値ベクトルで、これを集中度と呼ぶと思う。でもこの論文では、ディリクレ分布のパラメータが集中度$\alpha^{(p)}$とベース尺度$B_n^{(p)}$の2つにわかれ、前者を個人レベルのパラメータ、後者を発話レベルのパラメータとしている。次の段落に出てくるように、後者には和が1という制約を掛けている。あてずっぽうだけど、おそらく$\alpha^{(p)} B_n^{(p)}$が通常の表現でいうところのディリクレ分布のパラメータなのだろう]

　$B_n^{(p)}$は以下の条件を満たすものとする。
　$B_{v,n}^{(p)} \propto \beta_v^{(p)} + \sum_{q \neq p} \rho^{(qp)} \phi_{v,n}^{(qp)}$
　$\sum_{v=1}^{V} B_{v,n}^{(p)} = 1$
$V$次元の正値ベクトル$\beta_v^{(p)}$は、参加者$p$に固有な言語使用を表す。$\rho^{(qp)}$は非負のパラメータで、参加者$q$が参加者$p$に与える言語的励起の程度を表す。自己励起はなし、すなわち$\rho^{(pp)} = 0$とする。最後に、$\phi_{v,n}^{(qp)}$は$V$次元の正値ベクトルで
　$\displaystyle \phi_{v,n}^{(qp)} = \sum_{m:t_m^{'(q)} < t_n^{(p)}} \left( \sum_{l=1}^{L_m^{(q)}} 1(w_{l,m}^{(q)} = v) \right) \times \exp \left( -\frac{t_n^{(p)}-t_m^{'(q)}}{\tau_L^{(p)}}\right)$
　[こういうのはビビっては負けだ。順に見ていこう。
　内側のサメーションの右側$1(w_{l,m}^{(q)} = v)$は、「参加者$q$の$m$番目の発話の$l$番目の語が$v$だった」。
　内側のサメーションは「参加者$q$の$m$番目の発話における語$v$の出現個数」。
　それに掛けているのは、「参加者$q$の$m$番目の発話の終了時間から、参加者$p$の$n$番目の発話開始時間までの経過時間を、参加者$p$が持つ謎のパラメータ$\tau_L$で割って負にして指数をとったもの」で、直後であれば1, 時間経過とともに0に近づく。つまり、参加者$q$の$m$番目の発話が与える影響を経過時間にともなって指数的に減衰させており、その減衰の強さが$\tau_L$なのである。
　最後に、外側のサメーションは、以上を「参加者$q$の発話のうち、参加者$p$の$n$番目の発話が始まる前に終わった奴すべて」について合計している。
　つまり$\phi_{v,n}^{(qp)}$は、おおざっぱにいえば「参加者$p$の$n$番目の発話までに、参加者$q$が単語$v$を使った程度」を表しているわけだ。
　なるほどね、いっけんややこしいけど、実は素直なモデリングだ]

　以上をまとめると、推定すべきパラメータは以下となる。参加者$p$について、
　$\alpha^{(p)}$: スカラー。ディリクレ分布の分散を表す。
　$\beta^{(p)}$: $V$次元ベクトル。この参加者に固有な言語使用を表す。
　$\{\rho^{(qp)}\}_{q \neq p}$: スカラー。他の参加者$q$が言語的調整を引き起こす程度。
　$\tau_L^{(p)}$: スカラー。言語的調整の減衰の程度。
　パラメータ推定の方法は...[略。collapsed slice-within-Gibbs samplingというのを使うのだそうだ。知らんがな]

　[あーっ！！！いま気が付いた！
　BECモデルは発話の発生時間はモデル化しないんだ！ Hawkes過程ってのは発想を説明するために登場しただけで、BECモデル自体はHawkes過程についてなにも知らなくても、普通の言語生成モデルとして理解できるんじゃないですか、これ？！
　うわぁー。びびって損した... 俺には絶対理解できない論文なんじゃないかと思っちゃったよ...]

4. 関連研究　[ここは詳しくメモする]
　時間的ダイナミクスから影響関係やその他の社会的関係を推論する確率過程のモデルとして以下が挙げられる。中心となっているのはHawkes過程である。

相互作用の内容もモデルに入れる研究としては:

本研究のポイントは、言語的調整からの推論とターンテイキングからの推論を比較するところ、生成モデルをつくるところ。

5. 実験 [ここはめくっただけ]

　人工データを使ってパラメータが復元できるかどうかを試した。うまくいきました。

　米最高裁の審理の３つのトランスクリプト、映画「12人の怒れる男」のトランスクリプト、連邦公開市場委員会(FOMC)の会議32回分のトランスクリプトを分析した。
　[以下略。ちゃんと読んでないんだけど、「12人の怒れる男」の参加者間ネットワークはなんだかそれっぽい感じで面白かった。Blundellらのターンテイキングの分析ではこうはうまくいかないとのこと。これ、三谷幸喜「12人の優しい日本人」で試してみたいなあ...]

　ためしに、BlundellらのモデルとBECモデルを結合してみた。すなわち、$\rho^{(qp)} = rv^{(qp)}$として同時に推定した。結果、ホールドアウトへの事後確率は低下した。推定されたパラメータはBECのそれとそっくりだった。おそらく、ターンテイキングにおける参加者間の影響より、言語的調整のほうがより情報豊かなのであろう。

6. 考察
　今後の課題：(1)語の機能や内容別に言語的調整をモデリングする。(2)影響ネットワークの動的変化を陽にモデル化する。[←どっちも面白そう]

　... いやー、おおかた私の能力を超える内容ではあるのだが、それにしても超・面白かった。集団での議論って、ある人が議論をリードしているとき、その人が繰り出す単語がその後の全員の発話の土俵になったりするじゃあないですか。このモデルではこの現象を、対象者間の影響関係のネットワークとして視覚化できるわけだ。
　あんまり詳しく書けないけど、私自身の仕事ともものすごく関係する話である。読み終えてからの後知恵だけど、そうそう！こういう研究がないかなあと思ってたんだよ！という内容であった。

　どうせなら、ネットワークが動的に変わっていけば超面白いのに。で、「振り返るとあの構造変化は、あの人が繰り出したあの発言のあの単語のせいだった」なんてことが定量化できたら、これはめちゃくちゃ面白いのに。
　... とメモを取りながら気が付いたけど、そういう動的可視化の面白さだけを求めるならば、別に苦労して生成的確率モデルを作ってパラメータをまじめに推定しなくても、もう少し簡便な方法があるかもしれない。考えてみよう。

論文：データ解析(2015-) - 読了：Guo, Blundell, Wallach, Heller (2015) ベイジアン・エコー・チェンバー

Bookcover THIS IS JAPAN――英国保育士が見た日本 [a]
ブレイディ みかこ / 太田出版 / 2016-08-17

Bookcover 宝くじで1億円当たった人の末路 [a]
鈴木 信行 / 日経BP / 2017-03-25
面白いコンセプトの本だとは思うんだけど... ビジネス誌連載だけあって、妙に説教くさい内容であった。

ノンフィクション(2011-) - 読了：「THIS IS JAPAN 英国保育士が見た日本」「宝くじで1億円当たった人の末路」

Bookcover 美少女美術史: 人々を惑わせる究極の美 (ちくま学芸文庫) [a]
英洋, 池上,咲紀, 荒井 / 筑摩書房 / 2017-06-06

Bookcover 舞台をまわす、舞台がまわる - 山崎正和オーラルヒストリー [a]
山崎 正和 / 中央公論新社 / 2017-03-21

Bookcover 全裸監督 村西とおる伝 [a]
本橋 信宏 / 太田出版 / 2016-10-18

Bookcover 恋愛を数学する (TEDブックス) [a]
ハンナ・フライ / 朝日出版社 / 2017-02-21

Bookcover ロベスピエール [a]
ピーター・マクフィー / 白水社 / 2017-02-25

ノンフィクション(2011-) - 読了：「美少女美術史 人々を惑わせる究極の美」「舞台をまわす、舞台がまわる 山崎正和オーラルヒストリー」「全裸監督 村西とおる伝」「恋愛を数学する」「ロベスピエール」

Bookcover 「Gゼロ」後の世界―主導国なき時代の勝者はだれか [a]
イアン・ブレマー / 日本経済新聞出版社 / 2012-06-23

Bookcover 抗うニュースキャスター [a]
金平 茂紀 / かもがわ出版 / 2016-09-16

Bookcover 聞書き 遊廓成駒屋 (ちくま文庫) [a]
宣武, 神崎 / 筑摩書房 / 2017-01-10

Bookcover 増補 モスクが語るイスラム史: 建築と政治権力 (ちくま学芸文庫) [a]
正, 羽田 / 筑摩書房 / 2016-12-07

Bookcover シェイクスピア・カーニヴァル (ちくま学芸文庫) [a]
コット,ヤン / 筑摩書房 / 2017-02-08

ノンフィクション(2011-) - 読了：「「Gゼロ」後の世界 主導国なき時代の勝者はだれか」「抗うニュースキャスター」「聞書き 遊郭成駒屋」「増補 モスクが語るイスラム史 建築と政治権力」「シェイクスピア・カーニヴァル」

Bookcover 社会学入門―人間と社会の未来 (岩波新書) [a]
見田 宗介 / 岩波書店 / 2006-04-20

Bookcover プロテスタンティズム - 宗教改革から現代政治まで (中公新書) [a]
深井 智朗 / 中央公論新社 / 2017-03-21

Bookcover 身近な自然の観察図鑑 (ちくま新書1251) [a]
盛口 満 / 筑摩書房 / 2017-04-05

ここからは単行本。

Bookcover 日本会議をめぐる四つの対話 [a]
菅野 完,村上 正邦,魚住 昭,横山 孝平,白井 聡 / ケイアンドケイプレス / 2016-12-11

Bookcover ギリシャ危機と揺らぐ欧州民主主義――緊縮政策がもたらすEUの亀裂 [a]
尾上 修悟 / 明石書店 / 2017-03-10
本というのは読んでみないとわからないもので、私のような門外漢にも大変考えさせられる本であった。日本の明日と重ねて読み耽った次第。

ノンフィクション(2011-) - 読了：「社会学入門 人間と社会の未来」「プロテスタンティズム 宗教改革から現代政治まで」「身近な自然の観察図鑑」「日本会議をめぐる四つの対話」「ギリシャ危機と揺らぐ欧州民主主義 緊縮政策がもたらすEUの亀裂」

Bookcover シリーズ<本と日本史> 3 中世の声と文字 親鸞の手紙と『平家物語』 (集英社新書) [a]
大隅 和雄 / 集英社 / 2017-01-17

Bookcover ルポ 絶望の韓国 (文春新書) [a]
愛博, 牧野 / 文藝春秋 / 2017-05-19

Bookcover ドキュメント 日本会議 (ちくま新書1253) [a]
藤生 明 / 筑摩書房 / 2017-05-09

Bookcover 偽りの経済政策――格差と停滞のアベノミクス (岩波新書) [a]
服部 茂幸 / 岩波書店 / 2017-05-20

Bookcover 自民党―「一強」の実像 (中公新書) [a]
中北 浩爾 / 中央公論新社 / 2017-04-19

ノンフィクション(2011-) - 読了：「中世の声と文字 親鸞の手紙と「平家物語」」「ルポ 絶望の韓国」「ドキュメント 日本会議」「偽りの経済政策 格差と停滞のアベノミクス」「自民党 「一強」の構造」

Bookcover 東芝解体 電機メーカーが消える日 (講談社現代新書) [a]
大西 康之 / 講談社 / 2017-05-17

Bookcover 未来の年表 人口減少日本でこれから起きること (講談社現代新書) [a]
河合 雅司 / 講談社 / 2017-06-14

Bookcover 弘法大師空海と出会う (岩波新書) [a]
川崎 一洋 / 岩波書店 / 2016-10-21

Bookcover 貧困と地域 - あいりん地区から見る高齢化と孤立死 (中公新書) [a]
白波瀬 達也 / 中央公論新社 / 2017-02-19

Bookcover バッタを倒しにアフリカへ (光文社新書) [a]
前野ウルド浩太郎 / 光文社 / 2017-05-17

ノンフィクション(2011-) - 読了：「東芝解体 電機メーカーが消える日」「未来の年表 人口減少日本でこれから起きること」「弘法大師空海と出会う」「貧困と地域 あいりん地区から見る高齢化と孤立死」「バッタを倒しにアフリカへ」

Bookcover シリア情勢――終わらない人道危機 (岩波新書) [a]
青山 弘之 / 岩波書店 / 2017-03-23

Bookcover 新しい幸福論 (岩波新書) [a]
橘木 俊詔 / 岩波書店 / 2016-05-21

Bookcover ロシア革命――破局の8か月 (岩波新書) [a]
池田 嘉郎 / 岩波書店 / 2017-01-21

Bookcover 経済学のすすめ－人文知と批判精神の復権 (岩波新書) [a]
佐和 隆光 / 岩波書店 / 2016-10-20

Bookcover パウロ 十字架の使徒 (岩波新書) [a]
青野 太潮 / 岩波書店 / 2016-12-21
まさかの面白本。パウロさん、いろいろ大変だったんだなあ、と...

ノンフィクション(2011-) - 読了：「シリア情勢 終わらない人道危機」「新しい幸福論」「ロシア革命 破局の8か月」「経済学のすすめ 人文知と批判精神の復権」「パウロ 十字架の使徒」

Bookcover 応仁の乱 - 戦国時代を生んだ大乱 (中公新書) [a]
呉座 勇一 / 中央公論新社 / 2016-10-19

Bookcover 日本と中国経済: 相互交流と衝突の100年 (ちくま新書1223) [a]
梶谷 懐 / 筑摩書房 / 2016-12-06

Bookcover ルポ 難民追跡――バルカンルートを行く (岩波新書) [a]
坂口 裕彦 / 岩波書店 / 2016-10-21

Bookcover 夏目漱石 (岩波新書) [a]
十川 信介 / 岩波書店 / 2016-11-19

Bookcover ルポ トランプ王国――もう一つのアメリカを行く (岩波新書) [a]
金成 隆一 / 岩波書店 / 2017-02-04

ノンフィクション(2011-) - 読了：「応仁の乱 戦国時代を生んだ大乱」「日本と中国経済 相互交流と衝突の100年」「ルポ 難民追跡 バルカンルートを行く」「夏目漱石」「ルポ トランプ王国 もう一つのアメリカを行く」

最近読んだ本。記録をさぼっていたので随分溜まってしまった。まずは新書から。

Bookcover フィリピンパブ嬢の社会学 (新潮新書) [a]
中島 弘象 / 新潮社 / 2017-02-16
これは本当に面白い本だった。読み終えたときにメモしとかんといかんな。

Bookcover トランプが戦争を起こす日 悪夢は中東から始まる (光文社新書) [a]
宮田 律 / 光文社 / 2017-03-16

Bookcover 「天皇機関説」事件 (集英社新書) [a]
山崎 雅弘 / 集英社 / 2017-04-14

Bookcover 通貨の日本史 - 無文銀銭、富本銭から電子マネーまで (中公新書) [a]
高木 久史 / 中央公論新社 / 2016-08-18

Bookcover 日本人なら知っておきたい 四季の植物 (ちくま新書1243) [a]
湯浅 浩史 / 筑摩書房 / 2017-03-06
なんだか変な題名だなあ...

ノンフィクション(2011-) - 読了：「フィリピンパブ嬢の社会学」「トランプが戦争を起こす日 悪夢は中東から始まる」「「天皇機関説」事件」「日本人なら知っておきたい四季の植物」「通貨の日本史 無文銀銭、富本銭から電子マネーまで」

Zallar, J., & Feldman, S. (1992) A simple theory of the survey response: Answering questions versus revealing preferences. American J. Political Science, 36(3), 579-616.

　原稿の準備で読んだ論文。経緯は忘れたが「必ず読むこと」論文の山に積んであった。政治学の論文だけど、それにしてもずいぶん魅力的な題名である。Google Scholar的には引用回数1500超、結構なメジャー論文だ。

　いわく。
　市民は政治問題についてなんらかの態度を形成している。質問紙調査はそれらの態度の受動的な測定である。という標準的な見方を乗り越え、新しい見方を提供しましょう。すなわち、市民は態度なんて持ってない。頭のなかにあるのはいろんなideaやconsiderationであり、それらは部分的に整合していたり、不整合だったりする。調査参加者は回答に際してそれらをサンプリングし(ここに最近の出来事や調査票の影響が加わる)、どう答えるかをその場で決める。つまり、回答は真の態度なんて反映していない。

　先行研究概観。

　しかるに世論調査研究者ときたら、これらの研究を無視し、伝統的見解をつぎはぎして乗り切ろうとしておる。時系列調査では調査の設問順を変えないようにしましょうとか、項目順をランダマイズしましょうとか。測定誤差を統計的に取り除きましょうとか。[←ははは]

　調査対象者は本当はどうやって回答しているのか？ 2系統の研究がある。

　では、さまざまなconsiderationsはどのように回答へと変換されるか。

　まとめよう。(以下でわざわざconsiderationという言葉を使っているのは、政治についての日常言語に近いから、そしてスキーマと違って心的構造・処理への含意がないから)

　ここからは実証研究。
　National Election Studies(NES)というのがあって、1987年にそのパイロット・スタディーとして電話調査をやった。2ウエーブ、計約800人。[これは延べ人数で、どうやら2回答えた人もいるらしい]
　NESの設問(3問、強制選択)と自由記述の組み合わせ。対象者を2条件にランダムに割り当てる。形式A(回顧プローブ)では、NESの設問に回答してもらったのち(強制選択)、いま答えた時に思い浮かんだことを教えてください、とオープンエンドで聴取。形式B(stop-and-thinkプローブ)では、NESの設問を読み上げ、いま思い浮かんだことを訊き、設問文を再度読み上げて回答してもらう。自由記述はコーディングする。
　結果。

　考察。
　今後の研究課題：

　最後に、このモデルの規範的な含意について。かつてConverseは「あのな、大衆に態度なんかあらしまへんで」と述べ、Achenは「そんなことゆうたら民主主義理論はなりたちませんがな」と反論した[←意訳]。我々の理論はこの中間に位置し、調査結果の解釈を拡張する。調査結果とは人々のconsiderationのバランスを示すものなのだ。云々、云々。

　... 正直言って、実証研究のところからつまんなくなってほとんど読み飛ばしちゃったんだけど、序盤の理論提示のところがとても面白かった。この種の話のもっと新しい議論にキャッチアップしたいのだが、うーん、どうすればいいのかしらん。

　この論文を机の横に積んでいた経緯はいまいち思い出せないんだけど、たぶんSnidermanを引用している論文を片っ端から探しているときにみつけたのだと思う。えーと、最後の考察の「研究者たちは多くの場合、態度という言葉を、多かれ少なかれ結晶化したもの、多かれ少なかれイデオロギー的なもの、ないし人や問題を通じた異質性のあるものを指して用いてきた」というところで、Sniderman, Brody, & Tetlock (1991, 書籍)が引用されている。どういう文脈での引用なのかいまいちわからん。

論文：調査方法論 - 読了：Zallar & Feldman (1992) 調査は「真の態度」の測定ではない、むしろアイデアのサンプリングだ

2017年8月17日 (木)

Prelec, et al.(2017, Nature) の自分向け徹底解説、最終回。前回は、世界の数と知識の状態の数が等しいとき、回答から正解を導く方法が示された。今回はこれを、世界の数と知識の状態の数が異なる場合へと一般化する部分である... はずだ。

前回までのあらすじ
　いまここに$m$個の可能世界がある。私たちはどの世界が現実なのかを知らない。そこで、$m$個の選択肢を提示し、いずれが正しいと思うかを人々に投票させる。その結果に基づき、どの可能世界が現実かを同定したい。

世界が3つ以上、シグナルが2つの場合

　以下では、世界が3つ以上、シグナルは2つの場合について考える。ここでは、シグナルは偏りのあるコインのトスのようなものである。

　ある$a_i$について、ベイズの定理より、
　$Pr(S = s_1 | A = a_i) = Pr(A = a_i | S = s_1) Pr(S=s_1) / Pr(A=a_i)$
　$Pr(S = s_2 | A = a_i) = Pr(A = a_i | S = s_2) Pr(S=s_2) / Pr(A=a_i)$
比をとって
　$\displaystyle \frac{Pr(S = s_1 | A = a_i)}{Pr(S = s_2 | A = a_i)}$
　$\displaystyle = \frac{Pr(A = a_i | S = s_1) Pr(S=s_1)}{Pr(A = a_i | S = s_2) Pr(S=s_2)}$
分子と分母を$P(S=s_1)P(S=s_2)$で割って
　$\displaystyle = \frac{Pr(A = a_i | S = s_1) /Pr(S=s_2)}{Pr(A = a_i | S = s_2) /Pr(S=s_1)}$
分子と分母に$Pr(S^q = s_1, S^r=s_2)=Pr(S^q = s_2, S^r=s_1)$を掛けて
　$\displaystyle = \frac{Pr(A = a_i | S = s_1) Pr(S^q = s_1, S^r=s_2)/Pr(S=s_2)}{Pr(A = a_i | S = s_2)Pr(S^q = s_2, S^r=s_1) /Pr(S=s_1)}$
　$\displaystyle = \frac{Pr(A = a_i | S = s_1) Pr(S^q = s_1 | S^r=s_2)}{Pr(A = a_i | S = s_2)Pr(S^q = s_2 | S^r=s_1)}$
つまり、私たちはコインの偏りそのものは知らないけれど、世界についての事後確率とペアワイズの予測を通じて、コインの偏りを推測することはできるわけである。

　対象者に自分のコイントスの結果を報告してもらうとしよう。その結果は、$Pr(S=s_1|a_{i*})$と$Pr(S=s_2|a_{i*})$に収束するだろう。従って
　$\displaystyle i = i* \Leftrightarrow \frac{Pr(A = a_i | S = s_1) Pr(S^q = s_1 | S^r=s_2)}{Pr(A = a_i | S = s_2)Pr(S^q = s_2 | S^r=s_1)} = \frac{Pr(S=s_1|a_{i*})}{Pr(S=s_2|a_{i*})}$

[ちょっ、ちょっと待って! これは定理2や定理3とどういう関係にあるの？ 同じことを言っているの、それとも違う話なの?! わからなーい...]

[ここから逐語訳...]

具体例を挙げよう。3枚のコインを想定する。アプリオリには等しくもっともらしい。(A) 2:1でオモテが出やすいコイン。(B) 2:1でウラが出やすいコイン。(C) 偏りのないコイン。
　実際のコインは(C)だとしよう。対象者は、自分のトス、(A)(B)(C)の事後確率、トスの予測分布を報告する。トスの報告は表と裏が五分五分となる結果に収束する。そこから、分析者は実際のコインが偏りのないコインであることを学ぶ。しかし、(A)(B)(C)のどれが偏りのないコインなのかを分析者はまだ知らない。[←ここの意味がわからない...]
　対象者は、自分のトスにベイズの規則を適用し、事後確率を引き出して報告する。トスが表であった対象者にとっての(A)(B)(C)の事後確率は(4/9, 2/9, 1/3)であり、トスが裏であった対象者にとっての(A)(B)(C)の事後確率は(2/9, 4/9, 1/3)である。この情報によって、いまや分析者は(A)(B)(C)の正確な事後分布を知る。しかし、定理1が示しているように、こうした事後確率分布としてどんな分布が手に入ったとしても、それは3種類のコインのどれとでも整合可能である。
　ここで、予測を付け加えることで現実世界を同定できる。上の例の場合、想定が対称的であるから、対象者の予測もまた対称的である。すなわち$p(s_j|s_k)=p(s_j|s_k)$である[←これ、なにかの誤植じゃないかなあ...]。予測と事後確率に基づき、分析者はそれぞれの可能なコインのバイアスを計算できる。ここで、コイン(C)は偏りのないコインであり、計算されたバイアスと実際のバイアスが一致する唯一のコインである。従って分析者は、実際のコインは(C)に違いないと演繹する。

[すいません、逐語訳しましたが、やっぱりわかりません... 話の主旨はわかるが、定理2, 定理3との関係がつかめない]

世界が3つ以上、シグナルが3つ以上

同じ方法が、シグナルが2つよりも多い一般的な場合にもあてはまる。しかし、elicitationがシグナルと世界の可能な状態と分離するという点が重要である。対象者はシグナルを報告し、シグナルを予測し、世界の状態に事後確率を付与する。

...というわけで、Prelec, et al. (2017) のSupplementary Informationを四回にわたってゆっくり読み進めてきたのだが、大変残念なことに、第四回の後半から途方に暮れた。一行一行は理解できるのだが、話の流れがつかめないのである。能力が足りないと云わざるを得ない。哀しい。
　ま、ほとぼりが冷めたら、また読み直してみよう。ないし、誰かが私レベルに向けてわかりやすく解説して下さるのを待とう。

雑記：データ解析 - 「みんなが思うよりも意外に多い」回答はなぜ正しいか：その4

Prelec, et al.(2017, Nature) の自分向け徹底解説、第三回。前回は、世界が2つ、知識の状態が2つ以上の場合に「みんなが思うよりも意外に多い回答は正しい」ことが示された。今回は、これを世界が3つ以上の場合へと一般化する部分である。

前回までのあらすじ
　いまここに$m$個の可能世界がある。私たちはどの世界が現実なのかを知らない。そこで、$m$個の選択肢を提示し、いずれが正しいと思うかを人々に投票させる。その結果に基づき、どの可能世界が現実かを同定したい。

補題

補題. $m$個の答え、$n$個のシグナル、同時分布$p(S=s_j, A=a_i)$からなる、ある可能世界モデルについて考える。正解を$a_{i*}$とすると、
　$\displaystyle Pr(A=a_{i*}|S=s_k) \propto Pr(S=s_k|A=a_{i*}) \sum_i \frac{Pr(S^q=S_i|S^r=s_k)}{Pr(S^q=S_k|S^r=s_i)}$
　ただし$0 / 0 \equiv 0$。

証明。任意の2名$r, q$のシグナルの同時分布について考える。
　$Pr(S^q=s_k, S^r=s_i) = Pr(S^q=s_k|S^r=s_i)P(S^r=s_i)$
　$Pr(S^q=s_i, S^r=s_k) = Pr(S^q=s_i|S^r=s_k)P(S^r=s_k)$
$r$と$q$のシグナルを入れ替えても確率は同じ、すなわち$Pr(S^q=s_k, S^r=s_i)=Pr(S^q=s_i, S^r=s_k)$だから、上の2本の式の右辺は等しく
　$Pr(S^q=s_k|S^r=s_i)P(S^r=s_i) = Pr(S^q=s_i|S^r=s_k)P(S^r=s_k)$
移項する。$P(S^r=s_i)$は$r$を$q$に書き換えても同じことだから$P(S=s_i)$ と略記して、
　$\displaystyle P(S=s_i) = P(S=s_k)\frac{Pr(S^q=s_i|S^r=s_k)}{Pr(S^q=s_k|S^r=s_i)}$
両辺を$i$を通じて合計すると、左辺の合計は1になるから、
　$P(S=s_k) = \left( \sum_i \frac{Pr(S^q=s_i|S^r=s_k)}{Pr(S^q=s_k|S^r=s_i)} \right)^{-1}$
これを(1)とする。

　さて、ベイズの定理から
　$Pr(A=a_{i*}|S=s_k)$
　$\displaystyle = \frac{p(S=s_k | A=a_{i*}) Pr(A=a_{i*})}{Pr(S=s_k)}$
(1)を分母に代入して
　$\displaystyle = Pr(S=s_k|A=a_{i*}) \sum_i \frac{Pr(S^q=S_i|S^r=s_k)}{Pr(S^q=S_k|S^r=s_i)} Pr(A=a_{i})$
ここで$Pr(A=a_{i})$は$k$を通じて定数だから、補題が成り立つ。証明終。

　この補題が示しているのはこういうことだ。シグナルの分布$Pr(S=s_k|A=a_{i*})$と、シグナルのペアワイズ予測$Pr(S^q=S_i|S^r=s_k), Pr(S^q=S_k|S^r=s_i)$から、もっともinformedな回答者たちが支持する答えを特定できる。ここでinformedというのは、正解に最大の確率を付与しているという意味である。それらの対象者は、仮に正解が明らかになったとしてもっとも驚かない人々である。
　[いやー、ここ、難しい。証明自体は納得できるけど、式がなにを意味しているのかがつかみにくい。我慢して先に進もう]

定理3

$m=n, V(S=s_i) = v_i, Pr(A=a_i | S=s_i) > Pr(A=a_i | S=s_j)$とする。正解を$a_{i*}$とする。答え$a_k$への予測規準化投票$\bar{V}(k)$を以下のように定義する。
　$\displaystyle \bar{V}(k) = Pr(V = v_k | A = a_{i*}) \sum_i \frac{Pr(V^q = v_i|S^r=s_k)}{Pr(V^q=v_k|S^r=s_i)}$
ただし。$0 / 0 \equiv 0$。このとき、正解は、もっとも高い予測規準化投票を持つ答えである。

証明。$V(S=s_i)=v_i$だから、補題
　$\displaystyle Pr(A=a_{i*}|S=s_k) \propto Pr(S=s_k|A=a_{i*}) \sum_i \frac{Pr(S^q=S_i|S^r=s_k)}{Pr(S^q=S_k|S^r=s_i)}$
は以下のように書き換えることができる。
　$\displaystyle Pr(A=a_{i*}|S=s_k) \propto Pr(V^r=v_k|A=a_{i*}) \sum_i \frac{Pr(V^q=v_i|S^r=s_k)}{Pr(V^q=v_k|S^r=s_i)} = \bar{V}(k)$
　さて左辺について、
　$Pr(A=a_i | S=s_i) > Pr(A=a_i | S=s_j)$
より
　$Pr(A=a_{i*} | S=s_{i*}) > Pr(A=a_{i*} | S=s_k)$
である。よって$\bar{V}(i*) > \bar{V}(k)$である。証明終。

　対象者数が無限大の時、$Pr(V=v_k | A=a_{i*})$は$a_k$への投票の割合である。また、$Pr(V^q=v_k | S^r=s_i)$は、$a_i$に投票した人々による「何割の人が$a_k$に投票するか」予測の平均である。

　[こうしてゆっくり読んでみると、定理3の証明に、定理2は使われてないんですね。
　定理3が定理2の一般化なのだとしたら、$m=n=2$の場合には、定理2と定理3は同じことを意味しているのだろうか。つまり、
　$Pr(V = v_1 | A = a_{i*}) \left(1+ \frac{Pr(V^q = v_2|S^r=s_1)}{Pr(V^q=v_1|S^r=s_2)} \right) > Pr(V = v_2 | A = a_{i*}) \left(1+ \frac{Pr(V^q = v_1|S^r=s_2)}{Pr(V^q=v_2|S^r=s_1)} \right) $
　は
　$Pr(V^q= v_1 | S^r = s_j) \leq Pr(V=v_1 | A=a_{i*})$ for any $j$
と同値なのか。式をあれこれ変形してみたのだが、どうも同値ではないような気がしてならない... 数学ができないとは悲しいもので、残念ながらどこかでなにかを間違えているような気もする。なんだか疲れちゃったので、また日を改めてチャレンジしたい]

雑記：データ解析 - 「みんなが思うよりも意外に多い」回答はなぜ正しいか：その3

Prelec, et al.(2017, Nature) の自分向け徹底解説、第二回。「意外に一般的」原理、すなわち「みんなが思うよりも意外に多い」回答は正しいということを最初に示す、この論文のキモになる部分である。

前回までのあらすじ
　いまここに$m$個の可能世界がある。私たちはどの世界が現実なのかを知らない。そこで、$m$個の選択肢を提示し、いずれが正しいと思うかを人々に聴取し、その回答から、どの可能世界が現実かを同定したい。

　さあ、今回はどんなややこしい話が待ち受けているでしょうか。元気を出して行ってみよう！！！

新たなるセッティング

　対象者$r$の、「いずれが正しいと思うか」投票を$V^r = V(S=S^r)$とする。$V^r$は値として$\{v_1, \ldots, v_m \}$をとる。

　対象者の投票はシグナルの関数だから、シグナル$s_k$を受け取った理想的対象者$r$は、他の対象者$q$が$a_i$に投票する条件つき確率$Pr(V^q=v_i | S^r=s_k)$を算出できる。

　その算出方法の例を挙げよう。いま、シグナル$s_j$を受け取った人は、可能世界のなかから条件つき確率$p(a_i | s_j)$が最大である可能世界を選びその可能世界に投票するのだとしよう。すなわち
　$V(S=s_j) = argmax_i Pr(A=a_i | S=s_j)$
　この場合、他の対象者$q$が$a_i$に投票する条件つき確率$Pr(V^q=v_i | S^r=s_k)$は、$a_i$への投票につながるような証拠を$q$が受け取る確率の合計である。すなわち
　$Pr (V^q = v_i | S^r = s_k)$
　$\displaystyle = \sum_{j: V(s_j) = v_i} Pr(S^q=s_j | S^r=s_k)$
　$\displaystyle = \sum_{i = argmax_k Pr(A=a_k | S=s_j)} Pr(S^q=s_j | S^r=s_k) $

[落ち着け、ここはそんなにヤヤコシイことは言っていない。要するに、もし「人々はどういうシグナルを受け取るとどういう投票をするのか」がわかっているなら、自分が受け取ったシグナルから世界についての事後分布を求め、他人が受け取ったシグナルについての事後分布を求め、他人の投票についての事後分布を求めることが出来るはずだよね、という話だ。2行目のサメーションのインデクスに出てくる$k$は、項のなかに出てくる$k$とは別の記号だと思う]

　同様に、ある人の投票と可能世界との同時確率も定義できる。
　$Pr(V=v_i, A=a_k) = \sum_{j: V(s_j) = v_i} Pr(S=s_j, A=a_k)$
[原文では右辺は$\sum p(s_j, a_j)$だが、$a_j$は$a_k$の誤植だと考え書き換えた]

「意外に一般的」原理：世界が2つ、シグナルが2つ以上の場合

　以下では、世界は2つ、シグナルは2つ以上の場合について、「みんなが思うよりも意外に多い回答は正しい」ことを証明する。

　上では簡単な投票ルール
　$\displaystyle V(s_j) = argmax_i p(A=a_i | S=s_j)$
を考えたが、もうちょっと一般化しよう。

　世界を2つとし、各世界に対するカットオフ $c_1, c_2$(合計1)を考えて
　$\displaystyle V(s_j) = argmax_i c^{-1}_i Pr(A=a_i | S=s_j)$
とする。$c_1=c_2=0.5$だったらさっきの投票ルールと同じである。

定理2. 全員が正解に投票するわけではないとしよう。このとき、正解に対する投票の平均推定値は過小評価される。

　[つまり、島根が西にある世界においては、「島根が西」への他人の投票の推測は過小評価される]

　証明：(まずは原文を逐語的にメモする)

We first show that actual votes for the correct answer exceed conterfactual votes for the correct answer, $p(v_{i*}|a_{i*}) > p(v_{i*}|a_k) , k \neq i*$, as:

　$\displaystyle \frac{p(v_{i*}|a_{i*})}{ p(v_{i*}|a_k)}= \frac{p(a_{i*}|v_{i*}) p(a_k)} {p(a_k|v_{i*}) p(a_{i*})}= \frac{p(a_{i*}|v_{i*})} {1- p(a_{i*}|v_{i*}) } \frac{1-p(a_{i*})}{ p(a_{i*}) }$

The fraction on the right is well defined as $0 < p(a_{i*}|v_{i*}) < 1$; it is greater than one if and only if $p(a_{i*}|v_k) > p(a_{i*}|v_{i*}) p( v_{i*} ) + p(a_{i*}|v_k) p( v_k ) = p(a_{i*})$, as $p(a_{i*}|v_{i*}) > c_{i*}, p(a_{i*}|v_k) < c_{i*}$ by definition of the criterion based voting function.

　[深呼吸してゆっくり考えましょう。
　表記を簡単にするために、仮に$a_1$が現実(原文の$a_{i*}$), $a_2$が反事実(原文の$a_k$)だということにする。
　著者らが上記部分でいわんとしているのは、「現実のもとで現実に投票する確率は、反事実のもとで現実に投票する確率よりも大きい」、すなわち
　$Pr(V=v_1 | A=a_1) > Pr(V=v_1|A=a_2)$
ということだ。なぜか。

　条件付き確率の定義から、
　$\displaystyle Pr(V=v_1 | A=a_1) = \frac{Pr(V=v_1 , A=a_1)}{Pr(A=a_1)} = \frac{Pr(A=a_1 | V=v_1) Pr(V=v_1)}{Pr(A=a_1)}$
　$\displaystyle Pr(V=v_1 | A=a_2) = \frac{Pr(V=v_1 , A=a_2)}{Pr(A=a_2)} = \frac{Pr(A=a_2 | V=v_1) Pr(V=v_1)}{Pr(A=a_2)} $
であるから、
　$\displaystyle \frac{Pr(V=v_1 | A=a_1)}{ Pr(V=v_1 | A=a_2) } = \frac{Pr(A=a_1 | V=v_1) Pr(A=a_2)}{Pr(A=a_2 | V=v_1) Pr(A=a_1)} $
である。$P= Pr(A=a_1 | V=v_1), Q= Pr(A=a_1) $と置けば
　$\displaystyle = \frac{P(1-Q)}{(1-P)Q}$
である。
　いま
　$\displaystyle \frac{P(1-Q)}{(1-P)Q} > 1$
を解くと$P > Q$である。従って、
　$Pr(V=v_1 | A=a_1) > Pr(V=v_1|A=a_2) \Leftrightarrow Pr(A=a_1 | V=v_1) > Pr(A=a_1)$
である。これを(1)としよう。

　$Pr(A=a_1)$を投票で場合分けすると
　 $Pr(A=a_1) = Pr(A=a_1 | V=v_1) Pr(V=v_1) + Pr(A=a_1 | V=v_2) Pr(V=v_2)$
であるから、
　$ Pr(A=a_1 | V=v_1) - Pr(A=a_1) $
　$ = Pr(A=a_1 | V=v_1) (1- Pr(V=v_1)) - Pr(A=a_1 | V=v_2) Pr(V=v_2)$
　$ = (1- Pr(V=v_1)) \{ Pr(A=a_1 | V=v_1) - Pr(A=a_1 | V=v_2) \}$
と書ける。$Pr(V=v_1) < 1$なので(全員が正解に投票するわけではないから)、結局
　$Pr(A=a_1 | V=v_1) - Pr(A=a_1) > 0 \Leftrightarrow Pr(A=a_1 | V=v_1) - Pr(A=a_1 | V=v_2) > 0$
(1)とあわせると
　$Pr(V=v_1 | A=a_1) > Pr(V=v_1|A=a_2) \Leftrightarrow Pr(A=a_1 | V=v_1) > Pr(A=a_1 | V=v_2)$
ということになる。ぜぇぜぇ。これを(2)としよう。

　投票ルールの定義により、所与のシグナル$S=s_k$の下で$V=v_1$である必要十分条件は
　$Pr(A=a_1|S=s_k)/c_1 > Pr(A=a_2|S=s_k))/c_2$
$d=Pr(A=a_1|S=s_k)$と置くと
　$d/c_1 > (1-d)/(1-c_1)$
　$(1-c_1)d > c_1(1-d)$
　$d-c_1d > c_1 - c_1d$
　$d > c_1$
従って、所与のシグナル$S=s_k$の下で
　$V=v_1 \Leftrightarrow Pr(A=a_1|S=s_k) > c_1$
である。同様に、
　$V=v_2 \Leftrightarrow Pr(A=a_1|S=s_k) < c_1$
ということは、任意の$s_k$の下で
　$Pr(A=a_1 | V=v_1) = Pr(A=a_1 | Pr(A=a_1|S=s_k) > c_1) > c_1$
　$Pr(A=a_1 | V=v_2) = Pr(A=a_1 | Pr(A=a_1|S=s_k) < c_1) < c_1$
従って$Pr(A=a_1 | V=v_1) > Pr(A=a_1 | V=v_2)$である。
　これは(2)の右側の条件である。従って、左側の条件
　$Pr(V=v_1 | A=a_1) > Pr(V=v_1|A=a_2)$
も成り立つ... ということだと思う。

A respondent with signal $s_j$ computes excected votes by marginalizing across the two possible worlds, $p(v_{i*}|s_j) = p(v_{i*}|a_{i*}) p(a_{i*}|s_j) + p(v_{i*}|a_k) p(a_k|s_j)$. The actual vote for the correct answer is no less than the counterfactual vote, $p(v_{i*}|a_{i*}) \geq p(v_{i*}|a_k)$.
Therefore, $p(v_{i*}|s_j) \leq p(v_{i*}|a_{i*})$, with strict inequality unless $p(a_{i*}|s_j) = 1$. Because weak inequality holds for all signals, and is strict for some, the average predicted vote will be strictly underestimated. (QED)

　[シグナル$S=s_j$を持つ対象者$r$が計算する他人$q$の投票についての確率$Pr(V^q=v_1|S^r=s_j)$は、世界で場合分けして
　$Pr(V^q=v_1|S^r=s_j) $
　$= Pr(V^q=v_1|A=a_1)Pr(A=a_1|S^r=s_j) + Pr(V^q=v_1|A=a_2)Pr(A=a_2|S^r=s_j)$
式を簡単にするために$c=Pr(A=a_1|S^r=s_j)$と置くと
　$= c Pr(V^q=v_1|A=a_1) + (1-c)Pr(V^q=v_1|A=a_2)$
つまり、他人が$a_1$に投票する確率$Pr(V^q=v_1|S^r=s_j)$は、正解が$a_1$であるときに他人が正解に投票する確率$Pr(V^q=v_1|A=a_1)$と、正解が$a_2$であるときに他人が正解に投票する確率$Pr(V^q=v_1|A=a_2)$のあいだのどこかの値となる。正解が$a_1$である確率$c=Pr(A=a_1|S^r=s_j)$がその位置を決めているわけである。
　さて、この2つの確率について上で苦労して検討した結果、$Pr(V^q=v_1|A=a_1) > Pr(V^q=v_1|A=a_2)$であることがわかっている(原文では$\geq$となっているが、誤植と考え書き換えた)。
　ということは、
　$c=1$のときに$Pr(V^q=v_1|S^r=s_j) = Pr(V^q=v_1|A=a_1)$
　$c < 1$のときに$Pr(V^q=v_1|S^r=s_j) < Pr(V^q=v_1|A=a_1)$
である。$c=Pr(A=a_1|S^r=s_j)$は$s_j$によっては1でありうるが、その場合でも残りの$s_j$については0である。従って、対象者が所与のシグナルの下で計算するところの「他人が正解に投票する確率」$Pr(V^q=v_1|S^r=s_j)$は、対象者を通じて平均すると、実際の「他人が正解に投票する確率」$Pr(V^q=v_1|A=a_1)$より小さくなる。
　すなわち、「みんなが思うよりも意外に多い」回答は正解である。]

　以上、p.5までの内容でありました。先は長い... くじけそう...

雑記：データ解析 - 「みんなが思うよりも意外に多い」回答はなぜ正しいか：その2

　島根と鳥取、西側にあるのはどっちだろうか。あいにく地図が手元になく正解がわからない。そこで、たくさんの人に対してアンケートを行い、その回答の集計から正解を導きたい。
　このとき、多数決はよろしくない。たとえば、西側にあるのはどっちだと思うかと人々に尋ねたところ、島根の得票率が4割、鳥取の得票率が6割となったとしよう。だからといって、鳥取が西側にある、と考えるのはよろしくない。
　人々の知恵をうまく集約するには、むしろ次のように集計するのが良い。人々に2問尋ねる。(1)西側にあるのはどっちか。(2)自分と同じ回答をする人は何割いるか。で、「みんなが思うよりも意外に多い」回答が正解だと考える。
　たとえば、(1)の回答で島根の得票率が4割であったとしよう。かつ、(2)の回答(得票率の予測)を平均すると島根が3割であったとしよう。つまり、「島根が西だ」という回答は全体の3割くらいだろうと人々は思ったが、実際には4割だったわけだ。このとき、「島根が西」説は少数派ではあるけれど、ほんとうは島根が西だと判断すべきだ。

　... というのが、Prelec, Seung, & McCoy (2017, Nature)の主張である。
　わたくし、ここ何年も、足りない頭でこの問題を考え続けているのだが、正直なところ、いまだにキツネにつままれたような思いが消えない。
　なぜ「みんなが思うよりも意外に多い」回答が正解なのか？ 以下ではその徹底的な解説を試みる。
　なお、元ネタは上記論文のSupplementary Information pp.1-8 である。４回にわけてゆっくり読み進めることにする。改めていうまでもないことだが、主たる想定読者は私自身である。

セッティング
　いまここに$m$個の可能世界がある。うちひとつが現実である。私たちはどの世界が現実なのかを知らない。そこで、$m$個の選択肢を提示し、いずれが正しいと思うかを人々に聴取し、その回答から、どの可能世界が現実かを同定したい。

　世界を確率変数$A$で表す[原文にはない記号だが、わかりやすくするために付け加えた]。$A$は$m$個の可能世界$\{a_1, \ldots, a_m\}$を値としてとる。[ここでは、$a_1$を「島根が西にある世界」, $a_2$を「鳥取が西にある世界」としよう]

　対象者$r$が持っている証拠を、プライベートな「シグナル」$S^r$とみなす。対象者間の知識の差異はすべてシグナルで表現されていると考える。$S^r$はカテゴリカル確率変数で、値として$\{s_1, \ldots, s_n\}$をとる。[ここでは、$s_1$を「島根が西だと学校で教わった」, $s_2$を「鳥取が西だと友達に教わった」, $s_3$を「鳥取って西っぽいと思う」としよう。ある人の知識状態はこの3つのうちどれかひとつだ]

　世界$a_i$の下で、異なる対象者のシグナルは独立に確率分布$Pr(S = s_k | A = a_i)$に従うと考える。[原文では$p(s_k | a_i)$と略記されているのだが、理解を確かめるために、以下いちいち確率変数名を補完して書き直す。縦棒左側の$s_k$は、ここでは$r$さんに限らずすべての人に与えられるシグナルを指しているのだと思うので、原文にそんな表記は出てこないけど$S$と書くことにする]

　世界についての事前分布を$Pr(A=a_i)$とする。この事前分布は、すべての回答者の共通知識である証拠と整合的な確率を与えていると考える。[ここでの例でいうと、仮に知識ゼロの状態だったら、島根が西だと思うか鳥取が西だと思うかの信念の程度には個人差がない]

　対象者は同時確率$Pr(S = s_k, A=a_i)$を知っていると想定する($Pr(A=a_i), Pr(S = s_k)$はともに0より大とする)。この同時確率が可能世界モデルを定義している。しかし人々は、どの$a_i$が正解($a_{i*}$)かを知らないし、シグナルの実際の分布も知らない。[すべての対象者は、こころのなかに表1aを持っている。この表自体には個人差はない。でも、人は自分が上の行の地球に生きているのか下の行の地球に生きているのかを知らない。また、この表のほかに、自分が何を知っているかは知っている。でも他の人がどんな知識を持っているかは知らない]

　対象者は２つのタイプの信念を持つ。どちらの信念も、与えられたシグナル$s_k$と、既知の同時確率$Pr(S＝s_k, A=a_i)$から算出される。

  1. 正解についての信念$Pr(A = a_i | S = s_k)$。[表1b]
  2. 他の回答者が受け取っているシグナルについての信念 [表1c]。すなわち、ランダムに選ばれた他の回答者$q$について、
    　$Pr(S^q = s_j | S^r = s_k) = \sum_i Pr(S^q=s_j | A=a_i) Pr(A= a_i | S^r=s_k) $
    [原文では右辺は$\sum_i p(s_j|a_i)p(a_i|s_k)p(a_i)$となっているのだが、最後に$p(a_i)$を掛ける理由がわからない... 大変僭越ながら誤植と捉えて取り除いている]

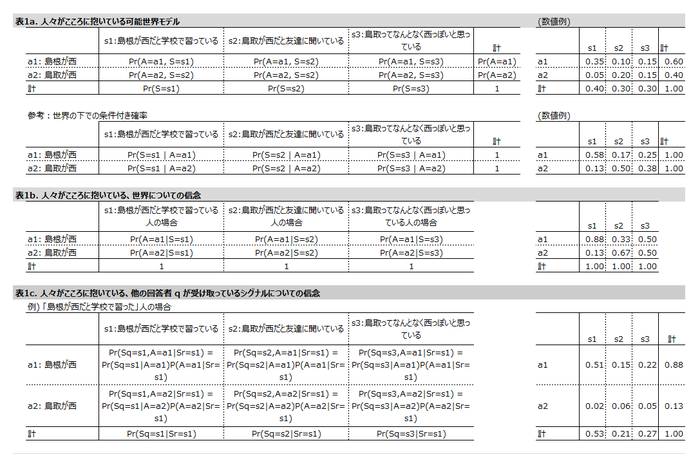
table1.png
定理1
[私の理解では、ここは論文の本筋ではなく、前置きに当たる議論である]

定理1. 実際のシグナルの分布についての知識$Pr(S = s_k | A=a_i*)$と、それらのシグナルによって示唆される事後確率 $Pr(A=a_i | S = s_k)$に依存するアルゴリズムからは、正解は演繹できない。

　証明：
　以下では、これらのシグナル分布と、恣意的に選んだ答えについての事後確率を生成するような、ある可能世界モデルを構築することを試みる。

　正解$a_{i*}$は未知、でもシグナルの分布 $Pr(S=s_k | A=a_{i*})$は既知だとしよう。また事後確率$Pr(A=a_j | S=s_k)$も既知だとしよう。[シグナルの分布を表2に示す。なお、本文で$a$の添え字が$i$じゃなくて$j$になっているのは、次の段落から$a_i$を「選択した任意の答え」という意味で用いるからではないかと思う]table2.png

　任意の$a_i$を選び、それに対応する可能世界モデル$q(S=s_k, A=a_j)$を構築する。このモデルは、 $i*=i$であるときの既知のシグナル分布と事後確率を生成するものである。 [つまり、これから試したいことは、表1と表2から、表3を決めることだ。もし＜島根が西バージョン＞と＜鳥取が西バージョン＞の両方が作れたら、それは困ったことになる] 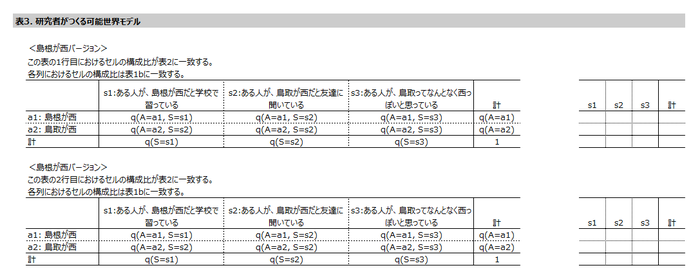table3.png　既知のパラメータはシグナルを通じた事前分布を制約していない。そこで次のように設定しよう。
　$\displaystyle q(S=s_k) = \frac{Pr(S=s_k | A=a_{i*})}{Pr(A=a_i | S=s_k)} \left( \sum_j \frac{Pr(S=s_j | A=a_{i*})}{Pr(A=a_i | S=s_j)} \right)^{-1}$
　[第2項は$q(S=s_k)$の$k$を通じた和を1にするための規準化項。第1項の分子は表2。分母は、表1bにおけるいま選んでいる世界$a_i$の確率。なぜこう設定するのか理解できていないのだが、ここは「もし表3の列和をこう設定したら」という話がしたいだけで、意味を考えずに先に進んで良いところなのかも??? ともあれ、いま表3は下表のとおり]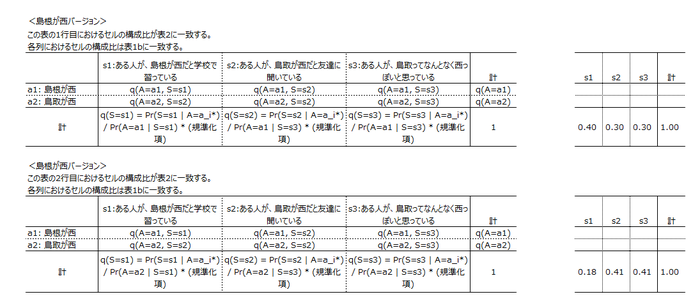table3_1.png　可能世界モデルから生成される事後確率は既知の事後確率と一致していないといけない。すなわち、全ての$k, j$について、
　$q(A=a_j | S=s_k) = p(A=a_j | S=s_k)$
が成り立たなければならない。[表3の各列内のセル構成比が、表1bに一致していないといけない]

　以上を踏まえると、可能世界モデルが次のように固定される。
　$q(A=a_j, S=s_k) = q(A=a_j | S=s_k) q(S=s_k)$

　この同時分布から、回答を通じた事前分布を求めることができる。まず
　$q(A=a_i, S=s_k)$
　$= q(A=a_i | S=s_k) q(S=s_k)$
さきほど設定した$q(S=s_k)$を代入すると、$q(A=a_i|S=s_k)=p(A=a_i|S=s_k)$が消えて
　$\displaystyle = p(S=s_k | A=a_{i*}) \left( \sum_j \frac{p(S=s_j | A=a_{i*})}{p(A=a_i | S=s_j)} \right)^{-1}$
シグナルを通して合計すると
　$\displaystyle q(A=a_i) = \left( \sum_j \frac{p(S=s_j | A=a_{i*}}{p(A=a_i | S=s_j)} \right)^{-1}$
　こうして、可能世界モデルの周辺分布$q(S=s_k), q(A=a_i)$が手に入った。

　さて、周辺分布$q(S=s_k), q(A=a_i)$、事後分布$q(a_j|s_k)=p(a_j|s_k), k=1, \ldots, n$からつぎのことがわかる。正解が$a_i$であるとき、観察されるシグナルの分布
　$\displaystyle q(S=s_k | A=a_i) = \frac{q(A=a_i | S=s_k) q(S=s_k)}{q(A=a_i)}$
に、周辺分布$q(S=s_k), q(A=a_i)$を代入すると
　$=p(S=s_k | A=a_{i*})$
となる。つまり、どんな$a_i$を選んでも、既知の事後分布を生成できる。証明終。
　[このくだりの理路にはいまいちついていけないんだけど、こういうことじゃないかと思う。もし「島根が西」だといいたければ下表の上のような可能世界モデルを考えることができるし、「鳥取が西」だといいたければ下のような可能世界モデルを考えればよい。どちらも、表1と表2に対してつじつまが合う。いいかえると、表1と表2が決まっても、表3は決められない。]table3_2.png　[いまこの地球上において、 「島根が西だと学校で教わった」 「鳥取が西だと友達に教わった」 「鳥取って西っぽいと思う」 のそれぞれの知識を持つ人が占める割合$Pr(S = s_k | A=a_i*)$、すなわち表2が、どうやって調べるのかわかんないけど、とにかくなんらかのすごい方法でわかったとしよう。また、島根が西である時になにが起きるか、鳥取が西である時に何が起きるかについて人々は知っており(表1)、それもなんらかのすごい方法でわかったとしよう。研究者はこの2つの表を組み合わせて、島根が西なのか鳥取が西なのかを知ることができるだろうか？
　一見できそうなものだが、実は無理なのだ、だから、たとえば回答とともにその確信度を聴取してみたりして、人々の知識をいくら正確に調べようとしたところで、世界がどうなっているのかは結局わからないんだよ。というのが、この定理がいわんとしていることなのだと思う]

　これでようやくp.4の半ば。先は長いぞ。

雑記：データ解析 - 「みんなが思うよりも意外に多い」回答はなぜ正しいか：その1

この春から、誰ともろくに喋らずネットにもアクセスせず、静かに暮らす日々が続いていたもので、読んだ資料のメモもそれなりに溜まってきた。せっかくなので順次載せていくことにしよう。

Prelec, D., Seung, H.S., & McCoy, J. (2017) A solution to the single-question crows wisdom problem. Nature, 541, 532-535.
　ベイジアン自白剤というわけのわからない話によって哀れな私を翻弄した、Prelecさんの新論文。入手方法がなくて嘆いていたら、M先生が親切にもお送りくださった。ありがとうございますーー、とお勤め先の方角に向かって平伏。

　原稿の準備のために頑張って読んでいたら、逐語訳に近いメモとなってしまった。

　群衆の知恵がいかなる個人よりも優れているという考え方は、かつては物議をかもしたものだが(Goltonをみよ)、いまではそれ自体が群衆の知恵の一部となった。いずれはオンライン投票が信頼される専門家たちを駆逐するかも、などと考える人もいるほどだ(キャス・サンスティーンやスロウィッキーをみよ)。
　群衆から知恵を抽出するアルゴリズムは、たいてい民主的投票手続きに基づいており、個人の判断の独立性を保存する(Lorenz et al., 2011 PNAS)。しかし、民主的手法は低レベルな共通情報に偏りがちだ(Chen et al, 2004 MgmtSci.; Simmons et al., 2011 JCR)。確信度を測って調整する方法もあるけどうまくいかない(Hertwig, 2012 Sci.)。
　そこで代替案をご提案しよう。「もっとも一般的な答え」「もっとも信頼できる答え」ではなく、「人が予測するより一般的な答え」を選ぶのだ。この方法は、機械学習から心理測定まで幅広い分野に適用できる。

　フィラデルフィアはペンシルバニア州の州都でしょうか？ コロンビアはサウス・カロライナ州の州都でしょうか？ 多くの人がyes, yesと答えてしまう(正解はno, yes。ペンシルバニア州の州都はハリスバーグ)。確信度で重みづけて集計しても正解は得られない。
　さて、我々の提案手法はこうだ。対象者に、「この問いに他の人々がどう答えるか」の分布を予測してもらう。で、予測よりも多くの支持を集めた答えを選ぶ。
　このアルゴリズムの背後にある考え方を直観的に示すと次の通り。いま、ふたつの可能な世界、すなわち現実世界と反事実世界があるとしよう。現実世界ではフィラデルフィアは州都でない。反事実世界ではフィラデルフィアは州都だ。現実世界においてyesと答える人は、反事実世界においてyesと答える人よりも少ないだろう。これを歪んだコインのトスをつかって形式化しよう。いまあるコインがあって、現実世界では60%の確率でオモテとなり、反事実世界では90%の確率でオモテとなる。さて、多数派の意見はどちらもyesを支持する。人々はコインが歪んでいることを知っているが、どちらの世界が正しい世界かは知らない。その結果、yes投票率についての人々の予測は60%と90%の間になる。しかるに、現実のyes投票率は60%である。従って、noが「意外に一般的な答え」、すなわち正解となる。[←はっはっはー。2004年のScience論文と比べると格段にわかりやすい説明となっているが、それでもキツネにつままれたような気がしますね]
　この選択原理を「意外に一般的」アルゴリズム(SPアルゴリズム)と呼ぶことにしよう。詳細はSupplementを読め。
　実際に試してみると、フィラデルフィア問題では、yesと答えた人のほぼ全員が「みんなもyesと答えるだろう」と予測し、noと答えた人の多くは「noと答えるのは少数派だろう」と予測した。よって、yes回答は実際よりも高めに予測され、「意外に一般的」回答はnoとなった。いっぽうコロンビア問題では、yes回答率は実際よりも低めに予測された。ね？ 「意外に一般的」回答が正解になっているでしょ？

　対象者の確信度を使って、これと同じくらい妥当なアルゴリズムを構築できるだろうか？
　いま、対象者が世界の事前確率とコインのバイアスを知っているとしよう。さらに、個々の対象者は自分のプライベートなコイン・トスを観察し、ベイズ規則を用いて確信度を算出するとしよう。確信度を使ったアルゴリズムがあるとしたら、それは報告された確信度の大きな標本から実際のコインを同定しなければならない。
　しかし、確信度の分布は同じだが正解が異なる2つの問題の例を示すことができる[と架空例を示しているが、ややこしいので省略]。この例は確信度を使ったアルゴリズムを作れるという主張に対する反例となっている。もちろん、現実の人々は理想化されたベイジアン・モデルに従うわけではないが、ここでいいたいのは、事前確率に基づく手法は理想的対象者においてさえうまくいかないということであって、現実の対象者においてはさらにうまくいかないだろう。
　それに引き替え、SPアルゴリズムは理論的に保障されている。それは利用可能な証拠の下での最良の解だ。さらに、このアルゴリズムは多肢選択設問に拡張できる。また、投票予測によって、正解にもっとも高い確率を与えている対象者を同定できる。これらの結果は、歪んているコインの例を多面コインへと一般化する理論に基づいている。

　[ここで4つの実験を駆け足で紹介。正解がわかっている設問について、多数の支持を得た選択肢、SP、確信度で重みづけた集計での一位選択肢、確信度最大の選択肢、を比較する。どの設問でも、正解との相関はSPが一番高い]。

　SPの成績は、対象者が利用できる情報、そして対象者の能力によって、常に制約されるだろう。利用可能な証拠が不完全ないしミスリーディングであれば、その証拠にもっともフィットする答えは不正解となるだろう。この限定は、設問を注意深く言い換えることでよりはっきりさせることができる。たとえば、「世界の気温は5%以上上がるでしょうか」という設問は「世界の気温は5%以上上昇するかしないか、 現在の証拠に照らしてどちらがありそうでしょうか」と言い換えることができる。
　SPアルゴリズムは、理想的回答からのいくつかの逸脱に対して頑健である(Supplementをみよ)。たとえば、もし対象者が両方の世界について考えその中間の予測を行うのではなく、自分が正しいと信じる世界の投票率だけを予測したとしても、SPの結果は変わらない。また、対象者にとって予測課題が難しすぎると感じられ、50:50と予測したりランダムな予測値を出したりした場合、SPの結果は多数派の意見に接近するが、方向としては正しいままである。
　政治や環境問題の予測のような論争的なトピックにこの手法を適用する際は、操作を防ぐことがじゅゆ用になる。たとえば、対象者は不誠実に低い予測を示して、特定の選択肢を勝たせようとするかもしれない。こうした行動を防ぐためには、ベイジアン自白剤で真実申告にインセンティブを与えることができる。Prelec(2004 Sci.), John, Lowenstein, & Prelec(2012 Psych.Sci.)をみよ、我々はすでに「意外に一般的」原理が真実の診断に使えることを示している。
　予測市場とのちがいについて。SPは検証不可能な命題についても使えるところが異なる。

　意見集約においてはこれまで民主的手法の影響力が強く、また生産的でもあったのだが、それらの手法はある意味で集合知を過小評価するものであった。人々は自分の実際の信念を述べるように制約されていた。しかし、人々は仮説的シナリオの下でどんな信念が生じるかを推論することもできる。こうした知識を用いれば、伝統的な投票がうまくいかないときにも真実を復元できる。もし対象者が、正解を構築するに十分な証拠を持っていれば、「意外に一般的」原理はその答えをもたらす。より一般的にいえば、「意外に一般的」原理は利用可能な証拠の下での最良の答えをもたらす。
　これらの主張は理論的なものである。実際の対象者は理想と違うから、現実場面での成功は保障されない。しかし、ペンシルバニア問題のような単純な問題で、理想的対象者においてさえ失敗するような手法を信頼するのは難しい。我々の知る限り、提案手法はこのテストを通過する唯一の手法である。

　... 「意外に一般的」原理はベイジアン自白剤(2004年のScience論文)の基盤でもあったので、理論的に新しい展開というわけではないんじゃないかしらん？
　いっぽう論文のストーリーは2004年の論文と大きく異なり、「意外に一般的」原理をスコアリング・ルールの基盤としてではなく、単なる意見集約アルゴリズムとして説明している。

論文：予測市場 - 読了：Prelec, Seung, & McCoy (2017) 「みんなが思うよりも意外に多い」回答が正解だ

« 2017年3月 | メイン | 2017年9月 »

rebuilt: 2020年11月16日 22:39
validate this page