elsur.jpn.org >

« 2018年6月 | メイン | 2018年8月 »

2018年7月31日 (火)

Powers, D. (2018) Thinking in trends: The rise of trend forecasting in the United States. Journal of Historical Research in Marketing, 10(1), 2-20.
　ちょっと用事があって手に取ったやつ。アメリカのトレンド予測企業BrainReserveの創立者にして、アメリカのお茶の間でも知られているという有名人Faith Popcornさんを中心に、70-90年代の米トレンド予測産業の勃興と繁栄を振り返るというマーケティング史の論文。研究としての価値は全然分かんないんだけど、面白く読んだ。

　アメリカでトレンド予測が産業として成立したのは70年代初頭なのだそうだ。アルビン・トフラーの本がベストセラーになり、人々が未来の不透明さに対する恐怖に突き落とされた時代である。当時の主要な未来予測手法はシナリオプランニングとデルファイ法。いずれもマクロレベルの要因に焦点を当てていた。いっぽうマーケターたちは、消費者のなかのイノベーターやアーリー・アダプターに注目しはじめた。ところが現実には、誰がイノベーターやアーリー・アダプタ―なのかを決めるのは難しい。というわけで、いま起きている文化的現象をわかりやすく翻訳してくれる専門家が求められるようになり、Feith Popcornをはじめとしたトレンド予測家たちや各種サービスが繁栄を謳歌する時代がやってくる...

　いまとなっては、Popcornがある種の予言者だったのか、それともただの商売人だったのかはあまり大した問題ではない。むしろ重要なのは、彼女とその仲間たちの成功が、文化予測の役割と影響についてなにを語っているかである。70年代、トレンド予測は未来という脅威を未来という好機へと変換した。まず企業と文化の間の壁を打ち壊すことによって、次に文化の未来を覗き見る小窓としての「トレンド」を提供することによって。20年後、ニューズウィーク誌はこの数十年間でもっともホットであった職業のひとつとしてトレンド予測を挙げたが、それはもはや一般化しすぎてしまい、縮小を余儀なくされているとも示唆している。いまや、冷酷なまでの変動がアメリカ人の生活における標準となり、ビジネスの基本要素となった。未来を予測するという行為は、この不安定性を和らげることを意図していたのだが、実際には、未来をひとくくりにして名前を付け文化へと送り返すことによって、むしろ不安定性を加速する役割を果たした。[...]トレンド予測家の未来論について考えるとき、正しいか正しくないかは良い物差しではない。トレンド予測家たちは文化を分析し、世界がそれに乗って進んでいくと想定されているトレンドへと変換した。それは未来の予測でもなければ未来のでっちあげでもなかった。彼らは未来を生み出していたのである。

　...なるほどねえ。トレンド予測には予言の自己成就のような側面があったわけね。
　存じ上げなかったんだけど、Faith Popcornさんは御年71歳。たくさんの流行語を世に送り出したマーケター・著述家らしい。いまの日本で言うとどういう人なんですかね。三浦展さんとか？

論文：マーケティング - 読了：Powers (2018) トレンド予測産業とその時代

2018年7月30日 (月)

Wakimoto (1971) Stratified random sampling (I) Estimation of the population variance. Annals of the Institute of Statistical Mathematics, 23(1), 233–252.
Wakimoto (1971) Stratified random sampling (II) Estimation of the population covariance. Annals of the Institute of Statistical Mathematics, 23(1), 327-337.
Wakimoto (1971) Stratified random sampling (III) Estimation of the correlation coefficient. Annals of the Institute of Statistical Mathematics, 23(1), 339-353.

　層別抽出デザインにおける母分散・母共分散・母相関の推定について述べた3本の論文。仕事の都合で読んだ。
　複雑な標本抽出デザインにおける推定量の分散について解説している資料は多いけど、母分散の推定について述べているものが全然見当たらず(探し方が悪いのかもしれないけど)、思い余って1971年の論文をめくった次第である。掲載誌は日本の統計数理研究所が出している英文誌。著者の脇本さんという方は昭和40年代に統数研に勤めていた方で、その後郷里の岡山大に移り、平成5年に亡くなった由。
　
　読んだというよりもめくったというのが正しいのだが、まあとにかく、だいたいどんなことが書いてあったかをメモしておく。

(I) 母分散の推定

　$X$の分布関数を$F(x)$とする。層の数を$L$とし、$i$番目の層の分布関数を$F_i(x)$とする。層の割合を$w_i$とする($\sum_i^L w_i = 1$)。

　定理1. $X_{i1}, \ldots, X_{in_i}$が$F_i(x)$にiidに従い、どの$i$についても$n_i \geq 2$であるとき、母分散$\sigma^2$の不偏推定量は
　$ U_{s,n}$
　$\displaystyle = \sum_i \frac{w^2}{n_i (n_i)} \sum_{k < l}^{n_i} (X_{ik}-X_{il})^2$
　$\displaystyle + \sum_{i < j}^L \frac{w_i w_j}{n_i n_j} \sum_k^{n_i} \sum_l^{n_j} (X_{ik} - X_{jl})^2$
　[なぜか最初からペアの差によって定義してあるので途方にくれたが、平均からの偏差によって定義すると、これは
　$\displaystyle U_{s,n} = \sum_i w_i U_i + \sum_i w_i (\bar{X}_i - \bar{X}_n)^2 - \sum_i \frac{w_i(1-w_i)}{n_i} U_i$
　となるそうだ。ただし$U_i$ってのは各層における不偏分散, $\bar{x}_n = \sum_i w_i \bar{X}_i$。第1項は層内分散、第2項は層別の標本平均を使って求めた層間分散、第3項は層間分散が標本平均を使っちゃっていることによるバイアスを補正する項なのだろうと思う]

　定理2. $U_{s,n}$の分散$V(U_{s,n})$は...[略]

　$U_{s,n}$の漸近正規性について... [難しくてよくわからん]

　$n_i = w_i n$とする場合を代表サンプリングないしBowleyサンプリングと呼び、標本サイズのことを「比例割当」と呼ぶ。このとき、母分散推定量$U_{s,p,n}$と$V(U_{s,p,n})$は...[略]
　いっぽう、単純無作為抽出のときの母分散推定量$U_{r,n}$と$V(U_{r,n})$は...[略]

　定理3. $V(U_{r,n}) - V(U_{s,p,n})$は...[略]

　というわけで、$n$が大きければ$V(U_{s,p,n})$は$V(U_{r,n})$より小さい。[←よく母平均推定において層別抽出は単純無作為抽出より有利だというけれど、母分散推定という観点から見ても、比例層別抽出は単純無作為抽出よか有利だってことね]
　いっぽう、層別をしくじったケースでは逆転することもある。たとえば$F_1(x) = F_2(x) = \cdots = F_L(x)$のときとか。[←なるほど...層別するからには層間で分布がちがわないといかんということね]

　$V(V_{s,n})$を最小化するように$n_i$を決めるという最適割当について考えると... [この節まるごとパスするけど、専門家というのはいろんなことを考えるものだなあ。なお、イントロにある要約によれば、理論上は最適割当を考えることはできるけど、そのために必要な事前情報がふつう手に入らないので、実務的には比例割当がお勧めである由。はっはっは]

　比例割当の場合の最適層別について... [まじか、母分散推定のために層別を最適化するなんていう発想もあるのか。ひょえー。パス]

(II) 母共分散の推定

　$X, Y$の同時分布関数を$F(x,y)$とする。母平均を$\mu_x, \mu_y$, 分散と共分散を$\sigma_{xx}, \sigma_{yy}, \sigma_{xy}$とする[←論文(I)とちがって二乗の添字がついてない。面倒くさくなったのかな？]。層の数を$L$とし、$i$番目の層の同時分布関数を$F_i(x,y)$とする。

　定理1. $(X_{i1}, Y_{i1}), \ldots, (X_{in_i}, Y_{in_i})$が$F_i(x,y)$にiidに従い、どの$i$についても$n_i \geq 2$であるとき、母共分散$\sigma_{xy}$の不偏推定量は
　$\displaystyle U_s$
　$\displaystyle = \sum_i \frac{w^2}{n_i(n_i-1)} \sum_{k < l}(X_{ik}-X_{il})(Y_{ik}-Y_{il})$
　$\displaystyle + \sum_{i < j}\frac{w_i w_j}{n_i n_j} \sum_k^{n_i} \sum_l^{n_j} (X_{ik} - X_{jl})(Y_{ik} - Y_{jl})$
　[ここでもいきなりペアの差で定義してあるので面食らうわけですが、第1項は層内共分散、第2項は層間共分散なのでありましょう]

　定理2. $U_s$の分散$V(U_s)$は...[略]

　$U_{s}$の漸近正規性について... [難しくてよくわからん]
　推定量の精度は層別無作為抽出のせいでどのくらい改善するかというと...[パス]
　最適割当は...[パス]
　比例割当の場合の最適な層別は...[パス]

(III) 相関係数の推定

　母相関係数を$\rho_{xy}$とする。

　[まず$\sigma_{xx}, \sigma_{yy}, \sigma_{xy}$の推定量とその分散についておさらいがあって...]
　$\rho_{xy}$の推定量を以下とする。
　$R_s = U_{s,xy} (U_{s,xx} U_{s,yy})^{-1}$
　[手元のPDFだと字がかすれちゃってよくわからないんだけど、たぶん上の式であっていると思う。えーと、ちょっと待って、これって一致推定量ではあるけど不偏じゃないと思うんですけど、あってますかね？]

　定理1. $|E[R_s - \rho_{xy}]|$の上界は...[省略するけど、すっごくややこしい式になる。3頁にわたる証明がついている。思うに、ここが3本の論文を通じたハイライトシーンなんだろうな]

　定理2. $R$のMSE $E[(R_s -\rho_{xy})^2]$は...[省略。この式だけで1ページくらい占めている。すげえなあ]

　推定量の精度は層別無作為抽出のせいでどのくらい改善するかというと...[パス]
　比例割当の場合の最適な層別は...[パス]

論文：データ解析(2018-) - 読了：Wakimoto (1971) 層別抽出デザインにおける母分散・母共分散・母相関の推定

2018年7月29日 (日)

　仕事の関連でお問い合わせ頂いて、いちおうお返事はしたんだけど、その途中で、よくよく考えてみたらこれって不思議だなあ、ということがでてきた。

　層別抽出標本から母分散を推定するという問題について考える。標本推定量の分散の推定じゃなくて母分散そのものの推定である。こういう話、本にはなかなか載ってない。そりゃそうかもな、そんな用事はあんまりないような気もする。

　層$h (=1,\ldots, H)$の$i(=1,\ldots,n_h)$個目の値を$x_{hi}$とし、層が母集団に占める割合を$P_h$とする。すべての層を通じた標本サイズを$n = \sum_h^H n_h$とする。
　層ごとの平均は $\bar{x}_h = (1/n_h) \sum_{i}^{n_h} x_{hi}$
　全体平均は $\bar{x}_{Total} = \sum_h^H P_h \bar{x}_h$
　層ごとの分散は $S^2_h = (1/n_h) \sum{i}^{n_h} (x_{hi}-\bar{x}_h)^2$
　層内分散は $S^2_{Within} = \sum_h^H P_h S^2_h$
　層間分散は $S^2_{Between} = \sum_h^H P_h (\bar{x}_h - \bar{x}_{Total})^2$
　全分散は層内分散と層間分散の和だから、$S^2_{Total} = S^2_{Within} + S^2_{Between}$が答えだ。と思いません？？

　例を挙げて計算してみよう。層1の値が$(1,2,3)$, 層2の値が$(1,2,3,4,5,6,7)$、どちらの層も母集団に占める割合は$1/2$とする。
　層ごとの平均は$\bar{x}_1 = 2, \bar{x}_2 = 4$
　全体平均は$\bar{x}_{Total} = 3$
　層ごとの分散は $S^2_1 = 0.667, S^2_2 = 4$
　層内分散は $S^2_{Within} = 2.333$
　層間分散は $S^2_{Between} = 1$
　全分散は $S^2_{Total} = S^2_{Within} + S^2_{Between} = 3.333$
となる。なりますよね？
　
　とここまで考えて、あれれ？おかしいな？と気が付いた次第である。
　だって、母分散を推定したいわけでしょ？ 不偏推定したいでしょ？ だったら、層ごとの分散の分母は$n_h$じゃなくて$n_h-1$じゃない？つまり、層ごとの分散は
　$U^2_h = (1/(n_h-1)) \sum_i^{n_h} (x_{hi}-\bar{x}_h)^2$
じゃない？
　こうして求める全分散を$U^2_{Total,1}$と呼ぼう。実例で計算し直すと
　層ごとの分散は $U^2_1 = 1, U^2_2 = 4.667$
　層内分散は $U^2_{Within} = 2.833$
　全分散は $U^{2}_{Total,1} = U^2_{Within} + S^2_{Between} = 3.833$
となる。

　とここまで考えて、さらに、あれれ？さらにおかしいな？と気がついたわけである。
　層ごとの分散$S^2_h$を標本分散から不偏分散に代えたのに、層間の分散$S^2_{Between}$はそのままでよろしいわけ？
　散々探してついに見つけたのだが、よろしくないらしい。Wakimoto(1971)によれば、母分散の不偏推定量は
　$U^2_{Total} = U^2_{Within} + S^2_{Between} - \sum_h^H P_h(1-P_h) U^2_h/n_h$
なのだそうである(p.235, 記号は原文から書き換えました)。$S^2_{Between}$はちょっと大きめになってしまうので第3項を引く、っていうことなんじゃないかと思う。
　これを$U^2_{Total,2}$と呼ぼう。実例で計算し直すと、
　層間分散は $U^2_{Between} = 1 - 0.25 = 0.75$
　全分散は $U^2_{Total,2} = U^2_{Within} + U^2_{Between} = 3.583$
となる。

　ところで... 四の五の言わずに、上記の$S^2_{Total}$を$n/(n-1)$倍すればいい、という考え方もあるかもしれない。
　この考え方は次のように言い換えることもできる。母分散ってのは値と母平均との差の二乗の母平均のことであり、不偏分散ってのは値と標本平均の差の二乗の合計を(標本サイズ-1)で割った値のことだ。だから、まず全体平均$\bar{x}_{Total}$を求め(もちろん単純な平均ではなく、層ごとの平均を$P_h$で重みづけて合計する)、次に標本のそれぞれの値から$z_{hi} = (x_{hi} - \bar{x}_{Total})^2$を求め、その合計を求め(各層の合計を$P_h$で重みづけて合計する)、最後に$n-1$で割ればよい。
　あるいは、こういう風に考えることもできる。複雑な抽出デザインのデータを分析する際によく行われているように、それぞれの値に確率ウェイトを付与しよう。層別抽出の場合、確率ウェイトとは、各層における標本抽出確率(母集団のある層に属しているある個体が、標本として選ばれる確率)の逆数に比例した値である。このデータの場合、層1では5/3=1.667, 層2では5/7=0.714を与えればよい。さて、このデータが層別抽出であることを無視し、データ$x_1, \ldots, x_n$にウェイト$w_1, \ldots, w_n$が付与されているのだと考える。このウェイトを頻度ウェイト、すなわち「標本におけるその行の出現頻度」として捉えてしまい、不偏分散
　$\sum_i^n w_i (x_i - \bar{x}_{Total})^2 / (\sum_i^n w_i - 1)$
をしれっと求める。
　これを$U^2_{Total, 3}$と呼ぼう。実例で計算すると、
　全分散は $U^2_{Total, 3} = S^2_{Total} * n / (n-1) = 3.333 * 10 / 9 = 3.704$

　では統計ソフトでやってみよう。Mplus, SAS, Rで試す。

　Mplusの場合、次のようなコードで試してみたところ

DATA:

  FILE IS data.dat;

VARIABLE:

  NAMES ARE X nStrata gWeight; 

  WEIGHT = gWeight;

  STRATIFICATION = nStrata; 

ANALYSIS:

  TYPE = COMPLEX;

　分散は3.333と推定された。すなわち$S^2_{Total}$である。
　これはまあ、わかる。標本分散は母分散の不偏推定量ではないが、正規分布に従う変数については、母分散の最尤推定量である。MplusはXの正規性を仮定し、最尤推定値を返しているわけだ。これはMplusのポリシーなので、そうですか、としかいいようがない。

　SASの場合、層別抽出で得た平均の分散を求めることは簡単なんだけど(PROC SURVEYMEANS)、母分散はすぐには推定できそうにない。散々探した末、ようやくSAS社による解説を発見した。
　サンプルコードを書き換えたコードがこちら。SAS University Editionで試しました。

dm log 'log; clear' ; dm output 'output; clear'; 

data ttt; 

  input strata value; 

  datalines;

1 1

1 2

1 3

2 1

2 2

2 3

2 4

2 5

2 6

2 7

;

run;

data ttt; 

  set ttt; 

  if strata = 1 then weight = 5/3; 

  if strata = 2 then weight = 5/7; 

run;

proc surveymeans data = ttt mean stacking  ; 

  stratum strata ; 

  var value; 

  weight weight; 

  ods output Statistics = Statistics Summary = Summary;

run; 

data _null_;

   set Statistics;

   call symput("Mean", Value_Mean);

run;

data Summary;

   set Summary;

   if Label1="重みの合計" then call symput("N",cValue1);

run;

%put _user_;

data Working;

   set ttt;

   z=(1/(&N-1))*(value-&Mean)**2;

run;

proc surveymeans data = Working sum stacking;

   weight weight;

   var z;

run;

　結果は3.704、つまり$U^2_{Total, 3}$である。あっれえええ？
　コードを読むとわかるのだが、ここでやっているのは、「$z_{hi} = (x_{hi} - \bar{x}_{Total})^2$の合計を$n-1$で割る」という、まさに$U^2_{Total, 3}$の考え方に従った処理なのである。

　Rの場合、複雑な抽出デザインの分析はsurveyパッケージが定番である。母分散を推定する関数はsvrvar()である。次のコードで試してみたところ

dfData <- data.frame(

  X = c(1,2,3,1,2,3,4,5,6,7),

  nStrata = c(rep(1, 3), rep(2, 7)),

  gWeight = c(rep(5/3, 3), rep(5/7, 7))

)

oDesign <- svydesign(

  ids    = ~ 0, 

  strata = ~nStrata, 

  weight = ~gWeight,

  data   = dfData

)

print(svyvar(~ X , data=dfData, design=oDesign, estimate.only =TRUE))

　分散は3.704と推定された。あっれえええ？
　svyvar()のコードをちょっと眺めてみたんだけど、やはり$U^2_{Total, 3}$のような処理をやっている模様である。

　というわけで、SAS社のお勧めの方法でも、Rのsurvey::svyvar()でも、母分散の推定量は$U^2_{Total, 3}$となっていることがわかった。
　私、正直、納得いかないです... 正しい推定量は$U^2_{Total, 2} $なのではなかろうか？

　毒を喰らわば皿まで、ということで、シミュレーションしてみた。
　層は2つとする。変数$X$は、層1においては$N(0,1)$に、層2においては$N(2,1)$に従うとする。層内分散は$1$、層間分散は$1$、よって母分散は$2$である。
　ここからサイズ100の標本を層別抽出し、母分散を推定する。標本における層1のサイズは(10,20,30,40,50)の5水準とし、各水準につき50000回繰り返した。
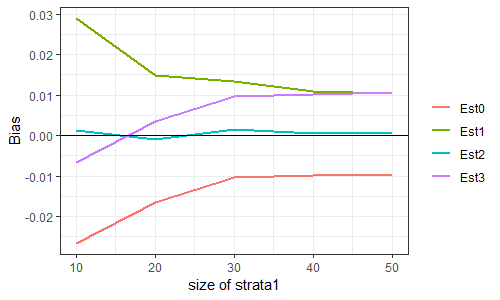
　50000個の母分散推定値の平均から2を引いた値をBiasと呼ぶことにする。これが0に近い推定量が、(不偏性という意味で)良い推定量である。
　推定量は、上記の$S^2_{Total}, U^2_{Total,1}, U^2_{Total,2}, U^2_{Total,3}$の4種類。順にEst0, Est1, Est2, Est3と呼ぶことにする。SAS社の解説やRのsurveyパッケージの出力はEst3である。私が申し上げたいのは、Est2を出力してくれたらいいのになあ、Est3にはバイアスがあるのになあ、ということであります。
　コードと結果はこちら。

library(MASS)

library(dplyr)

library(tidyr)

library(ggplot2)



# - - - - - -

nTOTALSIZE <- 100

anSIZE1    <- seq(10,50,10)

nNUMITER   <- 50000

agMU       <- c(0, 2)

agSIGMASQ  <- c(1, 1)

agPROP     <- c(1/2, 1/2)

# - - - - - -



set.seed(123)

sub_EstimateVar <- function(dfIn){

  anSize        <- tapply(dfIn$X, dfIn$nStrata, length)

  agMean        <- tapply(dfIn$X, dfIn$nStrata, mean)

  agUnbiasedVar <- tapply(dfIn$X, dfIn$nStrata, var)

  agSampleVar   <- agUnbiasedVar * (anSize - 1) / anSize

  agProp        <- tapply(dfIn$gWeight, dfIn$nStrata, sum) / sum(dfIn$gWeight)

  gTotalMean    <- sum(agProp * agMean)

  agBetweenVar  <- sum(agProp * (agMean - gTotalMean)^2)

  gEst0 <- sum(agProp * agSampleVar) +agBetweenVar 

  gEst1 <- sum(agProp * agUnbiasedVar) +agBetweenVar

  gEst2 <- sum(agProp * agUnbiasedVar) + agBetweenVar - sum(agProp * (1-agProp) * agUnbiasedVar / anSize)

  gEst3 <- gEst0 * sum(anSize) / (sum(anSize) -1)

  out <- data.frame(

    gEst0 = gEst0,

    gEst1 = gEst1,

    gEst2 = gEst2,

    gEst3 = gEst3

  )

}

# dfData <- data.frame(

#   X = c(1,2,3,1,2,3,4,5,6,7),

#   nStrata = c(rep(1, 3), rep(2, 7)),

#   gWeight = c(rep(5/3, 3), rep(5/7, 7))

# )

# print(sub_EstimateVar(dfData))



lOut <- lapply(

  anSIZE1, 

  function(nSize1){

    lOut <- lapply(

      1:nNUMITER, 

      function(nIter){

        nSize2 = nTOTALSIZE - nSize1

        data.frame(

          nSize1 = nSize1, 

          nIter  = nIter, 

          X = c(

            rnorm(nSize1, agMU[1], agSIGMASQ[1]),

            rnorm(nSize2, agMU[2], agSIGMASQ[2])

          ), 

          nStrata = c(rep(1, nSize1), rep(2, nSize2)), 

          gWeight = c(

            rep(agPROP[1]/(nSize1/nTOTALSIZE), nSize1), 

            rep(agPROP[2]/(nSize2/nTOTALSIZE), nSize2)

          )

        )

      }

    )

    bind_rows(lOut)

  }

)

dfIn <- bind_rows(lOut)



out <- dfIn %>%

  group_by(nSize1, nIter) %>%

  dplyr::do(sub_EstimateVar(.)) %>%

  ungroup() %>%

  group_by(nSize1) %>%

  summarize(

    Bias_Est0 = mean(gEst0) - 2,

    Bias_Est1 = mean(gEst1) - 2,

    Bias_Est2 = mean(gEst2) - 2,

    Bias_Est3 = mean(gEst3) - 2,

    RMSE_Est0  = sqrt(mean((gEst0 - 2)^2)),

    RMSE_Est1  = sqrt(mean((gEst1 - 2)^2)),

    RMSE_Est2  = sqrt(mean((gEst2 - 2)^2)),

    RMSE_Est3  = sqrt(mean((gEst3 - 2)^2))

  ) %>%

  ungroup()



dfPlot <- out %>%

  gather(sVar, gValue, -nSize1) %>%

  separate(sVar, c("sVar1", "sVar2")) %>%

  filter(sVar1 == "Bias")

g <- ggplot(data=dfPlot, aes(x = nSize1, y = gValue, group=sVar2, color=sVar2))

g <- g + geom_path(size=1)

# g <- g + facet_grid(. ~ sVar1)

g <- g + geom_abline(slope=0, intercept=0)

g <- g + labs(x = "size of strata1", y = "Bias")

g <- g + scale_color_discrete(name = "")

g <- g + theme_bw()

print(g)

Rplot.png

...ほらね？

2018/07/31: SASのコード、Rによるシミュレーションをつけ加えました。

雑記：データ解析 - 覚え書き：層別抽出標本から母分散を推定する方法(シミュレーションつき)

　変数$X, Y$の共分散は、ご存じのように「ある人のXから平均を引き、Yから平均を引き、このふたつを掛けた値の平均」、つまり
　$cov(X, Y) = (1/N) \sum_i^N (x_i - \bar{x})(y_i - \bar{y})$
である。これは「ある人のXとYを掛けて平均し、Xの平均とYの平均の積を引いた値」すなわち
　$cov(X, Y) = (1/N) \sum_i^N x_i y_i - \bar{x} \bar{y}$
とも書き換えられますわね。さすがにここまでは学生時代に習った気がする。

　さて、この中身をさらに$N$倍しますやんか？
　$cov(X, Y) = \ (1/N^2) \left( N\sum_i^N (x_i y_i) - \sum_i^N x_i \sum_i^N y_i \right)$
　大かっこの中身に注目。
　第1項の$N\sum_i^N (x_i y_i)$とはなにか。たとえば$N=3$ならば、これは
　$3 (x_1 y_1 + x_2 y_2 + x_3 y_3)$
　$= (x_1 y_1 + x_2 y_2 + x_3 y_3) + (x_1 y_1 + x_2 y_2) + (x_1 y_1 + x_3 y_3) + (x_2 y_2 + x_3 x_3)$
　と書き直せる。つまり、まずすべての$x_i y_i$を並べ、次に$i$と$j (\geq i)$について$(x_i y_i + x_j y_j)$を並べる形に書き直せる。なぜこんなことをしているのか？ 我慢して先に進みましょう。
　第2項の$\sum_i^N x_i \sum_i^N y_i$とはなにか。$N=3$ならば
　$(x_1 + x_2 + x_3)(y_1 + y_2 + y_3)$
　$= (x_1 y_1 + x_2 y_2 + x_3 y_3) + (x_1 y_2 + x_2 y_1) + (x_1 y_3 + x_3 y_1) + (x_2 y_3 + x_3 y_2)$
と書き直せる。つまり、まずすべての$x_i y_i$を並べ、次に$i$と$j (\geq i)$について$(x_i y_j + x_j y_i)$を並べる形に書き直せる。
第1項から第2項を引くと何が起きるか。最初の$(x_1 y_1 + x_2 y_2 + x_3 y_3)$は消える。そこから先は
　$(x_1 y_1 + x_2 y_2) - (x_1 y_2 + x_2 y_1) $
　$+ (x_1 y_1 + x_3 y_3) - (x_1 y_3 + x_3 y_1) $
　$+ (x_2 y_2 + x_3 y_3) - (x_2 y_3 + x_3 y_2) $
おおお、なんということでしょう。上の3行のいずれも、$(x_i -x_j)(y_i - y_j)$ではありませんか。

　というわけで、
　$cov(X, Y) = \ (1/N^2) \sum_{i=1}^N \sum_{j=i+1}^N (x_i - x_j)(y_i - y_j)$
つまり、共分散とは「異なる2人を連れてきて、$X$の差と$Y$の差の積を求め、これを全ペアを通じて合計し、人数の二乗で割ったもの」でもあるのだ。

　...こういう話を前にどこかで読んだことがあったんだけど、フーン面白いね、と聞き流していた。このたび仕事の都合で調べものをしていて、最初から分散を(偏差じゃなくて)ペアの差で定義している文献があって、困ってしまった次第である。深夜から早朝に掛けての数時間を費やした検索と苦悩の末、なんとか理解が追い付いたので、自分のためにメモしておく。
　参考文献は
Zhang, Wu, Cheng (2012) Some New Deformation Formulas about Variance and Covariance. Proc. 4th Int. Conf. Modelling, Identification and Control, 1042-1047
なのだが、これはたまたまみつけただけで(Wikipediaに載っていた...)、おそらくどこかの統計学の教科書に書いてあるような話なのだろう。

　なにしろきちんとした教育を受けていないもので、これがどのくらいのレベルの話なのか、よくわからない。実は、理系の学生さんならみんな知ってる話だったりしてね！ はっはっは！ そういうの困っちゃうよね！

雑記：データ解析 - 覚え書き：差の集計としての共分散

2018年7月26日 (木)

Bethel, J. (1989) Sample allocation in multivariate surveys. Survey Methodology, 15(1), 47-57.
　仕事の都合で読んだ。題名の通り、標本抽出設計における最適割当法(層とかクラスタとかに割り当てる標本サイズを、単に母集団サイズに比例させるんじゃなくて、コストまで考慮してもっとゴリゴリ考える奴) についての論文。
　著者はWestatの人。掲載誌はカナダ統計局の機関誌だと思う。

　いわく。
　多目的的な調査における標本の最適割当問題について最初に論じたのはNeyman(1934)であった。以来、この問題へのアプローチは次の2つに大別される。

　本論文では線形不等性制約のもとでの最適割り当てを閉形式で与える。本研究の利点は...[略]

　層別無作為抽出について考える。層の数を$I$, 変数の数を$J$とする。層$i$における$j$番目の変数の分散を$S^2_{ij}$, 層の標本サイズを$n_i$, 母集団に占める層の割合を$W_i$とする[原文では$W^2_i$となっているがミスプリであろう]。有限母集団修正は無視できるものとする。
　いま、次の制約が課せられているとする。任意の正の定数$v_j$について、
　$Var(\bar{y}_j) \approx \sum_i W^2_i S^2_{ij} / n_i \leq v^2_j$
以下では
　$a_{ij} = W^2_i S^2_{ij} / v^2_j$
と定義し[原文では$W$は小文字だが直した]、これを「標準化精度単位」と呼ぶ。$a_{ij} \geq 0$である。$\mathbf{a}_j = (a_{1j}, \ldots, a_{Ij})^T$とする。

　コスト関数を定義しよう。$x_i = 1/n_i$($n_i$が0なら無限大)として
　$g(\mathbf{x}) = \sum_i c_i / x_i, \ \ c_i > 0$
とする[要するに票単価を$c_i$としますってことね]。固定コストをいれてもいいけど以下の話には影響しない。

　この最適割当問題は以下のように定式化できる。
　Minimize $g(\mathbf{x})$
　subject to
　　$\mathbf{a}_j^T \mathbf{x} \leq 1, \ \ j=1,\ldots, J$
　　$\mathbf{x} > 0$

　さて、単一変数の最適割当についてはすでに良く知られている。$J=1$のときの上の問題の解$\mathbf{x}^*$は, すべての$i$について$a_{i1} > 0$のときにのみ有限となり
　$x^*_i = \sqrt{c_i} / \left( \sqrt{a_{1i}} \sum_k \sqrt{c_k a_{k1}} \right)$
である。
　これを$J > 1$へと拡張すると... [省略するけど、拡張できるんだそうです]

　$v_i$をちょっぴり動かしたらコストがどう変わるか...[これをシャドー・プライスと呼ぶ由。へー。内容のメモは、まあいいや、省略]
　最適化プログラミングにおける注意点 ... [パス]
　考察...[パス]

　。。。というわけで、こりゃあ私の能力を超える内容だ、と早々に見切ってしまったのだが、最適割当という問題に対する土地勘を養いたかっただけなので、この論文はこれでよし、ってことにしましょー。

論文：データ解析(2018-) - 読了: Bethal (1989) 目的変数が複数ある調査の標本抽出設計における最適割当法

2018年7月23日 (月)

堤盛人・瀬谷創 (2012) 応用空間統計学の二つの潮流：空間統計学と空間計量経済学. 統計数理, 60(1), 3-25.
　これもしばらく前にめくったやつ。瀬谷・堤「空間統計学」の基になっているような感じの内容であった。

論文：データ解析(2018-) - 読了：堤・瀬谷(2012) 空間統計学と空間計量経済学

久保川達也 (2006) 線形混合モデルと小地域の推定. 応用統計学, 35(3), 139-161.
　小地域推定についての解説論文。Rao & Molina本を読む前に目を通した気がするんだけど、記録がないので、整理の都合上読み直した。
　いくつかメモ：

論文：データ解析(2018-) - 読了：久保川(2006) 線形混合モデルで小地域推定

2018年7月20日 (金)

Chandra, H., Kumar, S., Aditya, K. (2016) Small area estimation of proportions with different levels of auziliary data. Biometrical Journal, 60(2), 395-415.
　二値データの小地域推定について、推定方法をシミュレーションで比較した実験。仕事の都合で、まさにこういうのを探していたんです。著者らはインド・ニューデリーの人。ありがとう、インドの先生。
　ちょっと細かめにメモを取った。

1. イントロダクション
　二値データの小地域推定、つまり小地域における割合の推定においては、ロジット・リンクの一般化線形混合モデル(GLMM)が用いられることが多い。ユニットレベル共変量がある場合、小地域における割合の推定には経験的プラグイン予測量(EPP)が使われることが多い。実はMSEを最小化する推定量は他にあるのだが(経験的最良予測量, EBP)、閉形式でなく数値近似が必要なのであまり使われていない。
　一般に小地域モデルは地域レベルとユニットレベルに大別される。地域レベルではFay-HerriotモデルによるEBLUP推定量が知られている。地域レベルモデルもユニットレベルモデルも線形混合モデルの特殊ケースである。
　二値の場合、地域レベルでもユニットレベルでも、結局はロジット・リンクのGLMMが使われているわけだが、ユニットレベルモデルのEPPと地域レベルモデルのEPPは異なる。最近では地域レベルポアソン混合モデルのEBPというのも開発されている。
　二値データの場合、どういう共変量があったらどういう推定量を使うべきか。本論文では、ロジット・リンクのGLMM(すなわちロジスティック正規混合モデル)のもとでのいろんな推定量について述べる。

2. 小地域推定
　母集団$U$(サイズ$N$)が、小地域$U_1, \ldots, U_D$(サイズ$N_1, \ldots, N_D$)に重なりなく完全に分割されているとする。母集団から標本$s$(サイズ$n$)を取ってきた。小地域別にみると$s_1, \ldots, s_D$(サイズ$s_1, \ldots, s_D$)である。抽出されなかった残りの部分を$r_1, \ldots, r_D$とする。
　小地域$i$のユニット$j$の関心ある変数の値を$y_{ij}$とする。本論文ではこれを二値とする。
　いま推測したいのは$P_i = (1/N_i) \sum_{j \in U_i} y_{ij}$である($U_i$は$s_i$と$r_i$からなるという点に注意)。

　デザインベース直接推定量(DIR)は
　$\hat{P}^{DIR}_i = \sum_{j \in s_i} w_{ij} y_{ij}$
と書ける。ここで$w_{ij}$は調査ウェイトで、$\sum_{j \in s_i} w_{ij} = 1$と基準化されている。
　$\hat{P}^{DIR}$のデザインベース分散は
　$var(\hat{P}^{DIR}_i) \approx \sum_{j \in s_j} w_{ij}(w_{ij}-1)(y_{ij} - \hat{P}^{DIR}_i)^2$
と近似できる。
　SRSならば、
　$\hat{P}^{DIR}_i = (1/n_i) \sum_{j \in s_i} y_{ij}$
　$var(\hat{P}^{DIR}_i) \approx (1/n_i) \hat{P}^{DIR}_i (1-\hat{P}^{DIR}_i)$
である。
　
　では小地域モデルについて。
　ユニットレベル共変量を$\mathbf{x}_{ij}$(長さ$p$)とする[書いてないけどどうやら切片項もコミである]。$\pi_{ij} = Prob(y_{ij} = 1)$として、ロジットリンクGLMM
　$logit(\pi_{ij}) = \mathbf{x}^T_{ij} \mathbf{\beta} + u_i, \ \ u_i \sim N(0, \sigma^2)$
を考える。$u_i$は互いに独立。[←ここで$j$が$N_i$まで動く点に注意。つまりこれは母集団モデルである]
　
　このモデルによる経験的プラグイン予測量(EPP)は
　$\hat{P}^{EPP}_i = (1/N_i) (\sum_{j \in s_i} y_{ij} + \sum_{j \in r_i} \hat{\mu}_{ij})$
ただし$\hat{\mu}_{ij} = logit^{-1} (\mathbf{x}^T_{ij} \hat{\beta} + \hat{u}_i)$である。
　[原文では、$\hat{\mu}_{ij} = \exp(\mathbf{x}^T_{ij} \hat{\beta} + \hat{u}_i) / (1+\exp(\mathbf{x}^T_{ij} \hat{\beta} + \hat{u}_i))$とあるけれど、書くのが面倒なので$logit^{-1}(\cdot)$と略記する。以下同様]
　ここで$\hat{\beta}$は固定効果パラメータの推定値、$\hat{u}_i$はランダム効果パラメータの予測値である。
　GLMMの推定手続きとしてもっともよく使われているのはPQLである。この方法では、反応変数の非正規な分布を線形近似し、線形化された従属変数が近似的に正規分布に従うと仮定する。場合によっては一致性・不偏性が失われるものの、経験的には上手くいく。

　ここからは、共変量の入手可能性に応じた、３つのケースについて考える。

　ケース1、標本ユニットでのみ共変量が入手可能であるケース。
　この場合、モデルのあてはめは可能だが、EPPは手に入らない。そこで次の推定量(EPP1)を提案する。
　$\hat{P}^{EPP1}_i = \sum_{j \in s_i} w_{ij} \hat{\mu}_{ij}$
EPP1はDIRより効率的だが、モデルの誤指定によるバイアスはDIRより大きい。EPP1は、標本抽出ウェイトに対応する回数だけ共変量の値を反復し、共変量のセンサスを再作成し、このセンサスを使って、ロジット混合モデルで確率を予測していることになる[←ややこしい...]
　EPP1の欠点は、標本ユニットのアウトカムを使っていない点である。
　[↑そりゃそうだよなあ、これは変だ。もっと良い推定量があるんじゃなかろうか...]

　ケース2, 標本ユニットで共変量が入手可能で、かつそれらの共変量の母集団での集計値が入手可能であるケース。
　$\bar{\mathbf{X}}_i = (1/N_i) \sum_{j \in U_i} \mathbf{x}_{ij}$, $\bar{\mathbf{x}}_i = (1/N_i) \sum_{j \in s_i} \mathbf{x}_{ij}$とすると、ここから非標本ユニットにおける平均$\bar{\mathbf{X}}_{r_i}$がわかる[面倒なので式は省略するが、そりゃわかるよな]。
　まずモデルをあてはめて$\hat{\beta}$, $\hat{u}_i$を得る。で、$\hat{\mu}^{EPP2}_{ij} = logit^{-1} (\bar{\mathbf{X}}^T_{r_i} \hat{\beta}+ \hat{u}_i)$を求める。推定量は
　$\hat{P}^{EPP2}_i = (1/N_i) (\sum_{j \in s_i} y_{ij} + \sum_{j \in r_i} \hat{\mu}^{EPP2}_{ij} )$
　標本平均$p_i = (1/n_i) \sum_{j \in s_i} y_{ij}$, 標本抽出割合$f_i = n_i / N_i$を使って書き直すと
　$\hat{P}^{EPP2}_i = f_i p_i + (1-f_i) \hat{\mu}^{EPP2}_{ij}$
$f_i$が小さく、かつ$\bar{\mathbf{X}}_i \approx \bar{\mathbf{X}}_{r_i}$なら、$\bar{\mathbf{X}}_{r_i}$の代わりに$\bar{\mathbf{X}}_i$を使って
　$\hat{P}^{EPP2.1} = f_i p_i + logit^{-1} (\bar{\mathbf{X}}^T_i \hat{\beta} + \hat{\mathbf{u}}_i)$
でもよい。$f_i$が無視できる大きさなら、
　$\hat{P}^{EPP2.2} = logit^{-1} (\bar{\mathbf{X}}^T_i \hat{\beta} + \hat{\mathbf{u}}_i)$
でもよい。

　ケース3, 共変量の母集団集計値だけが入手可能であるケース。
　この場合はさきほどのモデルのあてはめ自体が無理で、
　$logit(\pi_{ij}) = \bar{\mathbf{X}}^T_i \mathbf{\alpha} + v_i, \ \ v_i \sim N(0, \sigma_v^2)$
をあてはめるしかない。で、$\hat{\mu}^{EPP3}_{ij} = logit^{-1} (\bar{\mathbf{X}}^T_i \hat{\alpha}+ \hat{u}_i) $ を求める。推定量は
　$\hat{P}^{EPP3}_i = (1/N_i) (\sum_{j \in s_i} y_{ij} + \sum_{j \in r_i} \hat{\mu}^{EPP3}_{ij} ) = f_i p_i + (1-f_i) \hat{\mu}^{EPP3}_{ij}$
となる。標本抽出割合が無視できる大きさなら、
　$\hat{P}^{EPP3.1}_i = \hat{\mu}^{EPP3}_{ij}$
でもよい。これはEPP2.2と同じになるけど、元のモデルは異なる。[ああそうか。どちらも横着して非標本ユニットだけに注目している点では同じだが、EPP2.2は非標本ユニットにおける共変量の母平均を考えるのが面倒だから全体の母平均を使っているのに対して、EPP3.1は最初から全体の母平均しかわかんないわけだ]

　...という路線のほかに、ふたつ代替路線がある。両方とも、ケース2と3で使える。
　代替路線その１，地域レベルでモデルを組む。
　$logit(\pi_i) = \bar{\mathbf{X}}^T_i \lambda + a_i, \ \ a_i \sim N(0, \sigma_a^2)$
とする。推定量は
　$\hat{P}^{EPP.A}_i = logit^{-1} (\bar{\mathbf{X}}^T_i \hat{\lambda}+ \hat{a}_i)$
となる。まず$\sigma_a^2$をREML推定し、次に$\lambda$と$a_1, \ldots, a_D$を
PQL推定する。詳細はChandra et al. (2011 J.App.Stat.), Johnson et al. (2010 J.Official Stat.)をみよ。
　代替路線その２，Fay-Herriotモデルを組んじゃってEBLUP推定量を使う(EBLUP.FH)。これは推定値が$[0,1]$の外側に出ちゃうかもしれない。[Fay-Herriotモデルの場合、小地域ごとの標本抽出誤差の分散が既知でないといけないと思うんだけど、そこはどうやったんだろう？ $n_i p_i (1-p_1)$としたのかな？]

　[話が長くなってしまったので、EBLUP.FHを除くすべての推定量を同一の記法で書き直しておく。なお、
　$logit(\pi_{ij}) = \mathbf{x}^T_{ij} \mathbf{\beta} + u_i, \ \ u_i \sim N(0, \sigma^2)$
　$logit(\pi_{ij}) = \bar{\mathbf{X}}^T_i \mathbf{\alpha} + v_i, \ \ v_i \sim N(0, \sigma_v^2)$
である。うーん、こうしてみると、標本ウェイトがEPP1でしか使われていないという点も不思議だなあ...]

3. MSE推定[略]

4. シミュレーション
　というわけでシミュレーションをふたつやります。(1)モデル・ベース・シミュレーション。データ生成モデルをつくって母集団を都度生成する。(2)デザイン・ベース・シミュレーション。実データを母集団にみたてて標本抽出する。
　まず評価基準を定義しておく。
　$k$回目の反復における小地域$i$の割合を$p_{ik}$とする[直接推定量ではなくて母平均のことらしい。よってデザインベースの場合は$k$を通じて同一]。その推定値を$\hat{p}_{ik}$, MSE推定値を$mse_{ik}$とする。$p_{ik}$の全$K$回を通じた平均を$P_i$とする[デザインベースの場合は$p_i$と等しいってことでしょうね]。
　推定量のMSEの推定値を$mse_{ik}$, 真値を$MSE_i = mean_k ( (\hat{p}_{ik} - p_{ik})^2 )$とする。
　[以下、簡略のため $(1/K)\sum_k^K(\cdot)$を$mean_k (\cdot)$と略記する]

　シミュレーション１，モデルベース・シミュレーション。
　$D=30, N_i=500$とする。母集団生成モデル(後述)に従って母集団を生成し、地域を層にした層別無作為抽出で標本を抽出し、いろんな推定量で推定する。以上を$K=1000$回繰り返す。
　分析モデルは：
　$y_{ij} \sim Binomial(1, \mu_{ij})$
　$\mu_{ij} = logit^{-1} (1+x_{ij} + u_i)$
　$u_i \sim N(0, \sigma^2)$ (iid)
　$x_{ij} \sim \chi^2(1)$ (iid)

　要因は：

[他にMSE評価のために別のシミュレーションをやっているけど、省略]

　結果。
　[ここでは考察はなく、表のみ示されている。表を眺めていて結構びっくりしたので、メモしておく。
　推定量のパフォーマンス(Table 1), $n_i=5, \sigma^2=0.25$をみると、まずEBLUP.FHはバイアスRB(P)が法外に大きいので除外してよい。他の推定量について分散RRMSE(P)を比べると、DIRが20.3, EPPが9.2。肝心の提案推定量は、EPP1, EPP2系, EPP3系がいずれも10から12なのに対して、なんとEPP.Aの成績が良い(9.56)。かつ、EPP2系はなぜかバイアスRB(P)が大きくなるのに対して、EPP.AはバイアスにおいてもDIRと遜色ない小ささを誇る。つまり、EPP.A (地域レベルGLMM)の成績は、EPP(ユニットレベルGLMM)に匹敵するのである。
　まじか。それって、仮に共変量の母平均$\bar{\mathbf{X}}_i$が手に入っている場合(たとえば小地域が国勢調査小地域、共変量が性年代だというような場合)、非標本の共変量がわからないならば、たとえ標本の共変量をユニットレベルで測っていたとしても(ケース2)、それを捨てて地域レベルGLMMを組んだほうがよい、ということだ。言い換えると、$y_{ij}$と$x_{ij}$の地域内での共分散は捨てて良いということだ。不思議だ...
　このメモは論文を一通り読み終えてから書き直しているので、ここで感想をメモしておくと、上記の知見がどこまで一般化可能なのかという点について非常にもやもやした気持ちが残る。頭が整理できていないんだけど、生成モデルにおいて共変量が地域と直交しているという点がどうもひっかかる。このとき、$y_{ij}$と$x_{ij}$の地域内での共分散は存在するいっぽう、($N_i$が十分に大きければ)小地域特性の予測に共変量は効かないわけだ。だからどうだと論理的に説明できないんだけど、これってすごく特殊な状況なのではないかと...]

　シミュレーション２，デザインベース・シミュレーション。
　インドのNational Sample Survey Office (NSSO)による、ビハール州のdebt investment についての標本調査データを使う。38地域, 母集団サイズは52～140。ここから20件づつ層別無作為抽出して分析する。
　目的変数は「世帯が貸付残高を持っているか」。共変量は所有している土地の広さ。
　[面倒になってきたのでここからのメモは省略するが、動かすのは標本サイズだけである]

　結果の考察。
　推定量についてみると、

　MSEについてみると、

5. 実データへの適用[略]

6. 結論
　提案手法はEPPのかわりとして使えることがわかった。EPP1のMSEも使えることがわかった。
　今後の課題: 空間モデルへの拡張、よりよいMSE推定の開発。

　... やれやれ、疲れた。
　
　論文の内容に対する疑問をメモしておくと：(1)ベイジアンならどうなるのか。これは自分で試せって話でしょうね。(2)上にメモしたように、なぜEPP.Aの成績がよいのかという点に興味を惹かれる。

　実のところ、この論文を読んだ最大の理由は、すべてのシミュレーションのRコードが公開されているという点にある。そういうの、ほんとに助かります。まだちゃんとみてないけど、lme4パッケージを使っているようだ。

論文：データ解析(2018-) - 読了：Chandra, Kumar, Aditya (2018) 二値データの小地域推定

2018年7月13日 (金)

Wall, M.M. (2004) A close look at the spatial structure implied by the CAR and SAR models. Journal of Statistical Plannning and Inference, 121, 311-324.
　仕事の合間に読んだ奴。空間計量経済学でいうところのSARモデル(同時自己回帰モデル)とCARモデル(条件つき自己回帰モデル)は、特に不規則格子に適用したとき、意外な相関構造をもたらすよ、という論文。
　なんの気なしに読み始めたら、これがほんとに面白くって... 最後まで一気読みしてしまった。

　説明の都合上、まずはモデルの定式化から。
　$\{A_1, \ldots, A_n\}$が$D$の格子になっているとする(つまり、$D$を重なりなく完全に分割しているとする)。$\{Z(A_i): A_i \in (A_1, \ldots, A_n)\}$をガウス過程とする。
　[以下、本文ではいちいち$Z(A_i)$と書いているけど、うざいので$Y_i$と略記する]

　SARモデルとは、
　$Y_i = \mu_i + \sum_j^n b_{ij} (Y_j - \mu_j) + \epsilon_i$
　$\mathbf{\epsilon} = (\epsilon_1, \ldots, \epsilon_n)' \sim N(\mathbf{0}, \mathbf{\Lambda})$
ただし$\mathbf{\Lambda}$は対角行列。$\mu_i = E[Y_i]$。$b_{ij}$は定数で($b_{ii}=0$)、既知でも未知でもよい。[この定式化だと、空間自己回帰パラメータは$b_{ij}$のなかに入ってるわけね]
　$n$が有限なら、$\mathbf{Y} = (Y_1, \ldots, Y_n)'$, $\mathbf{\mu} = (\mu_1, \ldots, \mu_n)'$, $\mathbf{B} = (b_{ij})$として
　$\mathbf{Y} \sim N(\mathbf{\mu}, (\mathbf{I} - \mathbf{B})^{-1} \mathbf{\Lambda} (\mathbf{I} - \mathbf{B})^{-1'})$
である。$\mathbf{B}$は、隣接行列を$\mathbf{W}$として$\mathbf{B} = \rho_s \mathbf{W}$とすることが多い。この場合
　$\mathbf{Y} \sim N(\mathbf{\mu}, (\mathbf{I} - \rho_s \mathbf{W})^{-1} \mathbf{\Lambda} (\mathbf{I} - \rho_s \mathbf{W})^{-1'})$
である。

　CARモデルでは、$Y_{-i} = \{Y_j: j \neq i\}$と書くとして
　$Y_i | Y_{-i} \sim N \left( \mu_i + \sum_j^n c_{ij} (Y_j - \mu_j), \tau^2_i \right)$
ただし、$\mu_i = E[Y_i]$。$c_{ij}$は定数で($c_{ii}=0$)、既知でも未知でもよい。
　$n$が有限なら、$\mathbf{C} = (c_{ij})$とし、対角に$\tau_i^2$を持つ対角行列を$\mathbf{T}$として
　$\mathbf{Y} \sim N(\mathbf{\mu}, (\mathbf{I} - \mathbf{C})^{-1} \mathbf{T})$
である。$\mathbf{C}$は、隣接行列を$\mathbf{W}$として$\mathbf{C} = \rho_c \mathbf{W}$とすることが多い。この場合
　$\mathbf{Y} \sim N(\mathbf{\mu}, (\mathbf{I} - \rho_c \mathbf{W})^{-1} \mathbf{T})$
である。

　隣接行列$\mathbf{W}$の要素$w_{ij}$は、隣だったら1, そうでなかったら0とすることが多いが、行の和を1にしたり、もっといろいろ工夫することもある。行で基準化する理由は、近接地域の数が変動するときに内的整合性が失われるからである。
　なお、CARモデルでは$\mathbf{W}$と$\mathbf{T}$が$w_{ij} \tau_j^2 = w_{ji} \tau_i^2$を満たさなければならない。
　
　なお、CARをもっと限定したICAR(intrinsic CAR)モデルもあるが、ここでは扱わない。

　準備はできた。ここからが本題。

　米48州のSAT言語得点平均をモデル化してみる。共変量は受験率とし(中部の州は受験率が低く得点平均が高い)、二次の項もいれる。
　誤差項について次の4つのモデルを比較する。

　誤差項の予測値を比較すると、SARとCARはだいたい同じで(CARのほうが分散が大きい)、バリオグラムモデルとはずいぶんちがう。よくみると、SARとCARでは隣接している2州のあいだでも相関がちがっている[ああそうか、州の形が不規則だからね]。バリオグラムモデルの場合は経験バリオグラムをみれば残差の空間構造が適切かどうかチェックできるが、SARとCARでは共分散に体系的な構造がなく、それが空間構造の記述として適切かどうかを調べる方法がないのである。[←なるほどー]

　こんどは、同じ米48州の隣接行列$\mathbf{W}$を使って、SARとCARの共分散行列が$\rho_s, \rho_c$とともにどう変わるかを調べてみよう。つまりこれはデータと関係ない話である。
　$\rho_s$と$\rho_c$がとりうる範囲は、$\mathbf{W}$の固有値を$\omega_i$として、$i=1, \ldots, n$について$\rho_s \omega_i < 1$, $\rho_c \omega_i < 1$である、と通常考えられている。厳密にいうと、SARモデルの場合には$\rho_s \neq 1/\omega_i$が満たされていればよいのだが、$\rho_s$の解釈が難しくなる。[...このくだり、理解が追いつかない。あとで勉強しておこう。Haining(1990)という教科書がreferされている]
　まあとにかく、この米48州の隣接行列でいえば、$\rho_s, \rho_c$は(-1.392, 1)の範囲を動ける。
　$\rho_s, \rho_c$を動かしながら、隣接州(107ペア)の相関がどうなるかをチャートにしてみると、面白いことがわかる。
　$\rho_s, \rho_c$が0のとき、隣接州の相関は0になる。増やしていくと相関も単調に上がっていき、1まで増やせばみんな相関1になる。なお、CARモデルで$\rho_c$を増やした時よりも、SARモデルで$\rho_s$を増やしたときのほうが、隣接州の相関は速く上がる。ここまでは、まあ、いいですよね。
　問題はここからだ。隣接州107ペアの相関の高さの順序は一定でない。$\rho_s$なり$\rho_c$なりを増やしていくと、順序がどんどん入れ替わっていくのだ。
　さらに。$\rho_s, \rho_c$を負の方向に動かした時は奇妙なことが起こる。最初はどのペアの相関も負になっていくが、途中から突然正の相関を持つペアが生じるのである。結局、107ペアのうち37ペアは正になる。どういうペアが正になるかを簡単に説明する方法はない。
　
　このように、SARモデル・CARモデルによる空間相関は直観に反する。なお、これは$\mathbf{W}$の行規準化をやめても変わらない。

　かつてCressie(1993)は、$\mathbf{B}, \mathbf{C}$を「空間従属行列」と呼んだ。この行列の要素$(i,j)$は、地点$i, j$の相互作用の程度を表現していると考えられてきた。そういう言い方は実はミスリーディングである。空間構造を本当に説明しているのは$(\mathbf{I} - \mathbf{B})^{-1}$, $(\mathbf{I} - \mathbf{C})^{-1}$である。$\mathbf{B}, \mathbf{C}$と空間相関のあいだに直観的な関係はない。空間構造に関心があるなら、地球統計学のモデルのように、共分散構造を直接モデル化する手を考えたほうが良い。

　SARモデル・CARモデルは広く使われているが、その意味についてきちんと考えている人は少ない。これはおそらく、分析者の関心が空間構造そのものというより回帰の予測子に向けられているからだろう。しかし！もしあなたが、モデルがデータに合致しているかどうかを決めようという立場なら、まずはモデルの意味を知ろうとしたほうがいいんじゃないですか？
　云々。

　。。。いやー、これは面白かった。
　このたび小地域推定の関連で勉強していて、SARモデルやCARモデルって直観的にはどういうことなのだろうかと不思議に思っていたのである。だって、どちらもローカルな空間的従属性についてモデル化しているのに、結局は大域的な相関構造が生まれるじゃないですか。隣接行列をいくら思い返しても、相関行列が想像できない。そうか、あれは直観的にわかる話ではないのね。謎が氷解したという感じだ。
　空間自己相関パラメータが負になった時にとんでもないことが起きるというのも面白かった。たしかにね、地域の形が不規則だったら、なにが起きても不思議でない。
　というわけで、きちんと積み上げて勉強している人にとっては当たり前の話をしているのかもしれないけど、私のように付け焼刃だけで凌いでいる者にとっては、とても啓蒙的な論文であった。思わずwebで写真を探してしまった(町内会の会合にクッキー持ってきそうな、気の良さそうな女性であった)。メラニー先生、どうもありがとー。

論文：データ解析(2018-) - 読了: Wall (2004) SARモデル・CARモデルは実は君が思っているような空間モデルではないかもしれないよ？

2018年7月10日 (火)

　これは徹頭徹尾自分向けのメモでございます。
　仕事の都合で空間計量経済学の資料をあたっていると、XXXモデルという英字三文字の略語が乱舞し、しかもその意味が人によってかなりちがっていたりする。
　許すまじ学者ども、とっつかまえて海の藻屑にしてやろうか、と腹を立てていたのだが、怒っていてもらちがあかないので、メモをとってみた。とりあえず、いま手元にある3冊のデータ解析者向け解説書の記述を比較しておく。

瀬谷・堤(2014)「空間統計学」
　6.1, 6.2.1, 6.2.2よりメモ。

　いわく。格子データのモデリングは大きく次の２つに分類できる。

　というわけで、以下では後者について解説する。

　空間計量経済学においては、空間自己相関をモデル化する際、次の2つのモデルがよく用いられる。

1. 空間ラグモデル(spatial lag model, SLM)。mixed regressive spatial autoregressive model, spatial autoregressive model(SAR)と呼ばれることもある。

　SLMでは従属変数間に自己相関を導入する。空間的・社会的な相互作用の結果として生じた「均衡」のモデル化だといえる。一般的な形式としては
　$y_i = g(y_{j \in S_i}) + \beta_0 + \sum_h x_{hi} \beta_h + e_i$
ふつうは空間重み行列を使って単純化する。
　$y_i = \rho \sum_j^n w_{ij} y_j + \beta_0 + \sum x_{hi} \beta_h+ e_i$
右辺に$y$の空間ラグがあるという意味では時系列でいう自己回帰と似ている。
　行列で書くと
　$\mathbf{y} = \rho \mathbf{W} \mathbf{y} + \mathbf{X} \mathbf{\beta} + \mathbf{e}$

2. 空間誤差モデル(spatial error model, SEM)。これがsimultaneous autoregressive model(SAR)と呼ばれていることもある。

　SEMでは誤差項間に自己相関を導入する。経済理論的な理由というより、空間的に系統性のある観測誤差といったデータの問題を処理するために用いられることが多い。
　誤差項のモデル化の方法にはたくさんある。4つ紹介するが、いちばん良く用いられているのは2-1.SAR誤差である。

2-1. SAR誤差(spatial autoregressive)。これを狭義のSEMと呼ぶこともある。
　$\mathbf{y} = \mathbf{X} \mathbf{\beta} + \mathbf{u}, \ \ \mathbf{u} = \lambda \mathbf{W} \mathbf{u} + \mathbf{e}$
$\mathbf{u}$の共分散行列は
　$E[\mathbf{uu}'] = \sigma_e^2(\mathbf{I}-\lambda \mathbf{W})^{-1} (\mathbf{I}-\lambda \mathbf{W'})^{-1}$
となる。ここで$(\mathbf{I}-\lambda \mathbf{W})^{-1}$を空間乗数という。$\mathbf{I}-\lambda \mathbf{W}$が正則であることが求められる。
　SAR誤差モデルの場合、ある地点のショックが他のすべての地点に波及する。また、地点の近傍集合の個数が地点によって違うとき、たとえ$e$がiidであっても$\mathbf{u}$の分散は不均一になる。

2-2. SMA誤差(spatial moving average)。
　$\mathbf{u} = \gamma \mathbf{W} \mathbf{e} + \mathbf{e}$
$\mathbf{u}$の共分散行列は
　$E[\mathbf{uu}'] = \sigma_e^2(\mathbf{I}+\gamma \mathbf{W})(\mathbf{I}+\gamma \mathbf{W})'$
　ある地点におけるショックは、$\mathbf{W}$を通した1次の影響と, $\mathbf{WW}'$を通した2次の影響しかもたない。なお、SAR誤差と同じく、地点の近傍集合の個数が地点によってちがうと共分散は定常でなくなる。

2-3. SEC誤差(spatial error component)。
　$\mathbf{u} = \mathbf{W} \mathbf{\phi} + \mathbf{e}$
誤差をスピルオーバーする部分$\mathbf{\phi}$としない部分$\mathbf{e}$に分けている。$\mathbf{\phi}$と$\mathbf{e}$の各要素はiidで、2本のベクトル間に相関はないと考える。
$\mathbf{u}$の共分散行列は
　$E[\mathbf{uu}'] = \sigma_\phi^2 \mathbf{WW}' + \sigma_e^2 \mathbf{I}$
　SEC誤差はもともとSAR誤差の代替案として提案されたものであった。$(\mathbf{I}-\lambda \mathbf{W})$は正則でなくてもよい。しかし共分散行列をみると、局所的相関しか考慮していないわけで、むしろSMA誤差に近い。

2-4. CAR誤差(conditonal autoregressive)。
　これはSAR誤差との対比で紹介されることが多い。SAR誤差では$\mathbf{u}$の同時分布をモデル化したが、ここでは近隣集合の下での条件付き分布をモデル化する。
　$E(u_i | u_j, j \neq i) = \eta \sum_j w_{ij} u_j$
$\mathbf{W}$にいくつか制約をつけると、
　$E[\mathbf{uu}'] = \sigma^2 (\mathbf{I} - \eta \mathbf{W})^{-1}$
となる。
　[話がすごくややこしいが、2.の空間誤差モデルの一部ではあるものの、2-1,2-2,2-3のような同時自己回帰モデルではないわけだ]

3. SLM(空間ラグモデル)とSEM(空間誤差モデル)の複合型もある。

3-1. 一般化空間モデル(SACモデル)。
　[別の資料によれば、SACとはgeneral spatial autoregressive model with a correlated error termの略である由。] SARARモデルともいう(spatial autoregressive model with spatial autoregressive disturbances)。
　$\mathbf{y} = \rho \mathbf{W} \mathbf{y} + \mathbf{X} \mathbf{\beta} + \mathbf{u}, \ \ \mathbf{u} = \lambda \mathbf{W} \mathbf{u} + \mathbf{e}$
　空間ラグモデルと空間誤差モデル(SAR誤差)をあわせたものになっている。

3-2. 空間ダービンモデル(spatial Durbin model, SDM)。
　$x$は定数項抜きとして、
　$\mathbf{y} = \rho \mathbf{W} \mathbf{y} + \mathbf{X} \mathbf{\beta} + \mathbf{W x \delta} + \mathbf{e}$
　SACモデルから$\mathbf{W u}$を落として、かわりに従属変数と説明変数の空間ラグをいれているわけだ。実はこのモデル、SAR誤差モデルから導くことができる。

古谷(2011)「Rによる空間データの統計分析」

上記のメモとの対応は以下の通り。

谷村(2010)「地理空間データ分析」

上記のメモとの対応は以下の通り。

雑記：データ解析 - 覚え書き: 空間計量経済学における忌まわしき英字三文字略語たち

2018年7月 3日 (火)

Bookcover Small Area Estimation (Wiley Series in Survey Methodology) [a]
Rao, J. N. K.,Molina, Isabel / Wiley / 2015-08-24
ここ２週間ほど、常にこの本を携帯し、少しの時間でもあれば頁を開き、寝ても覚めても小地域推定のことばかり考えていた。仕事の都合での勉強ではあったのだが、いいかげん他の仕事も詰まってきたし、考えれば考えるほど難しくて吐きそうになり、いまや日常生活にも支障が生じ始めた。いったんここでやめて、少し頭を冷やすことにする。
　読書ノートはこちら。読み返すと、学力不足で理解に達していない箇所が多い。哀しいことだが、逆にいうと、基本的な数学もわからないのに、よくもまあ読もうという気になったものだ、ちょっとしたドン・キホーテだ。

データ解析 - 読了："Small Area Estimation"

« 2018年6月 | メイン | 2018年8月 »

rebuilt: 2020年11月16日 22:39
validate this page