« 読了:Muthen & Satorra (1995) 複雑な標本抽出デザインのデータに対するSEM | メイン | 読了:Pearl (2014) シンプソン・パラドクスよ、お前はもう解けている »
2014年3月18日 (火)
2015/06/10 追記: 一年以上前に書いたこの記事を自分で読み返していたら、シミュレーションのコードは汚いわ、結果を読み違えているわで、いやあ、こっぱずかしい... 以下、書き直しました。
Spencer, D. (2000) An approximate design effect for unequal weighting when measurements may correlate with selection probabilities. Survey Methodology, 26(2), 137-138.
最近読んだ何本かの論文で引用されていたので、ついでに目を通した。
抽出確率が不均一な調査デザインのデータにおいては、バイアスを取り除くために集計の際に確率ウェイティングを行うことがあるが、その副作用として母集団パラメータの推定精度が低下する。この推定精度の低下を、推定量の分散と「単純無作為抽出の場合における推定量の分散」との比で表してデザイン効果と呼ぶ。
Kishの有名な近似式によれば、母平均推測における層別抽出のデザイン効果は、ウェイト値の相対分散を$rvw$として$1+rvw$である。しかし、Kishの近似式は抽出確率と無関連な変数の集計を想定している。抽出確率と関連している変数については、推定精度はむしろ向上する場合さえある。そういう場合の近似式をご提案します、という短い報告。
母集団サイズを$N$とする。ケースをひとつ抽出したときそれがケース$i$である確率を$P_i$とする。当然、母集団を通した$P_i$の平均は$1/N$になる。ケース$i$の測定値を$y_i$とする。
いま、母集団において回帰式
$y_i = \alpha + \beta P_i + \epsilon_i$
が成り立っているとしよう。
以下、母分散を$\sigma^2$, 母相関を$\rho$で表す。原文ではそのあとに添え字がついているけど($\sigma^2_y$とか)、わかりにくいのでかっこに入れて示す($\sigma^2[y]$とする)。
サンプルサイズ$n$の標本について考える。以下ではウェイトを、(抽出確率)*(標本サイズ)の逆数、すなわち$w_i = 1/(n P_i)$と表現する。
母集団合計$Y$の推定について考える。推定量は
$\hat{Y} = \sum^n_i w_i y_i$
その分散は
$V(\hat{Y}) = (1/n) \sum^N_i P_i (y_i / P_i - Y)^2$
ここにさっきの回帰式を放り込むと下式となる由。母集団を通じた$w_i$の平均を$\bar{W}$として、
$V(\hat{y})$
$= \alpha^2 N(\bar{W}-N/n)$
$+ (1-\rho^2[y, P]) \sigma^2[y] N \bar{W}$
$+ N \rho[\epsilon^2, w] \sigma[\epsilon^2] \sigma[w]$
$+ 2 \alpha N \rho[\epsilon, w] \sigma[\epsilon] \sigma[w]$
導出過程を追いかけてないけど、信じますよ、先生。
さて、さきほどの回帰式が測定値$y_i$と抽出確率$P_i$ の関係をうまく捉えているならば、それがどんな関係であろうが(関係があろうがなかろうが)、残差項とウェイトは無相関である。すると、上式の$\rho[\epsilon^2, w], \rho_[\epsilon, w]$が$0$になるから、
$V(\hat{y}) = \alpha^2 N(\bar{W}-N/n) + (1-\rho^2[y, P]) \sigma^2[y] N \bar{W}$
いっぽう、単純無作為抽出の場合の分散は (話を簡単にするために復元抽出だとして)
$V(\hat{y}) = (1/n) N^2 \sigma^2[y]$
この比をとったのがデザイン効果だ。すなわち
$deff = (\alpha/\sigma[y])^2 (n \bar{W} / N - 1) + (1-\rho^2[y, P]) n \bar{W} / N$
このデザイン効果の推定値は、結局
$(\hat\alpha/\hat\sigma[y])^2 (rvw) + (1-\hat\rho^2[y, P]) (1+rvw)$
となる由。Kishが想定した$y$と$P$が無相関な状況では、$\hat\alpha$も$0$に近くなるから、結局
$1 + rvw$
となるわけで、つじつまが合っている。
...という主旨の論文であった。
へー、そうなの?と思って、ちょっと実験してみた。
母集団が5つの層から構成されていると考える。層の構成比は1:2:3:4:5とする。各層の母平均をいろいろ操作し、次の3つを比較した。
- 単純無作為抽出による母平均の推測。
- 各層のサンプルサイズを層の構成比に比例させた層別抽出による母平均の推測。
- 各層のサンプルサイズを等しくした層別抽出による母平均の推測と、Spencerのデザイン効果の推測(Kishのデザイン効果は母平均がどうであろうが1.222となる)。
サンプルサイズは100。測定値は(母平均)+(SD1の正規ノイズ)として生成した。試行数5万のモンテカルロ・シミュレーション。シミュレーションのRコードはこちらにございます。コーディングが下手なのはお慰みで。
結果はこうなりました。クリックで拡大表示されるはず。
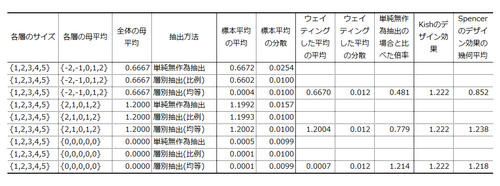
シナリオ1. Spencerのデザイン効果の活躍が期待される状況。各層の母平均を{-2,-1,0,+1,+2}とし、全体の母平均(0.6667)を推測した。単純無作為抽出による標本平均は分散0.0254。これに対し、層別抽出(比例)による標本平均は分散0.0100。層別抽出(均等)による母平均の推定値(つまりウェイティングした平均)は分散0.0122。単純無作為抽出に比べて分散が0.481倍に激減している。層が測定値と抽出確率の両方と強く関連しているので、層別抽出が猛烈な威力を発揮したわけだ。
層別抽出の毎試行ごとにSpencerのデザイン効果を算出してみると、その幾何平均は0.852であった。Kishのデザイン効果(1.222)は推定量の分散の減少を捉えることができないが、Spencerのデザイン効果も減少の大きさを捉えきれていない。なぜだろう?
シナリオ2. Spencerくんの手にも負えないであろう状況。各層の母平均を{+2,+1,0,+1,+2}としてみる(全体の母平均は1.2)。単純無作為抽出では、標本平均の分散は0.0157。層別抽出(比例)では分散0.0100。層別抽出(均等)では分散0.0122。単純無作為抽出に比べて分散が0.779倍に減少している。さきほどと同様、層別抽出にしておいてよかった、というケースである。
Spencerのデザイン効果の幾何平均は1.2380。Kishのデザイン効果はもちろんSpencerのデザイン効果も、標準誤差の減少を捉えられない。測定値と抽出確率のあいだに強い関係があるのだが、それが非線形であるためだろう。
シナリオ3. Kish先生のやり方でよさそうな状況。各層の母平均を{0,0,0,0,0}としてみた(全体の母平均はもちろん0)。単純無作為抽出では、標本平均の平均は分散は0.0099。層別抽出(比例)では分散0.0100。層別抽出(均等)では分散0.0120。要りもしないウェイティングをしたせいで、標準誤差が1.214倍に拡大してしまったわけだ。
Spencerのデザイン効果の幾何平均は1.218であった。この状況なら、Kishのデザイン効果(1.222)もSpencerのデザイン効果も、まあまああたっている。
うーむ。シナリオ 1 における推定量の分散の減少を捉えきれないとすると、Spencerの近似式が役に立つのは一体どういうときなのか、いまいちわからなくなってきた。
論文:データ解析(-2014) - 読了:Spencer(2000) 抽出確率が測定値と相関している標本におけるデザイン効果の推測