« 2019年10月 | メイン | 2019年12月 »
2019年11月28日 (木)
しばらく前に、$n$個の二値変数の同時分布を少数のパラメータでうまく表現しなければならない、という用事があり、さんざっぱら悩む羽目になった。地べたを這いずり回るような仕事をしているもので、時々そういう変な用事が出現するのである。なんかさあ!AIがどうとかさあ!ディープラーニングがどうとかさあ!そういう華やかな仕事をしたいもんだよね! (嘘です。仕事せず寝ているのが理想だ)
この話題、専門の方には簡単なんだろうけど、私にはかなり難しくて、途中でかなりの混乱に陥った。恥ずかしながら当初は、多変量正規分布と同じパラメータ数があれば十分だろう、つまり、周辺割合が$n$個、2変数間の連関を表すパラメータが$n(n-1)/2$個あれば十分だろう、と思い込んでいたのである。なんとなく多次元IRTやカテゴリカル因子分析モデルが頭にあって、個々の二値変数の背後に正規潜在変数があるというのを自明視していたような気がする。いやー、おかげでずいぶん回り道をした。
冷静に考えると、必要なパラメータ数は$2^n-1$個である。なぜ多変量正規分布よりもパラメータ数が増える??とまたまた混乱したのだが、お世話になっている先生に意外な角度からのアドバイスを頂いたりして(さすがプロの研究者はちがう...)、数日かけて頭を冷やし、素人ながらもなんとなく腑に落ちてきた。普段あまり意識していなかったけど、多変量正規性というのは結構きつい制約なんですね。反省。
というわけで、個人的には学ぶところ多かったが、これを考える事情をもたらした案件のほうは中止になってしまい、私の苦闘は丸ごと無駄に終わった。どうもそういう人生みたいだ。
Teugels, J.L. (1990) Some representation of the multivariate bernoulli and binomial distributions. Journal of Multivariate Analysis. 32(2), 256-268.
上記の都合により、勉強のつもりで読んだ論文。
多変量ベルヌーイ分布、つまり複数のベルヌーイ変数の分布について考える。
まずは2変数の場合について考えよう。以下、$p_{00}=P(X_1 = 0, X_2 = 0)$という風に書くことにする。
2変数の場合のパラメータは3つである。その3つは、$p_{00}, p_{10}, p_{01}, p_{11}$のうちどれか3つだと考えてもいいし(当然ながら4つの和は1だから)、ふたつの周辺分布$p_1 = E(X_1) = P(X_1 = 1), p_2$と、$\sigma_{12} = E(X_1-p_1)(X_2-p_2)$の計3個だ、と考えてもいい。
[ちょっとわかりにくいけど、$p_{00}$の添字は値を示し、$p_1$や$\sigma_{12}$の添字は変数番号を示している]
$q_1 = 1-p_1$という風に書くとして、
$p_{00} = q_1 q_2 + \sigma_{12}$
$p_{10} = p_1 q_2 - \sigma_{12}$
$p_{01} = q_1 p_2 - \sigma_{12}$
$p_{11} = p_1 p_2 + \sigma_{12}$
と書ける。行列だと、$\mathbf{p}^{(2)} = [p_{00}, p_{10}, p_{01}, p_{11}]^T$として、
$\displaystyle \mathbf{p}^{(2)} = \left[\begin{array}{cc} q_2 & -1 \\ p_2 & 1 \end{array} \right] \otimes \left[\begin{array}{cc} q_1 & -1 \\ p_1 & 1 \end{array} \right] \left[\begin{array}{c} 1 \\ 0 \\ 0 \\ \sigma_{12} \end{array}\right]$
と書ける。
[ええええ? という感じだけど... $\otimes$はクロネッカー積を表していて、この例だと、右側の行列に$q_2$を掛けたのを左上、$-1$を掛けたのを右上、$p_2$を掛けたのを左下、$1$を掛けたのを右下においた4x4の行列ができる。その右から掛けている縦ベクトルは2行目と3行目が0だから、この行列の2列目と3列目は無視するとして、1列目は上から$q_1 q_2, p_1 q_2, q_1 p_2, p_1 p_2$になるし、4列目は上から$1, -1, -1, 1$になるから、なるほど、行列にする前と比べてつじつまが合っている]
あるいは、$\sigma_{12}$のかわりに$\mu_{12} = E X_1 X_2 = \sigma_{12}+p_1 p_2 = p_{11}$を使ってもよい。このとき、
$p_{00} = 1-p_1-p_2+\mu_{12}$
$p_{10} = p_1 -\mu_{12}$
$p_{01} = p_2 - \mu_{12}$
$p_{11} = \mu_{12}$
と書ける。[こっちのほうがなんとなく親しみがわきますね]
行列だと
$\displaystyle \mathbf{p}^{(2)} = \left[\begin{array}{cc} 1 & -1 \\ 0 & 1 \end{array} \right] \otimes \left[\begin{array}{cc} 1 & -1 \\ 0 & 1 \end{array} \right] \left[\begin{array}{c} 1 \\ p_1 \\ p_2 \\ \mu_{12} \end{array}\right]$
となる。[ああ... クロネッカー積というのを持ち出してきた理由がやっとわかった]
3変数に拡張してみよう。
新たに$\theta = E(X_1 - p_1)(X_2 - p_2)(X_3 - p_3)$を導入する。パラメータは$p_1,p_2,p_3,\sigma_{12},\sigma_{13},\sigma_{23},\theta$の7つになり、行列で書くと
$\mathbf{p}^{(3)} = \left[\begin{array}{cc} q_3 & -1 \\ p_3 & 1 \end{array} \right] \otimes \left[\begin{array}{cc} q_2 & -1 \\ p_2 & 1 \end{array} \right] \otimes \left[\begin{array}{cc} q_1 & -1 \\ p_1 & 1 \end{array} \right] \left[ \begin{array}{c} 1 \\ 0 \\ 0 \\ \sigma_{12} \\ 0 \\ \sigma_{13} \\ \sigma_{23} \\ \theta \end{array} \right]$
となる。
[なんだか騙されたような気分だ... なんでこういう風になるのか、いまいち腑に落ちないんだけど、とにかく先に進もう]
$\mathbf{p}^{(n)}$へと一般化しよう。
$\mathbf{p}^{(n)}$は長さ$2^n$のベクトルである。いま、$k_i \in \{0,1\}$として、$(k_1, k_2, \ldots, k_n)$と一対一に対応するbinary expansion形式の変数
$k = 1 + \sum_{i=1}^{n} k_i 2^{i-1}$
を考えよう。$p_{k_1,k_2,\ldots,k_n}$ は$p_k^{(n)}$と書きかえられる。
[なにをほざいておるのかというと、$(k_1, k_2, \ldots, k_n)$に順に$1, 2, 4, 8, \ldots$という重みを振った加重和に1を足して$k$と呼びましょうということである。要するに、$\mathbf{p}^{(n)}$の要素番号を$k$としましょうってことね]
以下では$Y_i = 1-X_i$と書く。[原文では$\bar{X}_i$なんだけど、わかりにくいので勝手に書き換えた]
以下のように書ける。
$p_k^{(n)} = P(\cap_{i=1}^n [X_i = k_i]) = E(\prod_{i=1}^n X_i^{k_i} Y_i^{1-k_i})$
さて、一般に$2 \times 1$ベクトルのクロネッカー積は次の性質を持つ:
$\left[ \left[ \begin{array}{c} a_n \\ b_n \end{array} \right] \otimes \left[ \begin{array}{c} a_{n-1} \\ b_{n-1} \end{array} \right] \otimes \cdots \otimes \left[ \begin{array}{c} a_1 \\ b_1 \end{array} \right] \right]_{k} = \prod_{i=1}^n a_i^{1-k_i} b_i^{k_i}, \ \ 1 < k < 2^n$
[なにをぬかしておるのかというと、たとえば$n=2$のとき、
$\left[ \begin{array}{c} a_2 \\ b_2 \end{array} \right] \otimes \left[ \begin{array}{c} a_1 \\ b_1 \end{array} \right] = \left[ \begin{array}{c} a_2 a_1 \\ a_2 b_1 \\ b_2 a_1 \\ b_2 b_2 \end{array} \right]$
だよね? で、たとえば$k=2$(つまり$k_1=1, k_2=0$)番目の要素をみると、これは$a_1^{1-k_1} b_1^{k_1} \times a_2^{1-k_2} b_2^{k_2}=a_1^0 b_1^1 \times a_2^1 b_2^0$だよね? つまり、クロネッカー積の$k$番目の値がほしかったら、その$k$を$(k_1, k_2, \ldots, k_n)$に戻し、$i=1, \ldots, n$について、$k_i$が0だったら$a_i$, $1$だったら$b_i$を拾ってきて掛ければいいんだよ、ということであろう。そういわれればそうなんだけど、よくもまあ、こんな難しい書き方を...]
$a_i = Y_i, b_i = X_i$とすると、
$\mathbf{p}^{(n)} = E \left( \left[ \begin{array}{c} Y_n \\ X_n \end{array} \right] \otimes \left[ \begin{array}{c} Y_{n-1} \\ X_{n-1} \end{array} \right] \otimes \cdots \otimes \left[ \begin{array}{c} Y_1 \\ X_1 \end{array} \right] \right)$
となる。
さて。$\mathbf{\mu}^{(n)}$, $\mathbf{\sigma}^{n}$を次のように定義する。それぞれの$k$番目の要素について、
$\mu_k^{(n)} = E \left( \prod_{i=1}^{n} X_i^{k_i} \right) = E \left( \left[ \begin{array}{c} 1 \\ X_n \end{array} \right] \otimes \left[ \begin{array}{c} 1 \\ X_{n-1} \end{array} \right] \otimes \cdots \otimes \left[ \begin{array}{c} 1 \\ X_1 \end{array} \right] \right)_k$
$\sigma_k^{(n)} = E \left( \prod_{i=1}^{n} (X_i-p_i)^{k_i} \right) = E \left( \left[ \begin{array}{c} 1 \\ Y_n \end{array} \right] \otimes \left[ \begin{array}{c} 1 \\ Y_{n-1} \end{array} \right] \otimes \cdots \otimes \left[ \begin{array}{c} 1 \\ Y_1 \end{array} \right] \right)_k$
[ぴんとこないので$n=2, k=4$(つまり$k_1 = 1, k_2=1$)について考えると、
$\mu_4^{(2)} = E( X_1^{k_1} X_2^{k_2} ) = E( X_1 X_2 ) $
つまりこれは最初の練習に出てきた$\mu_{12}$である。
$\sigma_4^{(2)} = E ( (X_1-p_1)^{k_1} (X_2-p_2)^{k_2} ) = E (X_1-p_1)(X_2-p_2)$
つまりこれは最初の練習に出てきた$\sigma_{12}$である。はいはい]
以下の定理を得ることができます。[証明は省略する。すいません、私ただのしがない労働者ですもんで]
定理1-1.
$\mathbf{p}^{(n)} = \left[ \begin{array}{cc} 1 & -1 \\ 0 & 1 \end{array} \right]^{\otimes n} \mathbf{\mu}^{(n)}$
かつ
$\mathbf{\mu}^{(n)} = \left[ \begin{array}{cc} 1 & 1 \\ 0 & 1 \end{array} \right]^{\otimes n} \mathbf{p}^{(n)}$
パラメータ数は$2^n-1$個となる。$\mathbf{\mu}^{(n)}$の長さは$2^n$だが、$\mu_1^{(n)}=1$だから。
定理1-2.
$\mathbf{p}^{(n)} = \left[ \begin{array}{cc} q_n & -1 \\ p_n & 1 \end{array} \right] \otimes \left[ \begin{array}{cc} q_{n-1} & -1 \\ p_{n-1} & 1 \end{array} \right] \otimes \cdots \otimes \left[ \begin{array}{cc} q_1 & -1 \\ p_1 & 1 \end{array} \right] \mathbf{\sigma}^{(n)}$
かつ
$\mathbf{\sigma}^{(n)} = \left[ \begin{array}{cc} 1 & 1 \\ -p_n & q_n \end{array} \right] \otimes \left[ \begin{array}{cc} 1 & 1 \\ -p_{n-1} & q_{n-1} \end{array} \right] \otimes \cdots \otimes \left[ \begin{array}{cc} 1 & 1 \\ -p_1 & q_1 \end{array} \right] \mathbf{p}^{(n)}$
パラメータ数はどうなるか。$\mathbf{\sigma}^{(n)}$の長さは$2^n$だが、$k_1 + k_2 + \cdots + k_n = 1$の箇所は0になるから、$2^n -n - 1$個。これが依存性を表しているわけだ。これに加えて$p_i$が$n$個あるから、結局パラメータ数は$2^n-1$である。[あー!なるほどねえ!]
[ここからは、多変量ベルヌーイ分布の確率母関数の導出。メモは省略]
なお、分割表の分析には対数線型モデルが使われることも多い。たとえば$n=3$の飽和モデルは、クロネッカー積を使えば次のように書ける。$v_{ijk} = \log p_{ijk}$のベクトルを$\mathbf{v}^{(3)}$として、
$\mathbf{v}^{(3)} = \left[ \begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array} \right]^{\otimes 3} \mathbf{\lambda}^{(3)}$
ただし$\mathbf{\lambda}^{(3)} = (\mu, \lambda_1, \lambda_2, \lambda_{12}, \lambda_3, \lambda_{13}, 0, \phi)^T$。
[ほんまかいな? というわけで、展開してみると...
$\left[\begin{array}{c} v_{000} \\ v_{100} \\ v_{010} \\ v_{110} \\ v_{001} \\ v_{101} \\ v_{011} \\ v_{111} \end{array} \right] = \left[ \begin{array}{cccccccc} +1 & +1 & +1 & +1 & +1 & +1 & +1 & +1 \\ +1 & -1 & +1 & -1 & +1 & -1 & +1 & -1 \\ +1 & +1 & -1 & -1 & +1 & +1 & -1 & -1 \\ +1 & -1 & -1 & +1 & +1 & -1 & -1 & +1 \\ +1 & +1 & +1 & +1 & -1 & -1 & -1 & -1 \\ +1 & -1 & +1 & -1 & -1 & +1 & -1 & +1 \\ +1 & +1 & -1 & -1 & -1 & -1 & +1 & +1 \\ +1 & -1 & -1 & +1 & -1 & +1 & +1 & -1 \end{array} \right] \left[ \begin{array}{c} \mu \\ \lambda_1 \\ \lambda_2 \\ \lambda_{12} \\ \lambda_3 \\ \lambda_{13} \\ 0 \\ \phi \end{array} \right]$
右辺左側の正方行列は、1列目から順に、全平均、要因$i$の主効果、$j$の主効果, $i \times j$の交互作用効果、$k$の効果、$i \times k$の交互作用効果、$j \times k$の交互作用効果、$i \times j \times k$の二次交互作用効果になっている(というか、L8直交表の左に1の列を付け加えた形になっている)]
これを最初で示した例と見比べると、パラメータ数はどちらも7だけど、解釈が異なる。
我々の$\mathbf{p}^{(n)} = A_n \mathbf{\sigma}^{(n)}$という書き方だと、$\theta=0$とすることなく$\sigma_{12} = \sigma_{13} = \sigma_{23} = 0$とおける。つまり、対数線型モデルのように階層的構造を考える必要がない。
さらに、我々の定式化だと、ひとつ以上の$p_{ijk}$が0であってもなんの問題もない。対数線型モデルでは結構難しくなる。
云々...
... ここまでが論文の前半。後半は多変量二項分布の話になり、いま関心ないのでパス。
習わぬお経を無理矢理読むようなつもりでメモをとったが、それなりに勉強になった。クロネッカー積を使うとこんなに綺麗に書ける、っていうところに感心した。世の中には頭のいい奴がいるものだ。
論文:データ解析(2018-) - 読了:Teugels (1990) 多変量ベルヌーイ分布をどうやって表現するか
2019年11月15日 (金)
用事があって、日帰りで長野の軽井沢というところに行った。有名な避暑地だが、これまでご縁がなく、記憶の限りでは初めての訪問である。
思ったより早く帰れることになったのだが、夕方の軽井沢駅は池袋駅並みにごった返しており、切符の都合で1時間半ほど時間を潰さなければならなくなった。駅の北側に少し歩いて、運よく喫茶店に空席をみつけた。
本でも読もうと思ったんだけど、ウェイターのお兄さんがコーヒーと一緒になにかをテーブルに置き、「時間つぶしにでもどうぞ...」という。それは木製の小さなパズルであった。ボードの上にイラストが描かれた小さなコマがいくつかあり、使い込まれてかすかに茶色い光沢を帯びている。コマを上下左右にずらし、目指す模様をつくるパズルだ。子供の頃にやったことがある。
「ははは」と愛想笑いしたけれど、そんなに暇そうに見えたかなあ、とちょっと気になった。もっともこれは私の気の回しすぎで、他のテーブルのお客さんにも渡していたようである。隣のテーブルの母娘連れも、親戚の悪口などを云いながらひとしきりこのパズルで遊んでいた。
鞄から本を取り出したが、こんな子供だましのパズルも懐かしいものだ、などと思い、頬杖をつき、戯れに指でコマを適当に滑らせてみた。完成したら本でも読もうか、と。
... それから1時間半。読書どころか、ぶっつづけでこのパズルに取り組む羽目になった。
解けない!解けないよ!
このパズル、めちゃくちゃ難しいじゃん!!
時間切れでお店を出るときにはイライラが極限に達しており、レジの横に並べられたこのパズルをひっつかんで買ってしまった。1300円、思わぬ出費である。店主らしき方が笑っていた。
帰りの新幹線でもこのパズルがぐるぐると頭をめぐって離れなかったのだが(「あの4つのリンゴを隣り合わせにして...」云々)、いやまてよ、と我に返った。レジ前の陳列には「日本一難しいパズル」と謳われていた。このパズル、たぶんほんとに難しい奴なのだ。いっぽう、私はあんまし頭の良いほうじゃない。パズルなんて大の苦手だ。なにも私が頑張って解くことはないんじゃないか。
むしろ、パズルを解くプログラムを書いたほうが早いんじゃないか?
問題
買ってきたパズルはこちら。
 コマをボードの外に出さずに移動させ、左上のこびとを右下の角に3つの柵でとじこめる、というのがゴールである。
コマをボードの外に出さずに移動させ、左上のこびとを右下の角に3つの柵でとじこめる、というのがゴールである。パズルももちろん著作物であり、勝手にブログに載せてはいけないと思ったのだが、検索してみたところ、喫茶店の方が画像を公開しておられることに気が付いた。これって、喫茶店の店主の方のオリジナル作品なのかしらん? すごいなあ。
お店の名前は「喫茶館丹念亭」。とてもよい雰囲気のお店で、コーヒーもシナモンケーキも美味しかった。いつかまた軽井沢に行く機会があったら立ち寄りたいと思います。
うちに帰ってビールを飲みながら再び試してみて、このパズルにはまった理由がなんとなくわかってきたような気がした。
このパズル、なんとなくコマをすべらせていると、なんとなく盤面が変化する。思いもよらぬ形で大きなコマが動いたときなど、ちょっとした快感がある。しかしよくみると、全く展望が開けていない。同じような局面をぐるぐると回っているだけで、そこから全く脱出できないのである。まるで迷路にはまり込んでしまったような気分だ。
よくわからんが、こういうパズルを考案するのってきっとすごい才能と努力の結晶なのであろうと思う。ほんとに尊敬します。
プログラムで解くにあたっての方針は次の通り。
- Rで書く。この課題にRが向いているからではなくて、単に私がRに慣れているからである。
- このパズルに限らず、このタイプのパズルすべてに適用できるプログラムにする。Wikipediaによれば、こういうパズルのことをスライディング・ブロック・パズル、ないしスライド・パズルと呼ぶらしい。知らなかった。
- 初期状態(つまり、最初のコマの配置)から出発し、そこからコマを動かして到達し得る状態を、力づくですべて探索する。なぜなら、どういう評価関数を書いたらいいのか、私にはよくわからんからである。
- 得られたすべての状態からなるネットワーク・グラフを生成する。パズルの解を求めるコードは書かない。だって、グラフが手に入っていれば、ネットワーク分析のソフトを使えば最短経路を探索できるじゃん?
- 朝までに書き終える。
我ながら頭の悪さがにじみ出る方針である。特に最後の奴がそうだ。結局、翌朝までには書けませんでした。
上で状態のネットワーク・グラフと書いたが、これはこういう意図である。
このパズルについていえば、最初にできるのは右上の柵を上に動かすことだけである。2手目にできることは2つある。右端列の下から2番目のリンゴを上に動かす、ないし、右から2つめのリンゴ2個のピースを上に動かしていくことである。3手目にできることは...
... と考えていくと、どんどん枝分かれしていくが、単純に増えていくだけではない。元の状態に戻ったり、別の手順でたどり着いた状態に一致したりすることもありうる。
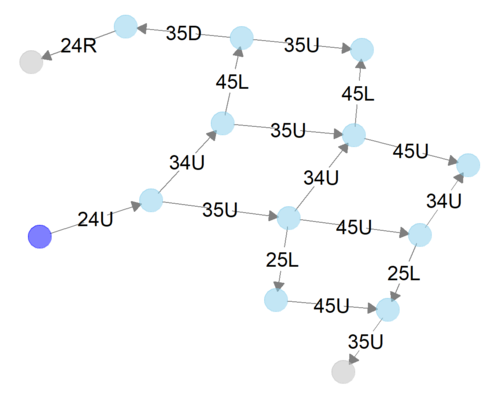
上図は5手までの状態を表現するネットワーク・グラフである。紫色のノード(円)は初期状態を表している。24Uとは「行2, 列4にあるコマを上に動かす」こと、つまり右上の柵を上に動かすことを意味している。
このように、5手までで14個の状態に到達できるわけだ。到達できる状態の数はどんどん増えていく。これをずーっと続けていけばさ!いつかはゴールに辿りつくよね!
後述するが、こういう過度に楽観的な態度、問題の難しさを最初に客観的に推し量ることを怠る姿勢が、人生の悲劇を招くのである。
これがパズルの解答だ
初期状態から到達し得る状態をすべて調べてみた。ただし、目標条件を満たす状態に辿り着いたら、そこからさらに探索するのはなし、ということにした。つまり、何も考えずにピースを動かしてはいるものの、ゴールに辿り着いたことに気がつかないほどアホではないプレイヤーが、いったいどのような盤面に辿り着きうるか、網羅的に調べたわけである。
軽井沢で買ったパズルの場合、手元のパソコンで約8時間で探索が終了した。8時間。映画を4本見られる時間、本を数冊読める時間、精力絶倫な王様なら子供をたくさん作れる時間だ。
すべての状態のネットワーク・グラフを描いてみた。それではご覧ください。軽井沢駅北口の喫茶店の店内でパズルのコマを動かしているみなさん! あなたはいま、この図の中のどこかにいますよ!
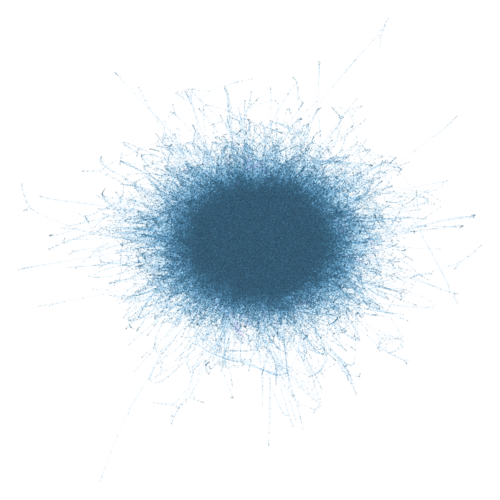
ネットワーク・グラフどころか、なにか模様のようなものしかみえないが、これはカメラをすごく引いているからで、目を凝らせば見えるであろう微小な点が個々の状態を表している。状態の数は977,412個。うち1個は初期状態、14個はゴールの条件を満たす状態である。
これではあまりに見にくいので、初期状態からゴールまでの経路(正確に言うと、14個のゴールそれぞれへの最短経路)の途中に位置する状態、計3,028個だけを抜き出して描いてみると...

青いノードが初期状態、ピンクのノードが経路上の状態、赤いノードがゴール状態である。
青いノードをお探しですか? 図右側のちょっと下寄りにあります。拡大してみましょう。
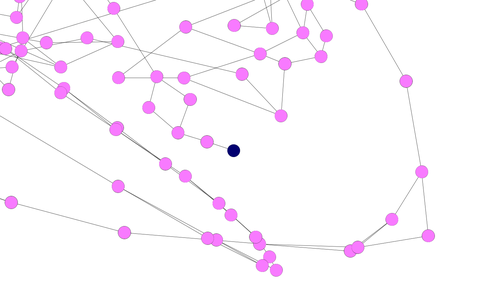
要は、この青いノードから辿って行けば、誰でもゴールにたどり着けるわけだ。
ああよかった、これで自分でパズルを解く必要がなくなった。夜もぐっすり眠れるというものだ。
ついでにいうと... 野暮なのでパズルの解答は書きませんけど、このパズルにおけるゴールへの最短経路は217手である。
買ってきたパズルには親切にも模範解答を図示した紙が添付されているのだが、その手数は254手(181手と記載されているが、ここではひとつのコマの1マスの移動を1手と数える)。おかげさまで、模範解答よりもすこし手数の少ない解答を見つけたことになる。ほんの少しだけ達成感があるが、いやいやそれよか、パズルを考案する人のほうがずっとすごいですよね。
だからどうした
だからどうしたんだこの暇人め、といわれると困ってしまうのだが、今回は自分なりにいろいろ学ぶところ大きかった。
帰りの新幹線のなかでぼんやり思ったのは、どうせ盤面の状態は限られているだろう、ということであった。盤面の大きさは4x5マス、コマの数は10個。喫茶店内でコマをあれこれ動かしているときも、なんだか同じ状態を行きつ戻りつしているような気がしてならなかった。だったら私にも全探索できちゃうんじゃない?と思ったのである。
振り返るとこれは無謀な賭けであった。組み合わせの数の大きさというものは人間の直感を遥かに超える。今回のパズルはたまたま初期状態から到達できる状態の全探索が可能であったし、あとで試算したところでは、そもそもこのパズルで可能な状態の数は1,281,550個しかない。しかし、問題が少し異なるだけで、状態の数は爆発的に増大し、まともな時間では到底全探索できないものとなっていただろう。
なんについてもいえることなんだろうけど、最初に問題の大きさを推し量ることって、すごく大事ですね。どうもそういう姿勢が私には欠けているようだ。反省。
なぜ難しいのか
それにしても不思議なのは、このパズルがなぜこんなに難しいのかという点である。実際に遊んだことがない方に、解のネタバレを避けつつ説明するのはすごく難しいんですが、とにかくほんとに難しいんですってば。イライラするんですってば。
難しい理由のひとつは、もちろん、ゴールまでの手順の多さであろう。しかしそれだけが要因ではないという気がしてならない。なんというか、いくらコマを動かしても、同じような局面をぐるぐると回っているように感じられるのである。
こうした難しさを、ネットワーク・グラフの形状によって定量的に示すことはできないだろうか。
同じような局面からなかなか脱出できないということは、ネットワーク・グラフのあちこちにノードの密な固まりがあって、その固まりから外に出て行くエッジが少ない、ということだろう。とすれば、ネットワーク・グラフ全体を通じてノードが局所的に固まっている程度を測ればよいのではないか。このパズルでは、その値がとても高くなっているのではないか?
思い悩んだ末、次のようなことを試してみた。
あるネットワーク・グラフについて、ノードをいくつかのグループにわけたとする。ネットワーク分析の慣例に従い、これをコミュニティと呼ぶことにする。
ノードの間のエッジは、同一コミュニティ内でつながるエッジと、コミュニティをまたがるエッジとにわかれる。前者のエッジの比率が大きいとき、コミュニティはネットワークのなかの密度の高い固まりをうまく捉えていることになる。
そこで、コミュニティ内のエッジの比率が、「そのグラフのエッジを一旦すべて消し、かわりに同じ数のエッジをランダムに張ったときに得られる、コミュニティ内のエッジの比率」と比べてどれだけ大きいかを調べる。これをモジュラリティという。うーん、下手な説明だが、要するに、モジュラリティが大きいことは、ノードがコミュニティの中で高密度に固まっていることを示しているわけである。
上のアイデアに従い、丹念亭パズルのネットワーク・グラフを徐々にたくさんのコミュニティに分割していき、そのたびにモジュラリティを測ってみよう。
どうやってコミュニティに分割するか。いろんな方法があるんだけど、ここでは手っ取り早く、Clausetたちの手法を使うことにする。これ、計算がすごく速いんです。
比較のために、すごくシンプルなスライドパズルについても同じことを試してみる。盤面は3x3, コマは8つ、サイズはすべて1x1であるパズルを考える。つまり、下図を3x3に縮めたようなパズルです。
このパズルについて、初期状態から辿り着くことができるすべての状態(181,440個)のネットワーク・グラフを作った。で、こちらについてもコミュニティ数を増やしながらモジュラリティを調べた。
結果は下図の通り。
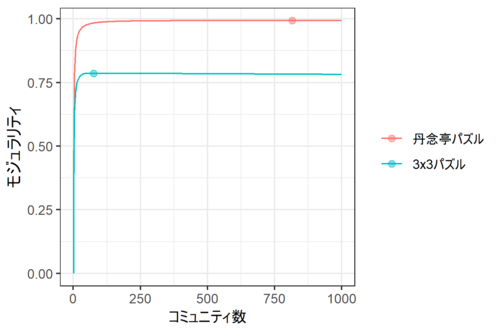
丹念亭のパズルではコミュニティ数816、3x3のパズルではコミュニティ数76のとき、モジュラリティが最大になった。
ここで注目したいのはモジュラリティの違いである。丹念亭パズルのモジュラリティは最大で0.993と、法外に高い。つまり、ネットワーク・グラフの描画からは読み取れないが、あたかも少量の水に溶かした小麦粉のダマのように、ノードが小さくて密度の高い固まりを形成しているのではないかと思う。そのため、やみくもにコマを動かしても、その固まりの外側になかなか出られない... ということではないかしらん?
疑問点
... などと書いてはみたものの、正直なところ、あまり自信がない。
- 3x3パズルは丹念亭のパズルよりも状態数が小さいし(9!=362880通り)、ネットワーク・グラフの作成にあたって目標状態を設定せずに全探索しているので、適切な比較になっているかどうかわからない。
- Clausetたちの手法は凝集的なコミュニティ検出手法なので、所与のコミュニティ数についてモジュラリティ最大のコミュニティを検出していないかもしれない。
- なにより、ここでモジュラリティに注目したのは良いやり方だったのだろうか。ネットワークがクラスタ化している程度を調べる際にはクラスタ係数と呼ばれる指標を使うことが多いと思うんだけど、スライド・パズルの状態のネットワーク・グラフはクリークを持たないので(3手で元に戻ることはできないから)、クラスタ係数は0となる。こういうネットワークについて、それがクラスタ化されている程度を調べるためにはどうしたらいいんだろう?
ううむ... このへんで時間切れということにしておくけど、いろいろ勉強が足りないことがわかった。
rSlidePzlパッケージ
軽井沢駅前の喫茶店でパズルを渡された副産物として、任意のスライド・パズルについて初期状態から到達しうる状態を全探索しネットワーク・グラフを生成するRパッケージ rSlidePzl を作りました。
ああ、私には聞こえる。任意のスライド・パズルについて初期状態から到達しうる状態を全探索しネットワーク・グラフを生成したいと思っている、世界三千万人の善人男女の歓喜の叫びが。(嘘です聞こえません)
パッケージはgithubからインストールできる。
このパッケージを使えば、お手元のスライド・パズル(9x9マス以内)について、初期状態から到達し得る状態をすべて探索し(幅優先探索)、みつかった状態からなるネットワーク・グラフをつくることができる。
せっかくなので、初期状態からゴールへの最短手順を出力する関数もつくっておいた。また、得られたネットワーク・グラフを(それが小さめであれば)簡単に描画できる関数もつくった。
探索すべきすべての状態を探索し尽くす場合、とんでもなく時間がかかることを覚悟する必要がある。これを避けるため、探索する手の深さ(何手目まで探索するか)や、探索する状態の総数について上限を指定し、探索を途中で打ち切ることもできる。
このパッケージを使って得られるネットワーク・グラフは igraph パッケージの igraph クラスのオブジェクトである。igraph パッケージが提供する多様な関数によって、その性質を心ゆくまで調べることができる。
コード例を示す。
### devtoolパッケージをインストール
### install.packages("devtools")### rSlikePzlパッケージをインストール
# devtools::install_github("shigono/rSlidePzl")### rSlikePzlパッケージをロード
library(rSlidePzl)library(tidyverse)
library(igraph)### セッティング
oSetting <- makeSetting(
## 盤面のサイズ (行サイズ, 列サイズ)
boardsize = c(4,5),
## コマのサイズ (行サイズ, 列サイズ)
piecesize = list(
A = c(2, 2), # コマタイプA.こども パズルに添付されている解答ではNo.1
B = c(2, 1), # コマタイプB.りんごとサク No.5
C = c(1, 2), # コマタイプC.横長のサク No.7
D = c(1, 1), # コマタイプD.りんご, No.2,3,9,10
E = c(2, 1), # コマタイプE.縦長のサク, No.6
F = c(2, 1), # コマタイプF.縦長のりんご No.8
G = c(1, 2) # コマタイプG.横長の林檎 No.4
)
)### こどものピースの位置(1,1), (1,2), (2,1), (2,2)について考える
anNumStates <- sapply(
list(c(1,1), c(1,2), c(2,1), c(2,2)),
function(anLoc){
### 可能な状態の数を算出する
getNumStates(
makeState(
list(
makePiece(type = "A", loc = anLoc),
makePiece(type = "B", loc = c(NA,NA)),
makePiece(type = "C", loc = c(NA,NA)),
makePiece(type = "E", loc = c(NA,NA)),
makePiece(type = "F", loc = c(NA,NA)),
makePiece(type = "G", loc = c(NA,NA))
)
),
oSetting
)
}
)
# - こどものピースが位置(1,1)(左上端)であるときの状態数は、
# 左下端(3,1), 右上端(1,4), 右下端(3,4)にあるときの状態数と同じはずなので、4倍する
# - こどものピースが位置(1,2) にあるときの状態数は、
# (1,3), (3,2), (3,3) にあるときの状態数と同じはずなので、4倍する
# - こどものピースが位置(2,1) にあるときの状態数は、
# (2,4) にあるときの状態数と同じはずなので、2倍する
# - こどものピースが位置(2,2) にあるときの状態数は、
# (2,3) にあるときの状態数と同じはずなので、2倍する
# 各状態においてりんごのピースを置く位置は6 x 5 / 2 通りあるから...
print(sum(anNumStates * c(4,4,2,2)) * 6 * 5 / 2) # 状態数は1281550### 開始時点の盤面の作成
oStart <- makeState(
list(
makePiece(type = "A", loc = c(1,1)), # パズルに添付されている解答ではNo.1
makePiece(type = "B", loc = c(1,3)), # No.5
makePiece(type = "C", loc = c(2,4)), # No.4
makePiece(type = "D", loc = c(3,1)), # No.2
makePiece(type = "D", loc = c(3,2)), # No.3
makePiece(type = "E", loc = c(3,3)), # No.6
makePiece(type = "F", loc = c(3,4)), # No.8
makePiece(type = "D", loc = c(3,5)), # No.9
makePiece(type = "G", loc = c(4,1)), # No.4
makePiece(type = "D", loc = c(4,5)) # No.10
)
)
stopifnot(isValidState(oStart, oSetting))### 目標条件の作成
oGoalCondition <- makeState(
list(
makePiece(type = "A", loc = c(3,4)), # No.1
makePiece(type = "B", loc = c(1,3)), # No.5
makePiece(type = "E", loc = c(3,3)), # No.6
makePiece(type = "C", loc = c(2,4)) # No.7
)
)
stopifnot(isValidState(oGoalCondition, oSetting))### 5手だけ検索
oGraph <- makeGraph(oSetting, oStart, oGoalCondition, verbose = 1, max_depth = 5)### 描画
set.seed(123)
plotGraph(oGraph, method = "GGally")### すべての手順を探索。手元のパソコンで8時間くらい
oGraph <- makeGraph(oSetting, oStart, oGoalCondition, verbose = 1)### 目標条件を満たした状態を表示
print(V(oGraph)[V(oGraph)$status == 4])### 目標条件を満たした状態への最短経路を表示
print(getShortestPath(oGraph)$transition)### コミュニティ検出。fast_greedy法でmodularityを最適化する
oGraph_undirected <- as.undirected(oGraph)
oCommunity <- cluster_fast_greedy(oGraph_undirected, modularity = TRUE)### 描画。Rでは大変なのでGephi (https://gephi.org/) で描く。
### グラフに描画のための属性を追加する
### state_color属性: {1(初期状態),2(目標状態),3(目標への途中),4(ほか)}
### Gephiでこの属性をcolorに指定すると、ノードを色分けできる
anColor <- rep(4, length(V(oGraph))) # 4: 下記以外の状態
anColor[getReachability(oGraph) == 1] <- 3 # 3: 目標状態に至るパス上にある状態
anColor[V(oGraph)[V(oGraph)$status == 4]] <- 2 # 2: 目標状態
anColor[1] <- 1 # 1: 初期状態
V(oGraph)$state_color <- anColor### state_size属性: {1(目標への経路上にない),2(ある)}
### Gephiでこの属性をsizeに指定すると、目標への経路上のノードを大きくできる
V(oGraph)$state_size <- c(2,2,2,1)[anColor]
V(oGraph)$state_comm <- membership(oCommunity)### state_x属性, state_y属性: x座標とy座標
### GephiのGeo layoutでこれらの属性を緯度経度に指定すると、レイアウトを再現できる。
### コミュニティ内のエッジに大きな重みを与え、Fruchterman-Reingoldアルゴリズムで
### 最適化している。Gephiでレイアウトを作成してもいいけど、こっちのほうが速い
oLayout <- layout_with_fr(
oGraph,
weights = ifelse(crossing(oCommunity, oGraph), 1, 10),
niter = 1000
)
### 座標が大きな値だとメルカトル図法では歪んでしまうので、-1から+1に基準化する
oLayout <- norm_coords(oLayout)
V(oGraph)$state_x <- oLayout[,1]
V(oGraph)$state_y <- oLayout[,2]### graphml形式で出力。このファイルをGephiで読み込む
write.graph(oGraph, file = paste0("./full_states.graphml"), format = "graphml")### 3x3パズルのセッティング
oSetting <- makeSetting(
boardsize = c(3,3),
piecesize = list(
A = c(1, 1), B = c(1, 1), C = c(1, 1), D = c(1, 1),
E = c(1, 1), F = c(1, 1), G = c(1, 1), H = c(1, 1)
)
)
oStart <- makeState(
list(
makePiece(type = "A", loc = c(1,1)),
makePiece(type = "B", loc = c(1,2)),
makePiece(type = "C", loc = c(1,3)),
makePiece(type = "D", loc = c(2,1)),
makePiece(type = "E", loc = c(2,2)),
makePiece(type = "F", loc = c(2,3)),
makePiece(type = "G", loc = c(3,1)),
makePiece(type = "H", loc = c(3,2))
)
)
stopifnot(isValidState(oStart, oSetting))### 3x3パズルのネットワーク・グラフ作成
oGraph_Nine <- makeGraph(oSetting, oStart)### 上と同じやり方でコミュニティ検出
oCommunity_Nine <- cluster_fast_greedy(as.undirected(oGraph_Nine), modularity = TRUE)### モジュラリティ比較
oGraph_undirected <- as.undirected(oGraph)
anModularity <- sapply(
1:1000,
function(nNum){
modularity(oGraph_undirected, cut_at(oCommunity, no = nNum))
}
)
oGraph_undirected <- as.undirected(oGraph_Nine)
anModularity_Nine <- sapply(
1:1000,
function(nNum){
modularity(oGraph_undirected, cut_at(oCommunity_Nine, no = nNum))
}
)
dfPlot <- data.frame(
nNumComm = 1:1000,
nMod_1 = anModularity,
nMod_2 = anModularity_Nine
) %>%
gather(sVar, gValue, c(nMod_1, nMod_2)) %>%
separate(sVar, c("sVar1", "nVar2")) %>%
group_by(nVar2) %>%
mutate(bMax = if_else(gValue == max(gValue), 1, 0)) %>%
ungroup() %>%
mutate(fGraph = factor(nVar2, levels = c("1", "2"), labels = c("丹念亭パズル", "3x3パズル")))
g <- ggplot(data = dfPlot, aes(x = nNumComm, y = gValue, color = fGraph))
g <- g + geom_line()
g <- g + geom_point(data = dfPlot %>% filter(bMax == 1), size = 2, alpha = 0.5)
g <- g + labs(x = "コミュニティ数", y = "モジュラリティ")
g <- g + scale_color_discrete(name = NULL)
g <- g + theme_bw()
print(g)### 以上
githubを使うのも、Rパッケージを公開するのもはじめてなので、いろいろ不備があるかもしれませんが、そのへんはひとつ、ご愛敬ということで...
雑記:データ解析 - 軽井沢駅前の喫茶店の店員さんに渡されたパズルを解く (ためのRパッケージを作った)
ふつうのデータ分析のなかで個体のクラスタリングをやるように、ネットワーク・データの分析の際にもノードのクラスタリングをやりたくなることがある。この分野ではクラスタじゃなくてコミュニティと呼ぶことが多いと思うけど。
個体のクラスタリングと同様、コミュニティ検出の方法もいろいろありすぎて、私のような素人は困惑してしまうのだが、中にはやたら時間とメモリを食う奴もあれば、逆に法外に早くできちゃう奴もある。時間がかかる分にはあきらめがつくが、あまりにパッと答えが出ちゃうのは、ありがたいけどなんだか気持ち悪い...という気がする。好き勝手云ってすいません。
Clauset, A., Newman, M.E.J., Moore, C. (2004) Findng community structure in very large networks. arXiv:cond-mat/0408187v2.
というわけで、igraph の cluster_fast_greedy() のドキュメントで引用されていた資料を読んでみた。
Rのigraphパッケージには, コミュニティ検出の手法としてedge betweenness, fast greedy, label prop, leading eigen, louvain, optimal, spinglass, walktrapの8つが載っているが、このうちfast greedyというのは100万ノードくらいあるグラフであっても数分でコミュニティを返してくるので、なんだか気味が悪いのである。お前真面目にやっとんのかといいたくなる。
ノードの隣接行列を$A$とする。ノード$v$と$x$がつながっているかどうかを$A_{vw}$とする。$i=v$のときに1、そうでないときに0になる関数を$\delta(i,j)$とする。グラフのエッジ数を$m=(1/2) \sum_{vw} A_{vw}$とする。
ノード$v$が属するコミュニティを$c_v$とする。エッジのうち、両端が同じコミュニティに落ちている割合は、
$\displaystyle \frac{\sum_{vw} A_{vw} \delta(c_v, c_w)}{\sum_{vw} A_{vw}} = \frac{1}{2m} \sum_{vw}A_{vw} \delta(c_v, v_w)$
となる。この量はネットワークをうまく分割できているときに大きくなるけれど、これ自体はコミュニティ構造の指標にはなれない。すべてのノードが同じコミュニティに属していれば1になるから。
そこで、この量からランダムグラフにおけるこの量の期待値を引く。ノードの次数を$k_v = \sum_w A_{vw}$として、ランダムグラフにおいて$v$と$w$の間にノードがある確率は$k_v k_w/2m$だから、
$\displaystyle Q = \frac{1}{2m} \sum_{vw} \left( A_{vw} - \frac{k_v k_v}{2m} \right) \delta(c_v, c_w)$
これがみなさまご存知の modularity。経験的には、Qが0.3以上のときネットワークには顕著なコミュニティ構造がある。[←へー]
ネットワークのコミュニティへの分割がうまくいっているときmodularityが高いなら、modularityが高くなるような分け方を探せばいいことになる。しかし、すべての分割を通じて大域的に最大のmodularityを探すのは大変なので、なんらか近似的な最適化手法を考えたい。
というわけでですね、かつて我々はNewman(2004)でこういう手法を提案いたしました。まだコミュニティに属していないひとりきりのノードたちからはじめて、Qがもっとも大きくなるような併合を探す。これを$n-1$回繰り返すとついに全員が単一のコミュニティに入ることになる。こうして、ノードを葉としたデンドログラムができる。[←要はあれですかね、F比を評価関数にして凝集型階層クラスタリングをやるようなもんですかね]
さて、この提案の折には、隣接行列を整数の行列として持っておいて毎回行と列をマージしていけばいいや、と思っていた。しかし巨大な疎行列の場合、ほとんどの要素が0なので、この作業は無駄である。
そこで本日はもっと効率的な方法を御提案します。[←ええええ? そういう論文なの?]
... というわけで、いちおう最後までめくったけど、論文の主旨は計算を速くするための工夫の話だったので、メモは省略。よくわからんが、ネットワークの隣接行列を更新するんじゃなくて、ネットワークのコミュニティの隣接行列を更新すればよくね? というような話らしい。
要するに... やっていることは階層的クラスタリングなんだけど、ネットワーク・データの場合は元の距離行列が疎なので、計算をめっちゃ速くするテクニックがあります、ということらしい。ふうん。
論文:データ解析(2018-) - 読了:Clauset, Newman, Moore (2004) すごく大きなネットワークにおけるコミュニティ検出
2019年11月13日 (水)
ここんところこういう覚え書きばかりで、自分でも嫌になっちゃうんだけど...
無向グラフにおいて、ノードiとj, jとkの間にエッジがあるときに、iとkの間にもエッジがあることを推移的であるという。有向グラフでは、iからj, jからkへのエッジがあるときに、iからkへのエッジもあることを推移的であるという。
あるグラフにおいて、推移的であるかもしれない2つのノード(上でいうiとk)が実際に推移的である割合を推移性 transitivity という。えーと、Newman, Watts & Strogatz(2002)が提案したのだそうだ。
Rのigraphパッケージでいうと、transivity(g, type ="global") で無向グラフの推移性を求めることができる。なお、transitivity()は有向グラフも無向グラフとして扱うようだ。エッジの向きを考慮したいんなら自分で求めろ、ってことでしょうか。
あるノードからみて、それと隣接するノードからなるサブグラフを考え、その密度(つまり、ありうるエッジの数に占める実際のエッジの数の割合)を求める。これをそのノードのクラスタ係数 clustering coefficient と呼ぶ。igraphパッケージではtransivity(g, type = "local")で求めることができる。
あるグラフについてノードのクラスタ係数を平均した値を、グラフのクラスタ係数という。igraphパッケージではtransivity(g, type = "average")で求めることができる。
このクラスタ係数というのはWatts & Strogatz (1998)が提案したのだそうだ。どっちもワッツさんたちである。なんだかなあ。
推移性とグラフのクラスタ係数はよく似ているんだけど、ちょっと異なる。
いったいどう異なるのか。なにがなんだかわかんなくなってイライラしてきたので、仕事を中断してメモを取った。
準備。
無向単純グラフ$G = (V,E)$について考える。つまり、エッジに向きはないし、自己ループもないし、2ノード間には辺があるかないかのどっちかで、エッジに重みなどというややこしいものはない。
ノード$v$に隣接するノード数を次数$d(v)$とする。
$G$の3つのノードからなる完全サブグラフを三角形と呼ぶ。ノード$v$を含む三角形の数を$\delta(v)$とする。グラフ全体について考える場合、ひとつ三角形が増えるだけで$\delta(v)$の合計は3増えるから、グラフ全体の指標としては
$\delta(G) = \frac{1}{3} \sum_{v \in V} \delta(v)$
がふさわしい。
ノード$v$を中間に持つ長さ2のパスを$v$のトリプルと呼ぶ。その数を$\tau(v)$とすると、$n$個から$k$個を取り出す組み合わせを$combn(n, k)$と書くならば$\tau(v) = combn(d(v), 2)$だ。合計すると
$\tau(G) = \sum_{v \in V} \tau(v)$
本題に戻ろう。
推移性とはなにか。それはトリプルの総数に占める三角形の総数だから、
$\displaystyle T(G) = \frac{3\delta(G)}{\tau(G)}$
である。
グラフのクラスタ係数とはなにか。
次数$d(v) \geq 2$のノードについて、ノードのクラスタ係数$c(v)$とは、トリプルの数に占める三角形の数、つまり$c(v) = \delta(v)/\tau(v)$である。グラフのクラスタ係数というのはこれを平均した値だから、次数2以上のノードの集合を$V'$として
$\displaystyle C(G) = \frac{1}{|V'|} \sum_{v \in V'} c(v)$
である。
なお、次数が1までのノードについてもなんらかクラスタ係数を決め(0だか1だか)、単純平均してしまうという方法もある。
ここで加重クラスタ係数というのを考えてみる。各ノードにウェイトとして正の実数$w(v)$が振られているとしよう。グラフの加重クラスタ係数を
$\displaystyle C_w(G) = \frac{1}{\sum_{v \in V'} w(v)} \sum_{v \in V'} w(v) c(v)$
とする。
仮に、トリプルの数をウェイトにしたら、つまり$w(v) = \tau(v)$としたらどうなるか。$c(v) = \delta(v)/\tau(v)$より、総和記号の右の$\tau(v)$は消えて、
$\displaystyle C_\tau(G) = \frac{\sum_{v \in V'} \delta(v)}{\sum_{v \in V'} \tau(v)} = T(G)$
となる。
つまり推移性とは、各ノードが持つトリプルの数を重みにした加重クラスタ係数のことだ。全ノードの次数が同じとき、ないし全ノードのクラスタ係数が一致しているとき、グラフのクラスタ係数と推移性は等しくなる。
以上、次の論文のイントロ部分よりメモ。
Shank, T., Wagner, D. (2005) Approximating clustering coefficent and transitivity. Journal of Graph Algorithms and Applications. 9(2), 265-275.
なるほどね...
グラフの特性を記述する際、推移性を使うべきなのだろうか、グラフのクラスタ係数を使うべきなのだろうか。たとえばある社会が「友達の友達もまた友達だ」的性質を持っているかどうかを調べるならば、ノードをベースに考えて後者を使い、たくさんの離散的状態を遷移していくなにかについて、そこでの遷移が「3期後には元に戻っちゃう」的性質を持っているかどうかを調べるならば、エッジをベースに考えて前者を使う、ということかなあ...
雑記:データ解析 - ちょっとした覚え書き:グラフの推移性とクラスタ係数はどうちがうか
2019年11月 8日 (金)
最近なんだかこんなことばっかりなんだけど...
Rで環境 (environment) と呼ばれるオブジェクトを操作したいとき、関数名がよく分からなくて困ることが多い。rlangパッケージというのを使うと、もっと使いやすい関数がわかりやすい名前で提供されていてありがたいんだけど、従来の関数との対応がわからなくて、それはそれで混乱する。
このたびついに業を煮やして、神Hadleyが与えたもうたAdvanced R 2nd edition, Chapter 7. Environments を参照しつつメモを取った。
すいません、私の私による私のためのメモです。
環境そのものの操作
- 環境をつくる: rlang::env(); new.env()
- 環境 e を表示する: rlang::env_print(e), print(e). ただしprint()では中身はわからない
- 環境 e の親環境: rlang::env_parent(e), parent.env(e)
- 環境 e のすべての先祖の環境: rlang::env_parents(e)
- 空の環境(すべての環境の始祖): rlang::enpty_env()
- グローバル環境(いわゆるワークスペース): rlang::globalenv(), .GlobalEnv
- サーチパス(グローバル環境の先祖の環境たち)の名前を返す: search()
- サーチパスの環境たちを返す: rlang::search_envs()
- baseパッケージのパッケージ環境 (そのパッケージが外部に提供する環境): rlang::base_env()
- 現在の実行環境(関数の実行中はその関数の実行環境、そうでない場合はグローバル環境): rlang::current_env(), environment()
- 現在の関数を呼び出している関数の実行環境: rlang::caller_env(), parent.frame()
- ある関数が実行されるときに生まれる実行環境の親は、その関数の「関数環境」である(呼び出し元の関数の実行環境ではない。ここ、ときどき勘違いしちゃいますね)。関数環境とは、その関数がつくられたときにそいつがbindしたというかキャプチャした環境のこと。対話的につくった関数の関数環境はグローバル環境、関数1のなかでつくった関数2の関数環境は関数1の実行環境となる。
- 関数 fの関数環境: rlang::fn_env(f), environment(f)
- パッケージのなかの関数の関数環境はそのパッケージの名前空間環境。その親はそのパッケージのimports環境。その親はbaseパッケージの名前空間環境。その親はグローバル環境。
環境の中身の操作
- 環境 e のなかの名前をみる: rlang::env_names(e), names(e), ls(e, all.names = T)
- 環境 e が要素 x を持っているかを調べる: rlang::env_has(e, "x"), exists("x", e)
- 環境 e の要素 x にアクセスする: e$x, e[["x"]]
- 環境 e の要素 x の値を得る(存在しないときにはエラーを発生させる): rlang::env_get(e, "x"), get("x", e, inherits = FALSE)
- 環境 e の要素 x に値 1 をbindする: rlang::env_poke(e, "x", 1), rlang::env_bind(e, x = 1); assign("x", 1, e).
- 環境 e の要素 x に表現myfun()をbindするが、そのときは評価せず、最初にアクセスしたときだけ評価する: rlang::env_bind_lazy(e, x = myfun()), delayedAssign("x", myfun(), assign.env = e)
- 環境 e の要素 x に関数myfunをbindする。アクセスするたびに評価する: rlang::env_bind_active(e, x = myfun), makeActiveBinding("x", myfun, e)
- 環境 e の要素 x を消す: rlang::env_unbind(e, "x"), rm("x", envir = e)。なお、e$x <- NULL では消せない。
- 永続付値 <<- は、先祖の環境たちのどこかにある変数を変更する。どこにもみつからなかったらグローバル環境に変数をつくる。現在の環境にある変数を変更したり、変数をつくったりすることはない
雑記:データ解析 - ちょっとした覚書:Rの環境を操作する関数
« 2019年10月 | メイン | 2019年12月 »
