« 読了:Clauset, Newman, Moore (2004) すごく大きなネットワークにおけるコミュニティ検出 | メイン | 読了:Teugels (1990) 多変量ベルヌーイ分布をどうやって表現するか »
2019年11月15日 (金)
用事があって、日帰りで長野の軽井沢というところに行った。有名な避暑地だが、これまでご縁がなく、記憶の限りでは初めての訪問である。
思ったより早く帰れることになったのだが、夕方の軽井沢駅は池袋駅並みにごった返しており、切符の都合で1時間半ほど時間を潰さなければならなくなった。駅の北側に少し歩いて、運よく喫茶店に空席をみつけた。
本でも読もうと思ったんだけど、ウェイターのお兄さんがコーヒーと一緒になにかをテーブルに置き、「時間つぶしにでもどうぞ...」という。それは木製の小さなパズルであった。ボードの上にイラストが描かれた小さなコマがいくつかあり、使い込まれてかすかに茶色い光沢を帯びている。コマを上下左右にずらし、目指す模様をつくるパズルだ。子供の頃にやったことがある。
「ははは」と愛想笑いしたけれど、そんなに暇そうに見えたかなあ、とちょっと気になった。もっともこれは私の気の回しすぎで、他のテーブルのお客さんにも渡していたようである。隣のテーブルの母娘連れも、親戚の悪口などを云いながらひとしきりこのパズルで遊んでいた。
鞄から本を取り出したが、こんな子供だましのパズルも懐かしいものだ、などと思い、頬杖をつき、戯れに指でコマを適当に滑らせてみた。完成したら本でも読もうか、と。
... それから1時間半。読書どころか、ぶっつづけでこのパズルに取り組む羽目になった。
解けない!解けないよ!
このパズル、めちゃくちゃ難しいじゃん!!
時間切れでお店を出るときにはイライラが極限に達しており、レジの横に並べられたこのパズルをひっつかんで買ってしまった。1300円、思わぬ出費である。店主らしき方が笑っていた。
帰りの新幹線でもこのパズルがぐるぐると頭をめぐって離れなかったのだが(「あの4つのリンゴを隣り合わせにして...」云々)、いやまてよ、と我に返った。レジ前の陳列には「日本一難しいパズル」と謳われていた。このパズル、たぶんほんとに難しい奴なのだ。いっぽう、私はあんまし頭の良いほうじゃない。パズルなんて大の苦手だ。なにも私が頑張って解くことはないんじゃないか。
むしろ、パズルを解くプログラムを書いたほうが早いんじゃないか?
問題
買ってきたパズルはこちら。
 コマをボードの外に出さずに移動させ、左上のこびとを右下の角に3つの柵でとじこめる、というのがゴールである。
コマをボードの外に出さずに移動させ、左上のこびとを右下の角に3つの柵でとじこめる、というのがゴールである。パズルももちろん著作物であり、勝手にブログに載せてはいけないと思ったのだが、検索してみたところ、喫茶店の方が画像を公開しておられることに気が付いた。これって、喫茶店の店主の方のオリジナル作品なのかしらん? すごいなあ。
お店の名前は「喫茶館丹念亭」。とてもよい雰囲気のお店で、コーヒーもシナモンケーキも美味しかった。いつかまた軽井沢に行く機会があったら立ち寄りたいと思います。
うちに帰ってビールを飲みながら再び試してみて、このパズルにはまった理由がなんとなくわかってきたような気がした。
このパズル、なんとなくコマをすべらせていると、なんとなく盤面が変化する。思いもよらぬ形で大きなコマが動いたときなど、ちょっとした快感がある。しかしよくみると、全く展望が開けていない。同じような局面をぐるぐると回っているだけで、そこから全く脱出できないのである。まるで迷路にはまり込んでしまったような気分だ。
よくわからんが、こういうパズルを考案するのってきっとすごい才能と努力の結晶なのであろうと思う。ほんとに尊敬します。
プログラムで解くにあたっての方針は次の通り。
- Rで書く。この課題にRが向いているからではなくて、単に私がRに慣れているからである。
- このパズルに限らず、このタイプのパズルすべてに適用できるプログラムにする。Wikipediaによれば、こういうパズルのことをスライディング・ブロック・パズル、ないしスライド・パズルと呼ぶらしい。知らなかった。
- 初期状態(つまり、最初のコマの配置)から出発し、そこからコマを動かして到達し得る状態を、力づくですべて探索する。なぜなら、どういう評価関数を書いたらいいのか、私にはよくわからんからである。
- 得られたすべての状態からなるネットワーク・グラフを生成する。パズルの解を求めるコードは書かない。だって、グラフが手に入っていれば、ネットワーク分析のソフトを使えば最短経路を探索できるじゃん?
- 朝までに書き終える。
我ながら頭の悪さがにじみ出る方針である。特に最後の奴がそうだ。結局、翌朝までには書けませんでした。
上で状態のネットワーク・グラフと書いたが、これはこういう意図である。
このパズルについていえば、最初にできるのは右上の柵を上に動かすことだけである。2手目にできることは2つある。右端列の下から2番目のリンゴを上に動かす、ないし、右から2つめのリンゴ2個のピースを上に動かしていくことである。3手目にできることは...
... と考えていくと、どんどん枝分かれしていくが、単純に増えていくだけではない。元の状態に戻ったり、別の手順でたどり着いた状態に一致したりすることもありうる。
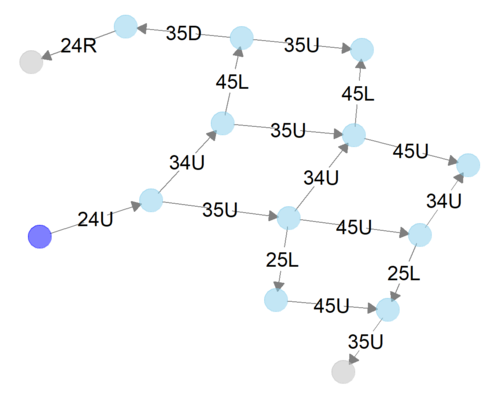
上図は5手までの状態を表現するネットワーク・グラフである。紫色のノード(円)は初期状態を表している。24Uとは「行2, 列4にあるコマを上に動かす」こと、つまり右上の柵を上に動かすことを意味している。
このように、5手までで14個の状態に到達できるわけだ。到達できる状態の数はどんどん増えていく。これをずーっと続けていけばさ!いつかはゴールに辿りつくよね!
後述するが、こういう過度に楽観的な態度、問題の難しさを最初に客観的に推し量ることを怠る姿勢が、人生の悲劇を招くのである。
これがパズルの解答だ
初期状態から到達し得る状態をすべて調べてみた。ただし、目標条件を満たす状態に辿り着いたら、そこからさらに探索するのはなし、ということにした。つまり、何も考えずにピースを動かしてはいるものの、ゴールに辿り着いたことに気がつかないほどアホではないプレイヤーが、いったいどのような盤面に辿り着きうるか、網羅的に調べたわけである。
軽井沢で買ったパズルの場合、手元のパソコンで約8時間で探索が終了した。8時間。映画を4本見られる時間、本を数冊読める時間、精力絶倫な王様なら子供をたくさん作れる時間だ。
すべての状態のネットワーク・グラフを描いてみた。それではご覧ください。軽井沢駅北口の喫茶店の店内でパズルのコマを動かしているみなさん! あなたはいま、この図の中のどこかにいますよ!
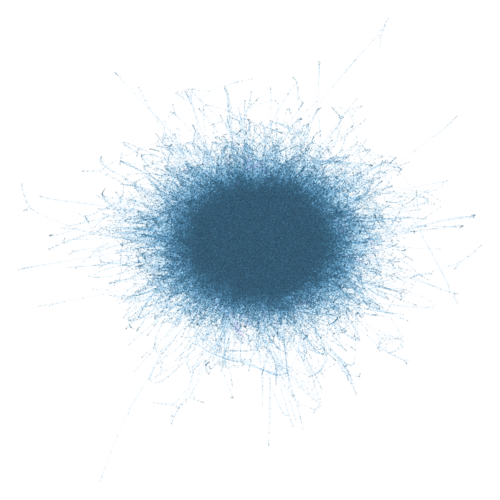
ネットワーク・グラフどころか、なにか模様のようなものしかみえないが、これはカメラをすごく引いているからで、目を凝らせば見えるであろう微小な点が個々の状態を表している。状態の数は977,412個。うち1個は初期状態、14個はゴールの条件を満たす状態である。
これではあまりに見にくいので、初期状態からゴールまでの経路(正確に言うと、14個のゴールそれぞれへの最短経路)の途中に位置する状態、計3,028個だけを抜き出して描いてみると...

青いノードが初期状態、ピンクのノードが経路上の状態、赤いノードがゴール状態である。
青いノードをお探しですか? 図右側のちょっと下寄りにあります。拡大してみましょう。
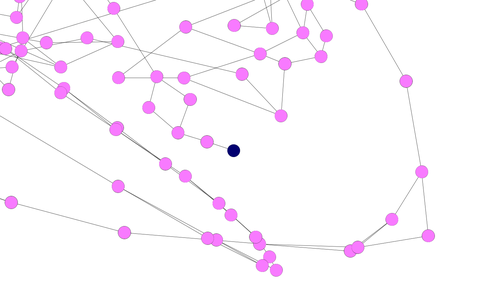
要は、この青いノードから辿って行けば、誰でもゴールにたどり着けるわけだ。
ああよかった、これで自分でパズルを解く必要がなくなった。夜もぐっすり眠れるというものだ。
ついでにいうと... 野暮なのでパズルの解答は書きませんけど、このパズルにおけるゴールへの最短経路は217手である。
買ってきたパズルには親切にも模範解答を図示した紙が添付されているのだが、その手数は254手(181手と記載されているが、ここではひとつのコマの1マスの移動を1手と数える)。おかげさまで、模範解答よりもすこし手数の少ない解答を見つけたことになる。ほんの少しだけ達成感があるが、いやいやそれよか、パズルを考案する人のほうがずっとすごいですよね。
だからどうした
だからどうしたんだこの暇人め、といわれると困ってしまうのだが、今回は自分なりにいろいろ学ぶところ大きかった。
帰りの新幹線のなかでぼんやり思ったのは、どうせ盤面の状態は限られているだろう、ということであった。盤面の大きさは4x5マス、コマの数は10個。喫茶店内でコマをあれこれ動かしているときも、なんだか同じ状態を行きつ戻りつしているような気がしてならなかった。だったら私にも全探索できちゃうんじゃない?と思ったのである。
振り返るとこれは無謀な賭けであった。組み合わせの数の大きさというものは人間の直感を遥かに超える。今回のパズルはたまたま初期状態から到達できる状態の全探索が可能であったし、あとで試算したところでは、そもそもこのパズルで可能な状態の数は1,281,550個しかない。しかし、問題が少し異なるだけで、状態の数は爆発的に増大し、まともな時間では到底全探索できないものとなっていただろう。
なんについてもいえることなんだろうけど、最初に問題の大きさを推し量ることって、すごく大事ですね。どうもそういう姿勢が私には欠けているようだ。反省。
なぜ難しいのか
それにしても不思議なのは、このパズルがなぜこんなに難しいのかという点である。実際に遊んだことがない方に、解のネタバレを避けつつ説明するのはすごく難しいんですが、とにかくほんとに難しいんですってば。イライラするんですってば。
難しい理由のひとつは、もちろん、ゴールまでの手順の多さであろう。しかしそれだけが要因ではないという気がしてならない。なんというか、いくらコマを動かしても、同じような局面をぐるぐると回っているように感じられるのである。
こうした難しさを、ネットワーク・グラフの形状によって定量的に示すことはできないだろうか。
同じような局面からなかなか脱出できないということは、ネットワーク・グラフのあちこちにノードの密な固まりがあって、その固まりから外に出て行くエッジが少ない、ということだろう。とすれば、ネットワーク・グラフ全体を通じてノードが局所的に固まっている程度を測ればよいのではないか。このパズルでは、その値がとても高くなっているのではないか?
思い悩んだ末、次のようなことを試してみた。
あるネットワーク・グラフについて、ノードをいくつかのグループにわけたとする。ネットワーク分析の慣例に従い、これをコミュニティと呼ぶことにする。
ノードの間のエッジは、同一コミュニティ内でつながるエッジと、コミュニティをまたがるエッジとにわかれる。前者のエッジの比率が大きいとき、コミュニティはネットワークのなかの密度の高い固まりをうまく捉えていることになる。
そこで、コミュニティ内のエッジの比率が、「そのグラフのエッジを一旦すべて消し、かわりに同じ数のエッジをランダムに張ったときに得られる、コミュニティ内のエッジの比率」と比べてどれだけ大きいかを調べる。これをモジュラリティという。うーん、下手な説明だが、要するに、モジュラリティが大きいことは、ノードがコミュニティの中で高密度に固まっていることを示しているわけである。
上のアイデアに従い、丹念亭パズルのネットワーク・グラフを徐々にたくさんのコミュニティに分割していき、そのたびにモジュラリティを測ってみよう。
どうやってコミュニティに分割するか。いろんな方法があるんだけど、ここでは手っ取り早く、Clausetたちの手法を使うことにする。これ、計算がすごく速いんです。
比較のために、すごくシンプルなスライドパズルについても同じことを試してみる。盤面は3x3, コマは8つ、サイズはすべて1x1であるパズルを考える。つまり、下図を3x3に縮めたようなパズルです。
このパズルについて、初期状態から辿り着くことができるすべての状態(181,440個)のネットワーク・グラフを作った。で、こちらについてもコミュニティ数を増やしながらモジュラリティを調べた。
結果は下図の通り。
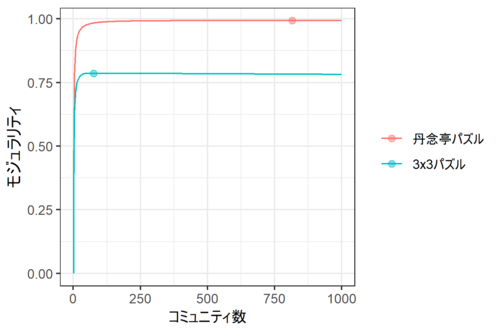
丹念亭のパズルではコミュニティ数816、3x3のパズルではコミュニティ数76のとき、モジュラリティが最大になった。
ここで注目したいのはモジュラリティの違いである。丹念亭パズルのモジュラリティは最大で0.993と、法外に高い。つまり、ネットワーク・グラフの描画からは読み取れないが、あたかも少量の水に溶かした小麦粉のダマのように、ノードが小さくて密度の高い固まりを形成しているのではないかと思う。そのため、やみくもにコマを動かしても、その固まりの外側になかなか出られない... ということではないかしらん?
疑問点
... などと書いてはみたものの、正直なところ、あまり自信がない。
- 3x3パズルは丹念亭のパズルよりも状態数が小さいし(9!=362880通り)、ネットワーク・グラフの作成にあたって目標状態を設定せずに全探索しているので、適切な比較になっているかどうかわからない。
- Clausetたちの手法は凝集的なコミュニティ検出手法なので、所与のコミュニティ数についてモジュラリティ最大のコミュニティを検出していないかもしれない。
- なにより、ここでモジュラリティに注目したのは良いやり方だったのだろうか。ネットワークがクラスタ化している程度を調べる際にはクラスタ係数と呼ばれる指標を使うことが多いと思うんだけど、スライド・パズルの状態のネットワーク・グラフはクリークを持たないので(3手で元に戻ることはできないから)、クラスタ係数は0となる。こういうネットワークについて、それがクラスタ化されている程度を調べるためにはどうしたらいいんだろう?
ううむ... このへんで時間切れということにしておくけど、いろいろ勉強が足りないことがわかった。
rSlidePzlパッケージ
軽井沢駅前の喫茶店でパズルを渡された副産物として、任意のスライド・パズルについて初期状態から到達しうる状態を全探索しネットワーク・グラフを生成するRパッケージ rSlidePzl を作りました。
ああ、私には聞こえる。任意のスライド・パズルについて初期状態から到達しうる状態を全探索しネットワーク・グラフを生成したいと思っている、世界三千万人の善人男女の歓喜の叫びが。(嘘です聞こえません)
パッケージはgithubからインストールできる。
このパッケージを使えば、お手元のスライド・パズル(9x9マス以内)について、初期状態から到達し得る状態をすべて探索し(幅優先探索)、みつかった状態からなるネットワーク・グラフをつくることができる。
せっかくなので、初期状態からゴールへの最短手順を出力する関数もつくっておいた。また、得られたネットワーク・グラフを(それが小さめであれば)簡単に描画できる関数もつくった。
探索すべきすべての状態を探索し尽くす場合、とんでもなく時間がかかることを覚悟する必要がある。これを避けるため、探索する手の深さ(何手目まで探索するか)や、探索する状態の総数について上限を指定し、探索を途中で打ち切ることもできる。
このパッケージを使って得られるネットワーク・グラフは igraph パッケージの igraph クラスのオブジェクトである。igraph パッケージが提供する多様な関数によって、その性質を心ゆくまで調べることができる。
コード例を示す。
### devtoolパッケージをインストール
### install.packages("devtools")### rSlikePzlパッケージをインストール
# devtools::install_github("shigono/rSlidePzl")### rSlikePzlパッケージをロード
library(rSlidePzl)library(tidyverse)
library(igraph)### セッティング
oSetting <- makeSetting(
## 盤面のサイズ (行サイズ, 列サイズ)
boardsize = c(4,5),
## コマのサイズ (行サイズ, 列サイズ)
piecesize = list(
A = c(2, 2), # コマタイプA.こども パズルに添付されている解答ではNo.1
B = c(2, 1), # コマタイプB.りんごとサク No.5
C = c(1, 2), # コマタイプC.横長のサク No.7
D = c(1, 1), # コマタイプD.りんご, No.2,3,9,10
E = c(2, 1), # コマタイプE.縦長のサク, No.6
F = c(2, 1), # コマタイプF.縦長のりんご No.8
G = c(1, 2) # コマタイプG.横長の林檎 No.4
)
)### こどものピースの位置(1,1), (1,2), (2,1), (2,2)について考える
anNumStates <- sapply(
list(c(1,1), c(1,2), c(2,1), c(2,2)),
function(anLoc){
### 可能な状態の数を算出する
getNumStates(
makeState(
list(
makePiece(type = "A", loc = anLoc),
makePiece(type = "B", loc = c(NA,NA)),
makePiece(type = "C", loc = c(NA,NA)),
makePiece(type = "E", loc = c(NA,NA)),
makePiece(type = "F", loc = c(NA,NA)),
makePiece(type = "G", loc = c(NA,NA))
)
),
oSetting
)
}
)
# - こどものピースが位置(1,1)(左上端)であるときの状態数は、
# 左下端(3,1), 右上端(1,4), 右下端(3,4)にあるときの状態数と同じはずなので、4倍する
# - こどものピースが位置(1,2) にあるときの状態数は、
# (1,3), (3,2), (3,3) にあるときの状態数と同じはずなので、4倍する
# - こどものピースが位置(2,1) にあるときの状態数は、
# (2,4) にあるときの状態数と同じはずなので、2倍する
# - こどものピースが位置(2,2) にあるときの状態数は、
# (2,3) にあるときの状態数と同じはずなので、2倍する
# 各状態においてりんごのピースを置く位置は6 x 5 / 2 通りあるから...
print(sum(anNumStates * c(4,4,2,2)) * 6 * 5 / 2) # 状態数は1281550### 開始時点の盤面の作成
oStart <- makeState(
list(
makePiece(type = "A", loc = c(1,1)), # パズルに添付されている解答ではNo.1
makePiece(type = "B", loc = c(1,3)), # No.5
makePiece(type = "C", loc = c(2,4)), # No.4
makePiece(type = "D", loc = c(3,1)), # No.2
makePiece(type = "D", loc = c(3,2)), # No.3
makePiece(type = "E", loc = c(3,3)), # No.6
makePiece(type = "F", loc = c(3,4)), # No.8
makePiece(type = "D", loc = c(3,5)), # No.9
makePiece(type = "G", loc = c(4,1)), # No.4
makePiece(type = "D", loc = c(4,5)) # No.10
)
)
stopifnot(isValidState(oStart, oSetting))### 目標条件の作成
oGoalCondition <- makeState(
list(
makePiece(type = "A", loc = c(3,4)), # No.1
makePiece(type = "B", loc = c(1,3)), # No.5
makePiece(type = "E", loc = c(3,3)), # No.6
makePiece(type = "C", loc = c(2,4)) # No.7
)
)
stopifnot(isValidState(oGoalCondition, oSetting))### 5手だけ検索
oGraph <- makeGraph(oSetting, oStart, oGoalCondition, verbose = 1, max_depth = 5)### 描画
set.seed(123)
plotGraph(oGraph, method = "GGally")### すべての手順を探索。手元のパソコンで8時間くらい
oGraph <- makeGraph(oSetting, oStart, oGoalCondition, verbose = 1)### 目標条件を満たした状態を表示
print(V(oGraph)[V(oGraph)$status == 4])### 目標条件を満たした状態への最短経路を表示
print(getShortestPath(oGraph)$transition)### コミュニティ検出。fast_greedy法でmodularityを最適化する
oGraph_undirected <- as.undirected(oGraph)
oCommunity <- cluster_fast_greedy(oGraph_undirected, modularity = TRUE)### 描画。Rでは大変なのでGephi (https://gephi.org/) で描く。
### グラフに描画のための属性を追加する
### state_color属性: {1(初期状態),2(目標状態),3(目標への途中),4(ほか)}
### Gephiでこの属性をcolorに指定すると、ノードを色分けできる
anColor <- rep(4, length(V(oGraph))) # 4: 下記以外の状態
anColor[getReachability(oGraph) == 1] <- 3 # 3: 目標状態に至るパス上にある状態
anColor[V(oGraph)[V(oGraph)$status == 4]] <- 2 # 2: 目標状態
anColor[1] <- 1 # 1: 初期状態
V(oGraph)$state_color <- anColor### state_size属性: {1(目標への経路上にない),2(ある)}
### Gephiでこの属性をsizeに指定すると、目標への経路上のノードを大きくできる
V(oGraph)$state_size <- c(2,2,2,1)[anColor]
V(oGraph)$state_comm <- membership(oCommunity)### state_x属性, state_y属性: x座標とy座標
### GephiのGeo layoutでこれらの属性を緯度経度に指定すると、レイアウトを再現できる。
### コミュニティ内のエッジに大きな重みを与え、Fruchterman-Reingoldアルゴリズムで
### 最適化している。Gephiでレイアウトを作成してもいいけど、こっちのほうが速い
oLayout <- layout_with_fr(
oGraph,
weights = ifelse(crossing(oCommunity, oGraph), 1, 10),
niter = 1000
)
### 座標が大きな値だとメルカトル図法では歪んでしまうので、-1から+1に基準化する
oLayout <- norm_coords(oLayout)
V(oGraph)$state_x <- oLayout[,1]
V(oGraph)$state_y <- oLayout[,2]### graphml形式で出力。このファイルをGephiで読み込む
write.graph(oGraph, file = paste0("./full_states.graphml"), format = "graphml")### 3x3パズルのセッティング
oSetting <- makeSetting(
boardsize = c(3,3),
piecesize = list(
A = c(1, 1), B = c(1, 1), C = c(1, 1), D = c(1, 1),
E = c(1, 1), F = c(1, 1), G = c(1, 1), H = c(1, 1)
)
)
oStart <- makeState(
list(
makePiece(type = "A", loc = c(1,1)),
makePiece(type = "B", loc = c(1,2)),
makePiece(type = "C", loc = c(1,3)),
makePiece(type = "D", loc = c(2,1)),
makePiece(type = "E", loc = c(2,2)),
makePiece(type = "F", loc = c(2,3)),
makePiece(type = "G", loc = c(3,1)),
makePiece(type = "H", loc = c(3,2))
)
)
stopifnot(isValidState(oStart, oSetting))### 3x3パズルのネットワーク・グラフ作成
oGraph_Nine <- makeGraph(oSetting, oStart)### 上と同じやり方でコミュニティ検出
oCommunity_Nine <- cluster_fast_greedy(as.undirected(oGraph_Nine), modularity = TRUE)### モジュラリティ比較
oGraph_undirected <- as.undirected(oGraph)
anModularity <- sapply(
1:1000,
function(nNum){
modularity(oGraph_undirected, cut_at(oCommunity, no = nNum))
}
)
oGraph_undirected <- as.undirected(oGraph_Nine)
anModularity_Nine <- sapply(
1:1000,
function(nNum){
modularity(oGraph_undirected, cut_at(oCommunity_Nine, no = nNum))
}
)
dfPlot <- data.frame(
nNumComm = 1:1000,
nMod_1 = anModularity,
nMod_2 = anModularity_Nine
) %>%
gather(sVar, gValue, c(nMod_1, nMod_2)) %>%
separate(sVar, c("sVar1", "nVar2")) %>%
group_by(nVar2) %>%
mutate(bMax = if_else(gValue == max(gValue), 1, 0)) %>%
ungroup() %>%
mutate(fGraph = factor(nVar2, levels = c("1", "2"), labels = c("丹念亭パズル", "3x3パズル")))
g <- ggplot(data = dfPlot, aes(x = nNumComm, y = gValue, color = fGraph))
g <- g + geom_line()
g <- g + geom_point(data = dfPlot %>% filter(bMax == 1), size = 2, alpha = 0.5)
g <- g + labs(x = "コミュニティ数", y = "モジュラリティ")
g <- g + scale_color_discrete(name = NULL)
g <- g + theme_bw()
print(g)### 以上
githubを使うのも、Rパッケージを公開するのもはじめてなので、いろいろ不備があるかもしれませんが、そのへんはひとつ、ご愛敬ということで...
雑記:データ解析 - 軽井沢駅前の喫茶店の店員さんに渡されたパズルを解く (ためのRパッケージを作った)
