« 読了:08/31まで (NF) | メイン | 読了:09/06まで (C) »
2009年9月 6日 (日)
勤め先で検定力関数のグラフを描く用事があった。サンプルサイズを横軸に,仮説検定で得られる検定力を縦軸にプロットした折れ線グラフ。たまにはそういう変わった仕事もある。
必要なグラフは描けたので,戯れにパラメータをいろいろ変えてみては,グラフの様子が変化するのを,頬杖をついてぼんやり眺めていた。ふつうの検定力関数は滑らかな単調増加曲線だが,パラメータによってはガタガタの階段状になったり,ノコギリの歯みたいな形になったりする。ふうん,面白いなあ。さて,昼飯でも食いに行くか,と席を立った。で,ぼーっと外に出て,ぼけーっと交差点をわたり,ぼんやりコーヒーを啜っているあたりで,はた,と気が付いた。
ノコギリの歯?! それはつまりその,サンプルサイズを増やすと検定力が下がることがある,ということですか? ま・さ・か,そんなはずがない。。。
このブログを誰が読んでいるのかわからないが,なかには俺の同類,すなわち自分に統計学の知識が欠けていることを認めたがらない哀れな解析ユーザもいるだろう。そういう人はきっと,やれやれ,こいつ幻覚でも見るようになったか,と思うに違いない。
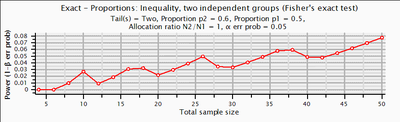
証拠を載せておこう。下に貼ったのは独立二群間の比率差の検定における検定力曲線(母比率60%と50%,α=.05,標本サイズは群間で等しい)。いまG*Power3で描いた。
このグラフはFisherの正確検定の場合。たとえばN=18(群あたりN=9)の場合の検定力は3%,N=20の場合の検定力は2%であり,二例ふやしたせいで検定力が落ちてしまう,ということがわかる。こういうことがあるんですね。専門家には鼻で笑われちゃうかもしれないけど,俺は驚いた。これで統計学の講義などやってたんだから,ホントに申し訳ない。言い訳になりますが,心理学出身者は正確検定なんてあんまり使わないんです。
しばらく考えて自分なりにようやく納得したのだが,このからくりは,棄却のための臨界値を決めるとき,与えられたNの下でα=.05以下となる上限を求める,という点に由来するんじゃないかと思う。その結果として達成されるactualなαは往々にして.05を下回ってしまう。上記の例の場合,α=.05, N=20の下で,実際のαは実に.012である。名目的なα=.05からのギャップが大きい分だけ,無駄に保守的になっている,つまり,検定力を失っていることになる。
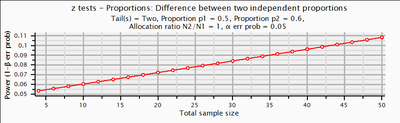
というわけで,このような例はFisherの正確検定に限らず,検定統計量の分布が離散的なときには常に生じうる。いっぽう下のグラフのように,Pearsonのカイ二乗検定のような漸近法では生じない。
ついでに関連論文を一本読んでみた。ここまでくると,仕事に役立つわけではないので,純粋に趣味というべきである。
Chernick,M.R., Liu,C.Y. (2002) The Saw-Toothed Behavior of Power versus Sample Size and Software Solutions: Single Binomial Proportion Using Exact Methods. The American Statistician. 56(2), 149-155.
SAS のマニュアルで引用されていた論文。検定力関数がノコギリ状になることがある点を指摘したうえで,市販ソフトがそれにどう対応しているかを紹介している。問題はノコギリ状になることそのものではなく,検定力からサンプルサイズを決定する際に,ソフトがちゃんと事態を説明してくれるか,という点にあるようだ。つまり,たとえば「ご指定の検定力を達成するためにはN=18必要です」と出力されたとして,読み手はうっかり「なるほど,N=18以上あればいいんだな」と思ってしまうが,実はそうではないかもしれない。ソフトはそのことをちゃんと教えてくれるか,ということである。なるほどね,そういう業界の人にとってはシビアな話であろう。
なお,取り上げられていたソフトはnQuery Advisor, Power and Precision, StatXact, PASS, UnifyPow。最後のやつはSASのマクロで,SAS 9.1から実装されたPOWERプロシジャの元になったらしい。
論文:データ解析(-2014) - 読了:09/06まで (A)