« 読了: Tadajewski(2006) モチベーション・リサーチ、その勃興と衰退 | メイン | 読了:「カブのイサキ」「オールラウンダー廻」「花咲さんの就活日記」「ラブやん」「犬神姫にくちづけ」「千年万年りんごの子」「87 CLOCKERS」 »
2013年5月19日 (日)
このブログを書き始めてからずいぶん経つが、所詮は自分のための備忘録に過ぎない。いちばん熱心な読者はたぶん私だ。書店の棚に平積みになっている連載マンガのこの巻を、俺はもう読んだだろうか? と疑問に思った際、このブログはとても重宝する。店頭でスマフォと格闘している姿は、あまり格好のよいものではないけれど。
そもそも私には世の中に訴えたいことが特にない。とりたてて語るべき知恵もない。アクセスログを調べると、過去のいくつかの記事が予想外に多くの方に読まれていることに驚くが(片側検定について書いた記事とか)、もっときちんとした専門家がお書きになったものをご覧いただいたほうが良いわけで、少し申し訳なく思っている。
これから書くのは、このブログを書き始めて以来ほとんどはじめて、純粋に自分以外の誰かのために載せる記事だ。特に、検索エンジン経由でたどり着く方に向けて載せる記事だ。
振り返ってみると、私は何年か前から、だいたい年に数回のペースで、以下の内容をどなたかに説明している。聞き手にとっては面倒で退屈な内容だ。説明に成功することもあれば失敗することもある。偉大なるインターネットの力によって、説明の回数を減らし成功率を上げたい。
というわけで、ずっと前にお問い合わせに応じて書きためていた文章を載せておくことにする。どうかこの記事が、正しい内容を正しいやりかたで説明していますように。そしてgoogleの検索結果の上の方に出てきますように。
以下の内容はとても単純である。たった一言で要約できる。
統計ソフトがいう「ウェイト」は、調査でいう「ウェイト」ではない。
もう一度書きます。SPSSとかSASとか!そういう統計ソフトの! ウェイトとか重み付けとかっていうのは! 調査でいうところの! いわゆるウェイトのことではないです!
。。。このくらい大声で書いておけば、検索されやすくなるだろうか。
調査における「ウェイティング」
市場調査の会社にお世話になって驚いたことのひとつは、結果の集計に際してウェイティング(確率ウェイティング)を実に良く使う、ということである。親の仇かというくらいによく使う。
確率ウェイティングとはこういう話だ。
ある集団の性質について調べるため、その集団に属する人を対象に調査を行った。調査対象者がこの集団を互いに独立に偏りなく反映していると仮定し、得られたデータから統計的推測を行いたい。
さて、私たちはこの集団(対象母集団)における男女比が5:5であると知っている。しかしなにかの事情によって、調査対象者の男女比は7:3にならざるを得なかった。この事情にはいろんな種類がありうるが、たとえば調査設計時の事情が考えられる(比例割当でない層別抽出)。
この調査対象者の回答をそのまま集計し、平均や割合を求めてしまうと、その値は男の回答をより強く反映してしまい、母集団の推測としては歪んだ値になってしまう。
これを避けるために、男の回答には小さな重み(ウェイト)、女の回答には大きな重みを与えて集計する。これが調査でいうところのウェイティング、すなわち確率ウェイティングである。
なお英語では、probability weighting, survey weighting, sampling weightingなど、いろいろな呼び方が用いられている。検索するときに困る。
市場調査の業界団体である日本マーケティング・リサーチ協会がまとめた「マーケティング・リサーチ用語辞典」を見ると、「ウェイトつき集計」という項で確率ウェイティングが説明されている。市場調査に限らず、広義の社会調査全般において、ウェイト、ウェイティング、ウェイト・バックという言葉は確率ウェイティングを指して使われることが多いと思う。
確率ウェイティングと拡大推計
確率ウェイティングは拡大推計とごっちゃにして語られることもある。
たとえば、前掲の業界団体による市場調査会社向けガイドラインには、ウェイティングについての注意点を挙げている箇所がある。
一般的にウエイトバックが必要となる理由は
1. 層化サンプリングの段階でウエイト付けする場合
2. 回収率の違いにより標本構成に偏りが出てそれをウエイト付けにより補正する場合
上記2点が多いと考えられるが、[中略] ウエイト付けをした場合、主な表すべてにおいて、ウエイト付けした基数(ベース)としない基数(両者を明確に区別)を明示すること。
前半はどうみても確率ウェイティングに関する説明である。ところが後半では、「ウェイト付けした基数」という文言が登場する。ウェイティングしようがしまいが標本サイズは標本サイズなのであって、これは意味不明である。
実は、「1000人の対象者のうち3000人がこの製品を買いたいと答えた、市場には潜在顧客が1000万人いるから、発売すればきっと300万人が買ってくれるだろう」というような単純な拡大推計を指して「ウェイティング」ということもある。
ガイドラインの文言は、確率ウェイティングと拡大推計の両方について同時に述べているようである。
確率ウェイティングは標本の性質に応じて必要となるもので、あらゆる統計的分析に影響する。いっぽう、拡大推計は標本の性質とは無関係に要請され、要約統計量のなかでも合計にしか影響しない。クロス集計の手順のみについて考えれば似たようなものかもしれないが、このふたつは分けて考えたほうが良いと思う。
ウェイティングした分析はできますか?
調査データの分析において確率ウェイティングはどんなときに必要か。仮に必要だとして、ウェイトはどうやって求めるか。
これはなかなか難しい問題で、容易な答えはない。悩みの種である。あまりに悩んだ末、高名な専門家による解説を全訳してしまったことさえある。若気の至り、窓の雪。しかしその話は脇に置いておく。
本題は、確率ウェイティングのためのウェイトが各ケース(ローデータの行)に対してすでに付与されているとき、そのウェイトを用いながらさまざまな統計的推測を行うことができるか、という点である。つまり、統計ソフトを使い、データに確率ウェイティングを行いつつ、差の検定を行ったり、相関を求めたり、回帰分析や因子分析を行ったりすることができるか(行うべきかどうかは別にして)、という点である。
私は繰り返し説明してきた。できません。十中八九できません。なぜなら、お使いの統計ソフトがいうところの「ウェイト」は、私たちが思っているような意味でのウェイトではないからです。
手計算による確率ウェイティング
ごく簡単な例について考えよう。
母集団における男女比は5:5。事情があって、標本における男女比が7:3となるように設計した。母集団は十分に大きいものとする。非現実的ではあるが、標本サイズは男7, 女3, 計10であるとしよう。
この10人が、ある変数について次のような値を持っている。
| 男性 | 1, 2, 2, 3, 3, 4, 4 |
|---|---|
| 女性 | 1, 2, 3 |
このデータに基づき、母集団におけるこの変数の平均(母平均)について推測したい。
まずは、統計ソフトを使わずに考えてみよう。ひとまず男性に注目する。標本平均は、(1+2+2+3+3+4+4)/7=2.714。つまり、母集団における男性の平均は2.714と推定される。
この推定はどのくらいあてになるだろうか。標本平均の分散を求めよう。統計学の初級の教科書に書いてあるように、標本平均の分散は (不偏分散)/(標本サイズ) である。ええと、不偏分散は1.238, 標本サイズは7 だから、標本平均の分散は1.238/7=0.177だ。
同様に女性についても電卓を叩いてみると、標本平均は2.000, 標本平均の分散は0.333である。
では、全体の平均について考えよう。いま、男性の平均が2.714、女性の平均が2.000と推定されていて、かつ母集団のうち男性は5割、女性は5割であることがわかっているのだから、男女をあわせた平均は 2.714*0.5 + 2.000*0.5 = 2.357 と推定できる。
この推定はどのくらいあてになるか。推定量の分散は、{(男の標本平均の分散) * (男の割合)^2 + (女の標本平均の分散) * (女の割合)^2} となる (ご不審の向きは、L. Kish "Survey Sampling"(Wiley) の80-82頁、豊田秀樹「調査法講義」(朝倉書店) の131-132頁をご覧ください)。ええと、0.177*0.25 + 0.333*0.25 = 0.128である。
以上が「正解」である。表にまとめておく。なお、標本平均の分散の平方根は標準誤差と呼ばれ、広く用いられているので、それも添えておく。
| 母平均の推定値(標本平均) | その分散 | 標準誤差 | |
|---|---|---|---|
| 男性 | 2.714 | 0.177 | 0.421 |
| 女性 | 2.000 | 0.333 | 0.577 |
| 全体 | 2.357 | 0.128 | 0.357 |
手計算による確率ウェイティング(ケース・ウェイトを用いて)
この計算を、個々のケースにウェイトを与える形で表現しなおしてみよう。
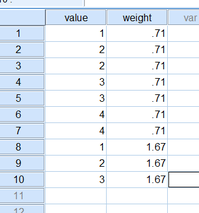
まず、各ケースにウェイトを与える。このウェイトは、ケースが母集団から抽出される確率の逆数に比例した値であればなんでもよいのだが、一番わかりやすいのはこういう求め方だ。母集団における男の割合は5割、標本では7割だから、男のウェイトは5/7=0.714。同様に、女のウェイトは5/3=1.667。ウェイトの合計は10となる。
母平均の推定値、すなわち「ウェイティングされた標本平均」を求める際には、個々の値にウェイトを掛けながら合計し、ウェイトの合計で割る。{1*0.714 + 2*0.714 + ... + 2*1.667 + 3*1.667) / 10 = 2.357。
上記の結果とぴったり一致する。計算式を変形しただけだから、当たり前である。
SPSSで試してみると
では、統計ソフトを使って試してみよう。みんな大好きな IBM SPSS Statistic での例を紹介する (ver.19で試しました)。下図のデータを用意する。クリックすると大きくなるはずです。
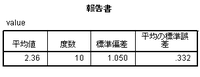
SPSSのメニューには[データ]-[ケースの重み付け]という機能がある。こいつはきっと確率ウェイティングの機能にちがいない、というわけで、「ケースの重み付け」を選び、変数weight を指定してみよう。次に、[分析]-[グループの平均]で変数valueの平均を求める。[オブション]で「平均値の標準誤差」を選んでおく。アウトプットは...
平均値は2.357。「正解」と一致する。ところが、平均の標準誤差は0.332。「正解」よりも少し小さい。
平均の標準誤差なんてどうでもいいです、などというなかれ。たいていの推測統計手法は標準誤差と関係している。みんなが死ぬほど大好きな検定だって、もちろんそのひとつだ。標準誤差が誤りなら、検定の結果だって誤りだ。これはとても大事な話なのである。
頻度ウェイティング
なぜこのような結果になるのか。理由は拍子抜けするほどに簡単だ。
SPSSでいう「ケースの重み付け」は確率ウェイティングのことではない。それは単に「ウェイトの数だけこのケースをコピーしてくれ」ということである。
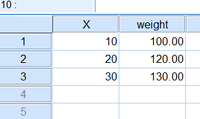
たとえば上の3行のデータを与え、変数weightで「ケースの重み付け」を行うと、SPSSはこう考える。変数Xが10である行が100行、20である行が120行、30である行が130行、全部で350行のデータなんですね、わかりました、と。
こうした機能は「頻度ウェイティング」と呼ばれることがある。頻度ウェイティングはデータ行列のサイズを小さくするための工夫に過ぎない。
頻度ウェイトによってコンパクトに表現されたデータ行列を一発で扱う方法について考えてみよう。ある変数の標本平均を求める際には、個々の値に頻度ウェイトを掛けながら合計し、頻度ウェイトの合計で割ればよい(なぜなら、頻度ウェイトは本来のローデータにおけるケース数だから)。
この式は、幸か不幸か、確率ウェイティングのもとで母平均の推定値を求めるための式と、た・ま・た・ま、同じ形になっている。そのせいで、SPSSがウェイトを頻度ウェイトとみなして求めた標本平均は、同じウェイトが確率ウェイトだった場合の母平均の推定値 2.357 と、た・ま・た・ま、一致する。だからといって、SPSSが確率ウェイトを正しく扱えるわけではない。
なお、SPSSにとってはウェイトは頻度なのだから、それは整数でないとおかしい。さきほどはウェイトとして整数でない値を与えたが、よくもエラーにならないものである。実際、上記で試した[分析]-[グループの平均]は、整数でないウェイトをむりやり頻度として捉えるが、他の機能は、ウェイトを整数に丸めてしまったり、そもそも無視してしまったりすることがあるらしい。
分析ウェイティング
もうひとつの有名な統計ソフトであるSASでは、また少し話が違う。
SASでは各プロシジャのweight 文でケース・ウェイトを指定できる。その扱いはプロシジャによっても設定によってもちがうのだけれど、通常は、「このデータの行はサブグループの平均を表していて、それぞれのグループのサイズがウェイトで表されているのね」という意味に解される。
たとえば、さきほどの3行のデータをSASに与え、weight列をケース・ウェイトに指定すると、通常は次の意味になる。「サブグループ1はサイズ100, Xの平均は10だった。サブグループ2はサイズ120, Xの平均は20だった。サブグループ3はサイズ130、Xの平均は30だった。」
こうしたウェイティングは「分析ウェイティング」と呼ばれることがある。これもまた、確率ウェイティングではない。
統計ソフトにおける「ウェイティング」とは
統計ソフトの中には確率ウェイティングを扱うことができるものもある。
- SASのsurveymeanプロシジャは、複雑な標本抽出によるデータのために特に用意されているプロシジャで、確率ウェイトを正しく処理することができる。先ほどのサイズ10のデータをsurveymeanプロシジャに与えると、全体の平均は2.357, 標準誤差は0.357、手計算による「正解」とぴったり一致する。
- SPSS StatisticsにはComplex Samplesというパッケージが用意されているらしい。別料金で。
- 経済統計の分野で有名なStataは、与えたウェイトが確率ウェイトなのか頻度ウェイトなのか分析ウェイトなのかを指定できるそうである。
- Rにはsurveyというパッケージがある。
- 公的調査の分野ではSUDAANというソフトが有名である。検索すると茨城県大洗町の割烹「寿多庵」が引っかかるので困ってしまう。あんこう鍋がおいしいらしい。
- 構造方程式モデリングのソフト Mplus は確率ウェイティングに対応している。
- 最後に、世の中には調査データのクロス集計だけに特化した業務用ソフトというものがあって、それらのソフトは、(これも長い話になるのだが)基本的には、確率ウェイティングを伴う検定を正しく行うことができる模様である。
そういうソフトでないかぎり、お使いの統計ソフトでは ... もっと具体的にいえば、SPSS Statistic BaseならびにAdvanced Statistics、SAS/BASEならびにSAS/STATのsurvey系プロシジャを除く全プロシジャ、その他もろもろの統計ソフトでは ... 確率ウェイティングを伴う分析を行うことはできない。メニューに「重み付け」という機能があっても、プロシジャにweight文というのがあっても、それは確率ウェイティングではない。
考えてみれば、統計ソフトのユーザは多方面にわたるが、確率ウェイティングをしたいと思う人はせいぜい市場調査・社会調査の関係者くらいであろう。一般的な統計ソフトのメニューにある「重み付け」が、調査実務家の考える意味でのウェイティングでないとしても、文句をいえる筋合いではない。
ややこしいのは、確率ウェイティングに対応していないソフトに誤って確率ウェイトを与えて要約統計量を求めたとき、平均と割合だけは期待通りの値が出力されることがある、という点である。繰り返しになるが、それはた・ま・た・まである。他の結果は誤っている。
統計ソフトがいう「ウェイト」は、調査でいう「ウェイト」ではない。
あえて教訓を求めるならば
最初に書いたように、私には世の中に訴えたいことは特にない。とりたてて語るべき知恵もない。ただ単に、日頃繰り返している説明を文章にしておき、仕事を楽にしたいだけである。
しかし、あえて教訓らしきものを引き出すとすれば、こういうことはいえる。
私の説明にオリジナリティはない。webを探せば、もっとわかりやすい説明がみつかる。たとえばこちらやこちら。統計ソフトのアウトプットをこまかーく調べた面白い研究もある(PDF)。
さらに、SPSS Statisticsを起動し[ケースの重み付け]ダイアログの[ヘルプ] ボタンを押すと、次の説明が現れる。
[ケースの重み付け] では、統計分析を行うため (複製をシミュレートすることにより) ケースに異なる重みを付けることができます。重み付け変数の値は、データ ファイル内の 1 つのケースが表す観測数を示していなければなりません。いささか不親切ではあるけれど、簡にして要を得た説明である。この記事で長々と書いてきたことはすべて、ソフトのマニュアルに、はっきりと書いてあることなのだ。
にもかかわらず、推定や検定やもっと複雑な統計的分析の際に、SPSS Statisticsの[ケースの重み付け]で確率ウェイティングを行おうとしている方に、私はこれまでたくさん出会ってきた。それはもう、びっくりするくらいにたくさん。そのなかには、すごく優秀な分析者もいらっしゃったし、調査実務に携わって何十年というベテランの方もいらっしゃった。
というわけで、教訓はこうだ。実務家の豊富な経験なるものは、必ずしもあてにならない。統計ソフトの使い方を先輩に教わったり、誰かの書いたブログを読んでいる暇があったら、そのソフトのマニュアルを読んだほうがよいのではないかと思います。
雑記:データ解析 - 統計ソフトの「ウェイト」は調査の「ウェイト」ではない