« 読了：Hui, Huang, Suher, & Inman (2013) 買物客の行動データで非計画購買を解剖する | メイン | 読了：Millsap(2007) 測定不変性と予測不変性は両立しないことをなぜみんなわかってくれないのかしら »
2014年3月30日 (日)
このブログの趣旨に反して、これから書くのは私の覚え書きではなく、他の方に読んでもらうための文章である。どうか私が事柄を正しく説明していますように。そしてこのエントリが、検索結果の上の方に出てきますように。
市場調査に関連する仕事で糊口を凌いでいるのだけれど、折々に受ける業務上のご質問のなかでかなりの領域を占めているのが、いわゆる「ウェイトバック集計」、すなわち確率ウェイティングに関するあれこれである。
もっとも基本的な質問はこういうのだ。「ウェイトバックしたほうがいい？しないほうがいい？」 これはですね、ほんとに答えに困ります。
いま手元に標本抽出確率が不均一な標本があり、集計・分析の際にウェイティングすべきかどうかが問われたとき、考慮すべきポイントは、主に4つあると思う。
- (1)適切なウェイトが構成できるのか。
- (2)それだけの能力とやる気があるか。
- (3)ウェイティングによって推定量の誤差は小さくなると期待できるか。
- (4)ウェイティングによるバイアスの除去という発想は、分析に際しての諸前提と整合するか。
(1) については誤解がないと思う。(2)についてはいろいろ誤解があり、以前義憤に駆られて思うところを書いた。(4)は話がすごく長くなる。
問題は(3)である。実のところこの論点こそが、調査実務に関わる人にとっての道しるべ、ウェイティングの是非という難しい問題に光を差してくれる灯火となると思うのだけれど、不思議なことに、この点についてきちんと説明した日本語の資料をほとんどみたことがない。同業種の方々と話していても、誠に失礼ながら、この点についてきちんと理解しておられる方は非常に少ないように思う。あまりに少ないので、ひょっとして私が全てを勘違いしているのではないかと不安になるほどだ。
(3)について誰かに説明しなければならない羽目に陥ることもある。これが結構大変なのである。できれば避けて通りたい。いまはなんでも検索する時代だから、いちど文章にしてブログかなにかに書いておけば、そのぶん説明の回数も減らせるかもしれない。もし私が全てを勘違いしているのならば、それを指摘してくださる奇特な方が現れないとも限らない。
以上が、この文章を書く主たる理由である。実はもうひとつ、ついうっかりwebアプリをつくってしまったというささやかな理由もあるのだけれど、それはあとで。
問題
以下では、いわゆる「ウェイト・バック集計」、すなわちデータの集計・解析における確率ウェイティングについて考える。上記の4つのポイントのうち(1)(2)(4)はすでにクリアされていることにする。
調査データの解析で確率ウェイティングが登場する局面は意外なほど多岐にわたるのだけれど(Kish(1990)は7種類挙げている)、説明に際しては、もっともわかりやすくて一般的な、非比例の層別抽出を想定する。集計対象は二値変数で、母集団全体における割合に関心があることにする。母集団は十分に大きいことにする。
あまりにシンプルすぎて非現実的ではあるが、次の場面について考えよう。ある新製品コンセプトに対する消費者の購入意向を調べたい。そこで潜在的顧客から抽出した調査対象者に、その製品を買ってみたいどうかを「はい/いいえ」で聴取した。以下、「はい」と答える人の割合のことを購入意向率と呼ぶことにする。
性別で層別した標本抽出を行った。つまり、男と女のそれぞれについて、決まった数の調査対象者を得た。潜在的顧客における男女比は5:5であることがわかっている。しかしなにかの事情があって、調査対象者は男60人、女40人とした(男女比は6:4)。これらの対象者は、その性別のなかでは無作為に抽出されたものとみなすことにする。
いま知りたいのは、潜在的顧客(母集団)の全体における購入意向率である。その推測の手段として、調査対象者(標本)から得た回答を集計し、購入意向率を算出する。
ここでunweightedの集計値とは、「はい」と答えた人の人数を100で割った値である。
いっぽうweightedの集計値は次のように説明できる。男60人における購入意向率、女40人における購入意向率をそれぞれ求め、得られた2つの値を、母集団における割合(ここではそれぞれ0.5)で重みづけて合計する。これがweightedの集計値である。
あるいは次のようにいいかえてもよい。まず各対象者に適切な「ウェイト」を与える。たとえば、男性の対象者には5/6=0.833, 女性の対象者には5/4=1.250というウェイトを与える。次に、「はい」を1点、「いいえ」を0点とし、各対象者の持ち点にウェイトを掛けて合計し、最後にウェイトの合計で割る。これがweightedの集計値である。
さて、unweightedの集計値とweightedの集計値、どちらを使うべきか。ウェイティングすべきか、すべきでないか。
たいていの人はこう答える。ウェイティングすべきです。なぜなら、母集団における男女比が標本における男女比と異なっているので、標本から得たunweightedの集計値は、男性の回答の方向に偏ってしまうからです。
もう少し経験のある方はこう答える。確かにウェイティングすべきでない場合もあります。この例では男女だけが問題になっていますが、男女、年代、地域、などなどと複数の層が登場すると、ウェイトを算出するためのサンプルサイズが小さくなり、極端なウェイトが得られてしまい、集計値はかえって不適切になってしまうことがあります。気をつけましょう。
僭越ながら、この説明は間違っていると思う。少なくとも、ストーリーの半分しか語っていない。
私はこう答えたい。ウェイティングすべきだとも、すべきでないともいえません。
シナリオA. ウェイティングすべき場合
いくつかの架空のシナリオを考えよう。
まず最初のシナリオ。私たちは知らないのだが、実は母集団における購入意向率は、男性で0.4, 女性で0.6であるとしよう(女性の評判のほうがよいわけだ)。関心があるのは全体の購入意向率だから、つまり0.5が「正解」である。
このとき、標本における購入意向率は、男性で0.4のまわりの値、女性で0.6のまわりの値となる。標本は男性を多く含んでいるので、unweightedの集計値は男性の方向に向かって偏る。つまり、「正解」よりも少し低めになりやすい。
下の図はその様子を示したものである。
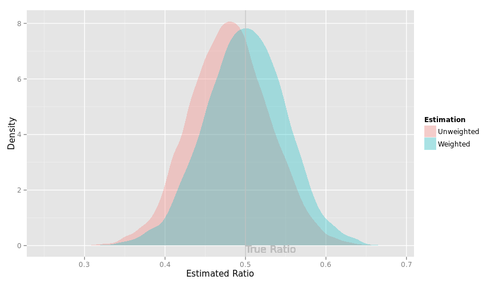
赤の山は、この架空の調査をコンピュータ上で10000回繰り返し、unweightedの集計値がどのような値をとるかを調べた実験結果を示している(微妙にデコボコしているけど、あまり気にしないでください)。赤の山の位置は、「正解」よりも少し左側にずれている。
いっぽう青の山はweightedの集計値の分布を示している。この山の真ん中(平均)は「正解」に一致する。つまり、ウェイティングによって、標本の男女比が母集団の男女比と異なることによる偏りを取り除くことができるわけである。
よかった、よかった。これがウェイティングにとってハッピーなシナリオである。私たちはウェイティングすべきだ。
シナリオB. ウェイティングすべきでないシナリオ
別のシナリオ。私たちは知らないのだが、実は母集団における購入意向率は、男性で0.5, 女性も0.5であるとしよう(購入意向は性別とは無関係なわけだ)。ここでも「正解」は0.5である。
標本における購入意向率は、男性で0.5のまわりの値、女性で0.5のまわりの値となるだろう。標本は男性を多く含んでいるけれど、男女のあいだに差がないので、unweightedの集計値は偏らない。でもweightedの集計値も偏りはしない。だから「ウェイティングしてもしなくてもよい」。と考える人が多い。
ここに落とし穴がある。このシナリオでの集計値の分布を示す。
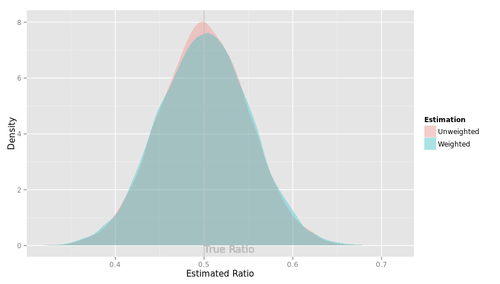
確かに、赤の山も青の山も、「正解」である0.5のまわりに分布している。でもよく見ると、青の山のほうがほんの少し、下方向につぶれて、裾の広い形になっている。つまり、unweightedの集計値に比べてweightedの集計値は、「正解」からより離れた値をとりやすい。このシナリオでは、「ウェイティングしてもしなくてもよい」のではない。ウェイティングすべきでないのである。
このように、weightedの集計値の分布は、unweightedの集計値の分布よりもばらつきが大きくなる。ウェイティングとは、集計値の分布のばらつきを犠牲にして、集計値の分布の偏りを取り除く手続きであるといえる。
シナリオC. 手に汗握るシナリオ
シナリオAは、集計値の偏りをウェイティングによって取り除くのが望ましいシナリオであった。シナリオBは、集計値に偏りが存在せず、ウェイティングによって集計値がばらついてしまう害が顕在化するシナリオであった。
では、その中間のシナリオ。母集団における購入意向率は性別によってわずかに異なり、男性で0.48, 女性は0.52であるとしよう。「正解」は0.5である。
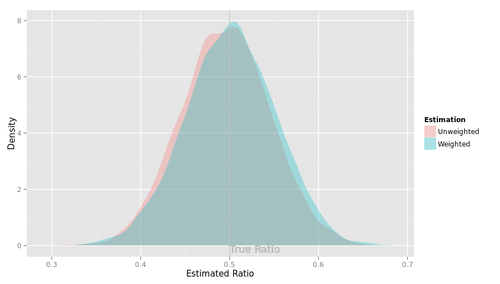
unweightedの集計値の分布は少し左にずれている。いっぽうweightedの集計値の分布は、その平均が「正解」に一致している。その代償として、分布のばらつきは少し大きい。
さて、どちらの集計値がよいだろうか？
そもそも、私たちが求める集計値とはどんな集計値だろうか。
weightedの集計値は、「正解」からみて偏りがない、すなわち、長い目で見て「正解」より大きくなりやすくも小さくなりやすくもない、という美点を持っている。いっぽうunweightedの集計値は、その分布の平均からみてばらつきが小さい、すなわち、長い目で見てその値が安定しているという美点を持っている。
でも私たちは、長い目で見て性質の良い集計値を得るために調査を行っているのではない。たった1回の調査を通じて、母集団(潜在的顧客)の性質について少しでも正しい知識を得たいと思っているのである。だから本当に重要なのは、調査によって得られた集計値が「正解」により近いことである。
上のシナリオで、集計値と「正解」0.5との差がどうなるかを計算してみよう。図でいえば、赤の山と青の山のそれぞれについて、山を形作る無数の点のそれぞれが、(その山の平均でなくて)「正解」0.5からどのくらい離れているかを調べてみる。統計学の伝統に従い、差を二乗した値を平均して表すことにする。これを平均二乗誤差という。
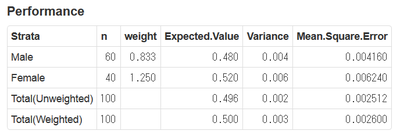
unweightedの集計値の分布は、平均0.496(男性寄りに偏っている)。分散0.002。平均二乗誤差0.0025。
weightedの集計値の分布は、平均0.5(偏りが取り除かれている)。分散0.003(すこし大きくなっている)。平均二乗誤差は0.0026。
僅差ではあるが、unweightedのほうが誤差が小さい。つまり、このシナリオでは、私たちはウェイティングすべきでない。
シナリオのマップ
これらの3つのシナリオでは、母集団の購入意向率が男女それぞれについてわかっていた。実際の調査は、母集団の性質がわからないからこそ行うわけだから、上のような図は手に入らない。
しかし、こういう図を描くことはできる。
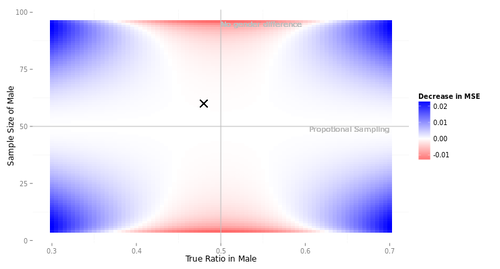
この図は、母集団の男女比は5:5, 母集団全体での購入意向率は0.5, 標本サイズは100, という3点だけを決めて描いている。
横軸は母集団における男性の購入意向率を示す。3つのシナリオでは、それぞれ横軸0.40, 0.50, 0.48であった。縦軸は男性の標本サイズを示す。3つのシナリオではすべて60であった。図中の×印はシナリオCを示している。
図中の色は、unweightedの集計値の平均二乗誤差と、weightedの集計値の平均二乗誤差との差を表している。青のエリアは、ウェイティングした方が誤差が小さい(ウェイティングすべきである)。赤のエリアは、ウェイティングしないほうが誤差が小さい(ウェイティングすべきでない)。
この図からいろいろなことがわかる。
- もし男性の標本サイズが50人に近かったら、ウェイティングしようがしまいが、集計値の性質はたいしてかわらない。考えてみれば当然である。母集団の男女比と標本の男女比がほぼ等しく、男にも女にもほぼ同じウェイトが与えられるためである。
- 男性の標本サイズが50人から離れると、ウェイティングすべきシナリオ(青)とすべきでないシナリオ(赤)が生まれる。母集団において購入意向に男女差があるときは青、ないときは赤である。
「極端なウェイト」
ウェイティングについての説明をみていると、ウェイティングの弊害として「ウェイトが極端なときは集計値の誤差が大きくなる」という点が挙げられていることが多い。この説明は当たっている面もある。上の図でいえば、ウェイト値は極端な値になるのは天井付近や床付近である。たしかに赤くなっている。
しかし、赤のエリアは天井や床だけでなく、もっと内側にも広がっている。たとえば、さきほどの3つのシナリオはすべて、ウェイトは男0.833, 女1.250であった。これを「極端なウェイト」と呼ぶのは難しいだろう。それでも、ウェイティングによって誤差が大きくなる事態は生じた。
このように、ウェイトが極端な値になるかどうかは、ウェイティングの是非にとって本質的問題ではない。
標本サイズとの関係
この図は状況によって変わる。全体の標本サイズを500に増やしてみよう。赤のエリアは小さくなってしまう。
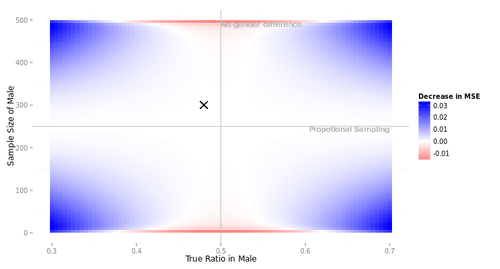
このように、標本サイズが大きいとき、weightedの集計値はunweightedの集計値に比べて有利になる。
これは次のように考えるとわかりやすいだろう。ウェイティングとは、集計値の偏りを取り除く代わりにばらつきを拡大する手続きである。集計値のばらつきは標本サイズと関係している。標本サイズが小さいときは、集計値のばらつきがもともと大きいので、ウェイティングによる拡大の影響が深刻でなる。それに対し、標本サイズが大きいときは、集計値のばらつきがもともと小さいので、ウェイティングによる拡大の影響はさほど問題にならない。
このように、ウェイティングの是非を判断する際のひとつの重要なポイントは、全体の標本サイズである。
母集団特性との関係
もっと評判の悪い製品だったらどうなるか。標本サイズを100に戻し、今度は母集団全体の購入意向率を0.2に下げてみよう。
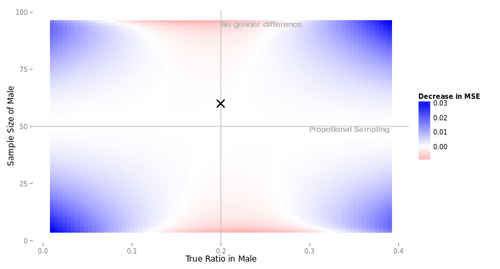
興味深いことに、赤のエリアは左右非対称になる。よくみると、男性の標本サイズのほうが大きい場合(図の上半分)、男性のほうが購入意向が高い場合にはウェイティングすべきエリアが広く(図の右上)、男性のほうが購入意向が低い場合にはウェイティングすべきでないエリアが広い(図の左上)。
これは割合という集計値の持っている性質に由来している。購入意向率とはすなわち購入意向者の割合である。割合という集計値は、真の値が0.5に近いときにばらつきが大きくなる性質を持っている。層別抽出においては、ばらつきが大きい層の標本サイズを増やしておけば、全体の集計値のばらつきを小さく押さえることができる。図の右上と左下がそれである。集計値のばらつきがもともと小さいぶん、ウェイティングにとって有利になる。
この実験からわかること
この簡単な実験から、次の点がわかる。ウェイティングすべきかどうかという問いに簡単な答えはない。
標本抽出デザインだけからは、ウェイティングすべきだともすべきでないともいえない。たとえばこんな批判を耳にすることがある。「この調査、性別と年代で均等割り付けしている調査なのに、なんでウェイトバック集計していないんだ？」 こういう非難はいささか早計に過ぎると思う。非比例の層別抽出でも、あえてウェイティングしないという判断があってしかるべきである。ウェイティングは集計値の誤差を減らすこともあれば増やすこともあるのだ。
ではどうすればいいのか
ウェイティングすべきかどうかという問いに簡単な答えはない。でも、あれこれ考えた上で、それなりの答えを出すことはできる。
上の実験から、集計値の誤差という問題について考えるための簡単なガイドラインを手に入れることができる。その調査で測定した変数のうち重要な変数(たとえば購入意向)について、次の3点に注目すれば良い。
- それらの重要な変数と、ウェイトを構成する際の層別変数(たとえば性別)との間に強い関係があるときは、ウェイティングしたほうがよい。上の例でいえば、購入意向が男女によって大きく違うときは、ウェイティングしたほうがよい。
- 集計値のばらつきがもともと大きいと考えられるときは、ウェイティングしないほうがよい。たとえば標本サイズが小さいときはウェイティングしないほうがよい。
- 調査の目的からみて、集計値の偏りよりもばらつきが問題になる場合は、ウェイティングしないほうがよい。たとえば、同じ標本抽出デザインで縦断調査(トラッキング調査)を行い、集計値の変化に注目する場合は、ウェイティングしないほうがよい。
この3つの注意点に、冒頭に挙げた3つのポイント(適切なウェイトを構成できるか、能力とやる気があるか、分析の諸前提と整合するか)を加えれば、ウェイティングの是非を判断するための材料が揃うのではないかと思う。
シミュレータつくっちゃいました
ところで、この文章を書いたもうひとつの理由、ささやかなほうの理由は...この文章で説明したシミュレーションを行うためのwebアプリを作ってしまったためである。図表はこのアプリでつくりました。
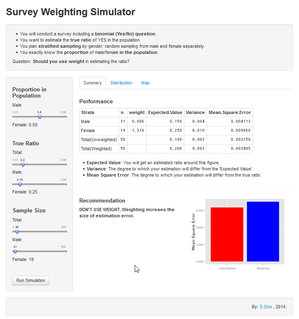URLは今後変わると思いますのでご注意ください。
Shinyというシステムの使い方を勉強するつもりで作り始めて、たった半日でできてしまった。おそろしい時代になったものだ。
ご関心あらばどなたでもお試しくださいまし。なかなか楽しいのではないかと思います。
2015/03/11 追記: アプリは停止しました。お粗末様でございました。
雑記：データ解析 - 「ウェイトバック集計」すべき場合とすべきでない場合がある(ということを説明するためのwebアプリを作ってしまった)