« 読了:de Leeuw & Mair (2009) パッケージSMACOF | メイン | 読了:Markowitz, et al.(2012) 消費者について理解すればよい製品ができるのか »
2012年11月14日 (水)
流れ流れて市場調査の会社に拾って頂いた当初,いろいろ面食らうことが多かったのだが,実験計画法? そんなのどうでもいいですよ,科学者じゃないんだから,と真顔でいわれたことがあって,このときも言葉を失った。たぶん実験ということばは,実験室やら白衣やら,おぞましくもアカデミックななにかを連想させ,人を思考停止に導いてしまうのであろう。
たとえば,調査対象者をランダムに2群に分け,一方の群にはある製品に現行のパッケージラベルを貼って提示し,他方の群には同じ製品に新しいパッケージラベルを貼って提示する。で,好意度なり購入意向を比較する。これだって立派な実験である。
ここで「パッケージラベル」を要因 factor という。登場するパッケージラベルは「現行ラベル」と「新ラベル」の二種類あるが,このそれぞれを水準 level という。つまり,このごくありふれたパッケージ・テストは,1要因2水準の実験である。
完全実施要因計画と一部実施要因計画
パッケージラベルの違いは製品への好意度に影響を与えるか。この点について推測する際には,要するに,それぞれのパッケージラベルに対して好意度を聴取し回答を集め,2グループの回答の集まりを比較すればよい。話の都合上,一方の水準について測定したこと(つまり,一方のパッケージラベルについて好意度を聴取したこと) を +1 と表現し,他方の水準について測定したことを -1 と表現することにする。
要因の数がもっと増えた場合について考えよう。たとえば,パッケージラベルの影響だけでなく,蓋の色による影響も,パッケージの形状による影響も同時に調べたい,というような場合である。3要因(A, B, Cと呼ぶ)がそれぞれ2水準を持つとすれば,水準の組み合わせは2*2*2=8個。この8個の製品をつくり,それぞれについて好意度を聴取すれば良いわけだ。以下,以下の8行の表のイメージで考えることにする。
| 製品番号 | A | B | C |
|---|---|---|---|
| 1 | -1 | -1 | -1 |
| 2 | -1 | -1 | +1 |
| 3 | -1 | +1 | -1 |
| 4 | -1 | +1 | +1 |
| 5 | +1 | -1 | -1 |
| 6 | +1 | -1 | +1 |
| 7 | +1 | +1 | -1 |
| 8 | +1 | +1 | +1 |
この表の行,つまり水準の組み合わせのことを,とりあえず製品と呼ぶことにする。英語ではラン run と呼ぶことがあるが,なんと訳せばいいのかわからない。
上の表のように,全ての属性の全ての水準の全ての組み合わせからなる全ての製品を使って実験するのが,ひとつの理想である。こういう実験計画を完全実施要因計画 full factorial design という。しかし,すべての製品を用意するのは大変だ。それに,要因の数が4つ, 5つ, ... と増えたり,2水準の要因だけではなく3水準の要因や4水準の要因が登場すると,可能な製品の数は膨大になり,そのすべてを使った実験は現実的でなくなってしまう。いくつかの少数の製品だけをうまく選び出して実験したい。これを一部実施要因計画 fractional factorial design という。
推定精度のシミュレーション
一部実施要因計画の場合,用いる製品をどうやって選べばよいだろうか。
四の五の言わずに,かんたんなシミュレーションをしてみよう。まず,「正解」を決めてしまう。好意度を7件法評定(1~7点)で聴取する場合について考えよう。各製品はある決まった好意度の高さ(「正解」)を持っている,と想定する。値はなんでもよいのだが,仮に,8製品を通じた好意度の平均は4.0ポイント,Aが-1のときよりも+1のときのほうが好意度が2.4ポイント高い,同様に B, Cではそれぞれ0.6, 0.3の差がある... ということにしよう。こうしてできた「正解」は以下の通り。
| 製品番号 | A | B | C | 正解 |
|---|---|---|---|---|
| 1 | -1 | -1 | -1 | 1.9 |
| 2 | -1 | -1 | +1 | 2.5 |
| 3 | -1 | +1 | -1 | 3.1 |
| 4 | -1 | +1 | +1 | 3.7 |
| 5 | +1 | -1 | -1 | 4.3 |
| 6 | +1 | -1 | +1 | 4.9 |
| 7 | +1 | +1 | -1 | 5.5 |
| 8 | +1 | +1 | +1 | 6.1 |
では,完全実施要因計画に基づいた架空の実験を行おう。対象者120人を8つの製品にランダムかつ均等に割り当てる。対象者には,自分が割り当てられた製品について好意度を評定してもらい,それでお役御免とさせていただく (市場調査ではこういう実験計画をモナディック・デザインと呼ぶことが多い)。各製品に対する人々の好意度はその製品が持っている「正解」の周りをばらつく,と仮定しよう。データ解析の世界でのちょっとした伝統に従い,ばらつきは左右対称なある決まった形状をとる(N(0,2)に従う)ということにしておく。
以上の仮定に従い,コンピュータ上で疑似的な回答データをつくる。現実世界と違って一瞬にしてデータが集まるので気分が良い。よくよく見ると,7件法で聴取したはずなのに回答は整数になっていないし,負の値や7以上の値も含まれているけれど,この際それは気にしないことにしよう。
得られた回答の集計結果をご報告しよう。このたびはどうも運が悪かったようで,各組み合わせに対する回答の平均は「正解」からかなりズレている。
| 製品番号 | A | B | C | 正解 | 回答平均 |
|---|---|---|---|---|---|
| 1 | -1 | -1 | -1 | 1.9 | 2.1 |
| 2 | -1 | -1 | +1 | 2.5 | 3.4 |
| 3 | -1 | +1 | -1 | 3.1 | 3.3 |
| 4 | -1 | +1 | +1 | 3.7 | 3.3 |
| 5 | +1 | -1 | -1 | 4.3 | 3.9 |
| 6 | +1 | -1 | +1 | 4.9 | 4.8 |
| 7 | +1 | +1 | -1 | 5.5 | 4.9 |
| 8 | +1 | +1 | +1 | 6.1 | 6.7 |
こうした実験を行った場合,データの分析には分散分析と呼ばれる手法を用いることが多いので,ここでもそれに従おう。主効果モデルと呼ばれる分散分析モデルを適用する(そのことの是非については,のちほど)。このモデルでは,全製品の平均, Aが+1であるときの平均に対する増加分, Bが+1であるときの増加分, Cが+1であるときの増加分,の4つをデータから推定する。以下ではこれらを「切片」「Aの係数」「Bの係数」「Cの係数」と呼ぶ。その「正解」は,4.0, 1.2, 0.6, 0.3である。
推定の結果は,それぞれ3.92, 1.16, 0.63, 0.38となった。Aの影響が過小評価され,B, Cの影響が過大評価されている。
この実験はたまたま運が悪かったのかもしれない。そこで,同じ設定の実験を10000回繰り返す。Excelなり統計ソフトウェアなりに慣れている人なら,さほど難しくはない作業だ。
各実験において,得られた4つの推定値と「正解」とのズレを調べ,10000回の実験についてズレを集計する。データ解析のちょっとした伝統に従って,ここでは推定値と「正解」の差の二乗の平均を集計値とする。推定の精度が低いほど大きな値になる。結果は... 切片0.033, Aの係数0.034, Bの係数0.033, Cの係数0.034となった。
完全実施要因計画ならば,ズレの大きさはこれくらいだ,という見当がついた。今度は,一部実施要因計画を用いて実験してみよう。あれこれ考えるのが面倒なので,片っ端から実験してみることにする。
ええと,8製品のうち7つを用いる実験計画は8パターン,8製品のうち6つ用いるなら28パターン,8製品のうち5つ用いるなら56パターン, 8製品のうち4つ用いるなら70パターン,ここまで計162パターン。さらに,8製品のうち3つなら... いや,それはさすがに虫が良すぎるだろう。実際,ちょっと考えてみればわかるのだが,各製品が持つ好意度の「正解」について予備知識がない状況で,3つの要因がもたらす影響を評価するためには,少なくとも4つの製品について調べる必要がある。
というわけで,対象者数を120人に固定したまま,8つの製品から4つ以上を用いる計162パターンのそれぞれについて,完全実施要因計画と同様に10000回の架空実験を繰り返してみる。さすがにExcelではちょっと面倒だが,なんらかの統計ソフトウェアの使用方法に慣れていれば,それほど難しい作業ではない。これをSASで試した時は,20分くらいで計算開始にこぎつけた。このたびRで書き下ろしたら,計算までに小一時間かかってしまったが,これは私が下手だからで,上手い人ならあっという間だと思う。
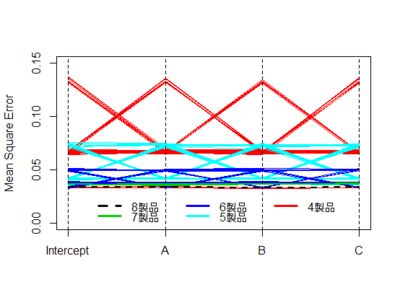
結果を上図に示す(クリックで拡大表示)。162パターンのなかには,とてもじゃないが無理,というようなパターンも登場してしまうので(例, 製品{1, 2, 3, 4}。どれもAが-1である),そのようなパターンは除外してある。
チャートの底部を水平に走る黒点線が,完全実施要因計画の場合のズレの大きさである。製品数 7 の場合のズレの大きさは,その少し上の緑色。つまり,製品を1つ減らしたせいで,「正解」からのズレが少し大きくなっている。以下,6製品, 5製品, 4製品と,製品数を減らすにつれてズレがますます大きくなることがわかる。
。。。いや,ちょっと待て! チャートの底部をよく見てほしい。目をこらすと,ああ,なんということだろうか! 黒点線の周りに,かすかな赤い輝きがみえるではないか!!
直交計画の威力
わざとらしい驚き方で恐縮だが,実は製品数4の一部実施実験計画のなかに,たったふたつだけ,完全実施要因計画に匹敵する推定精度を誇る,特別なパターンが存在するのである。それは,製品{1,4,6,7}(下表のアミカケ部分)を用いる計画,そしてその残りの製品{2,3,5,8}を用いる計画である。
| 製品番号 | A | B | C |
|---|---|---|---|
| 1 | -1 | -1 | -1 |
| 2 | -1 | -1 | +1 |
| 3 | -1 | +1 | -1 |
| 4 | -1 | +1 | +1 |
| 5 | +1 | -1 | -1 |
| 6 | +1 | -1 | +1 |
| 7 | +1 | +1 | -1 |
| 8 | +1 | +1 | +1 |
このふたつの実験計画はなぜ特別なのか。上の表のアミカケ部分をよくみると,このふたつの実験計画は次の2つの特徴を備えていることがわかる。
- A,B,Cのどれをみても,+1と-1が2行ずつはいっている。つまり,ある要因のなかで,各水準を持っている製品数が水準間で同じである。この性質を,釣り合いが取れている balanced という。
- たとえば要因AとBを取り出してみよう。Aが-1のとき,Bは-1がひとつ,+1がひとつである。Aが+1のときも,Bは-1がひとつ,+1がひとつである。つまり,どの2要因を取り出しても,「一方が+1だったら,そうでない場合に比べて,他方は+1になることが多い(少ない)」という関連性がない。この性質を直交している orthogonal という。
少々ヤヤコシイのだが,この2つの性質を同時に兼ね備えた実験計画のことを特に直交計画 orthogonal design という。ここでいう「直交」とは,さきほどの「直交」とはちょっと別の意味で用いられている(計画行列における直交性を指している)。
考えてみれば,これは不思議な話だ。私たちはいま,いくつかの製品についての消費者の好意度の回答を集め,それを分析することで,好意度の背後にあるメカニズムを探ろうとしている。だったら,調べる製品の数は多ければ多いほうがよい,と考えるのが自然であろう。しかし実際には,製品の選び方にはコツがあり,多ければ良いとは限らないのである。
ね? 実験計画法って必要でしょう?
主効果と交互作用
うまい話には大抵裏がある。直交計画の推定精度にも,それ相応の代償が伴うのだけれど,その話の前に,まず直交計画の性質について紹介しておこう。
話をいったん完全実施要因計画に戻す。たいていの場合,私たちは個々の要因が好意度にどの程度影響しているかを知りたい。たとえば,要因Aの2つの水準のあいだで,好意度にどのくらいの差が生じるかどうかを知りたい。これを要因Aの主効果 main effect という。その推測に際しては,Aが+1である4製品に対する好意度の集まりと,-1である4製品に対する好意度の集まりを比較すればよい。
しかし,世の中は時としてわれわれが期待するよりも複雑に出来ている。私たちがそれを知りたいかどうかは別にして,現実には,「要因AとBが両方+1だったときにのみ好意度が高くなる」... というような影響が生じているかもしれない。これを要因Aと要因Bの交互作用効果 interaction effect という。その推測に際しては,A列とB列の符号が合致している4行と,符号が異なっている4行を比較すればよい。
直交計画の分解能
交互作用効果の早見表をつくるつもりで,A列とB列を掛けた列(AB列)を表に追加しておこう。AとBの交互作用をチェックしたいときは,AB列が+1である4行と-1である4行とを比較すればよい。ついでに,「要因1と3の交互作用」(AC列),「要因2と3の交互作用」(BC列),「要因1,2,3の交互作用」(ABC列) も作っておくことにしよう。こうしてできた表は,実験計画法の世界でL8直交表と呼ばれる有名な道具となる。
| A | B | C | AB | AC | BC | ABC |
|---|---|---|---|---|---|---|
| -1 | -1 | -1 | +1 | +1 | +1 | -1 |
| -1 | -1 | +1 | +1 | -1 | -1 | +1 |
| -1 | +1 | -1 | -1 | +1 | -1 | +1 |
| -1 | +1 | +1 | -1 | -1 | +1 | -1 |
| +1 | -1 | -1 | -1 | -1 | +1 | +1 |
| +1 | -1 | +1 | -1 | +1 | -1 | -1 |
| +1 | +1 | -1 | +1 | -1 | -1 | -1 |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 |
さて,話を一部実施要因計画に戻そう。さきほどみつけた直交計画とL8直交表を見比べると,L8直交表でABC列が+1である4行,ないし-1である4行を抜き出したのが,さきほどの直交計画であることがわかる。いいかえれば,さきほどの直交計画をつくるためには,L8直交表でABC列が+1ないし-1である行を抜き出せばよい。つまりこの例で,ABC列は「ありうる製品のうち,一部実施計画に取り入れるべき製品はどれか」を表していることになる。
この「ABC」をこの一部実施要因計画のジェネレータ generator という。また,ジェネレータの桁数を分解能 resolution と呼ぶ。なぜかわからないがローマ数字で書く習慣がある。さきほどの直交計画は分解能IIIと呼ばれる。英語でいうとかっこいいですね。自分がなにかすごくつまらない仕事をしているのではないかと気がめいるときは、小声で「よし、レゾリューション・スリーで実験だ」などと呟けば、すこしは虚栄心が満たせるかもしれない。
分解能IIIの直交計画,その欠点と役割
分解能IIIの直交計画にはある深刻な欠点がある。もう一度,よくみてみよう。
| 製品番号 | A | B | C |
|---|---|---|---|
| 1 | -1 | -1 | -1 |
| 2 | -1 | -1 | +1 |
| 3 | -1 | +1 | -1 |
| 4 | -1 | +1 | +1 |
| 5 | +1 | -1 | -1 |
| 6 | +1 | -1 | +1 |
| 7 | +1 | +1 | -1 |
| 8 | +1 | +1 | +1 |
アミカケされた4行では,Aが-1である2行ではBとCの符号が異なり,Aが+1である2行ではBとCの符号が一致している。
つまりこういうことだ。仮に,実験の結果Aが+1である2製品に対する好意度の集まりが,Aが-1である2製品に対する好意度の集まりよりも高かったとしよう。それは「Aによって好意度が変わる」ことを意味しているのかもしれないし,「BとCの組み合わせによって好意度が変わる」ことを意味しているのかもしれない。つまり,Aの主効果を意味しているのかもしれないし,BとCの交互作用効果を意味しているのかもしれない。
このように,分解能IIIの直交計画では,Aの主効果とBCの交互作用効果を区別して捉えることができない。同じことが,Bの主効果とACの交互作用効果の間にも,Cの主効果とABの交互作用効果の間にもいえる。
さきほどのシミュレーションでは,データに主効果モデルと呼ばれる分散分析モデルを適用した。つまり,主効果のみ推定するモデルである。本来,交互作用効果があるかどうかわからない状況下では,交互作用効果に関心があろうがなかろうが,交互作用効果の推定も行うべきである。交互作用効果が存在するのに,それを無視したモデルを使ってしまうと,誤った知見が得られてしまうかもしれないからだ。
しかし,分解能IIIの直交計画で得たデータでは,そもそも主効果と交互作用効果を切り分けられない。分散分析では主効果モデルしか使えない。得られた主効果の推定値がほんとに主効果を表しているのかどうかは,分析者の解釈に任されている。3要因の主効果をたった4製品で精度よく推定できることの,これが代償である。
いや,そういう言い方は後向きですね。もっとポジティブに言い直せば,こうだ。いま,測定値に影響しそうな要因がたくさんあるんだけど,どれが影響しているのかわからない,としよう。そんなときは,思いつく要因を片っ端から組み込んだ実験をやって,影響がありそうなものを選び出すことができたら便利である。そんな場合は,とりあえず交互作用効果は無視して,主効果だけに注目するという作戦が有用であろう。分解能 III の計画は,そんな場面で役に立つ。
最適計画への道
さて,上のアイデアは,完全実施要因計画で必要とされる膨大な数の製品のなかから,釣り合いと直交性を保ったまま現実的な数の製品をうまいこと選び出すというアイデアであった。
ところが実際には,要因の数や水準の数が多くなると,完全実施要因計画の製品数は膨大になる。そこから少数の製品を抜き出すと,釣り合いと直交性がどうしても崩れてしまうことが多い。どうしたらよいか?
さきほど試したような簡単なシミュレーション実験を行い,推定精度が相対的にましな計画を選べばよい,というのがひとつの答えである。しかし,ありがたいことに,分散分析のような線形モデルがさまざまな実験計画のもとで持つ推定精度は,数理的に単純な一定の性質を持つことが分かっている(パラメータの推定量の共分散行列は情報行列の逆行列に比例する)。それによれば,推定精度がもっともよいのは完全実施要因計画ないし直交計画であり,釣り合いが崩れたり直交でなくなったりするにつれて推定精度が下がっていく。その低下の程度も簡単に計算できる。
そこで,直交計画が作れない場合にも,実現可能な範囲内でもっとも推定精度のよい実験計画を探そう,という考え方が登場する。こういうアプローチを最適計画 optimum design という。完全実施要因計画のときに100%となるような推定精度の指標を使い,なるべく100%に近い一部実施実験計画を探そうというわけである。大変な作業だが,コンピュータが一瞬にして良い答えを出してくれる。推定精度を測る指標にはいくつかあるが,D-最適性という指標が用いられることが多い(この指標は,情報行列の逆行列の固有値の幾何平均の小ささを表す)。
面白いことに,釣り合いの崩れ方のちがいのせいで,要因が直交している計画よりも直交していない計画のほうがD-最適性が高くなったりすることがある。そのせいで,実験計画法の教科書の説明どおりに丁寧に計画するより,専用のソフトを使って力づくで作ったほうが,良い計画ができることがある。
市場調査の教科書をみると,実験計画の初歩的概念は紹介してあるし,直交計画について説明している親切な教科書もある。でも,ソフトウェアでの実験計画作成や,D-最適性について説明している本は見かけない。他の分野では常識となっている話なのに,なんでですかね? もっと普及してよい考え方だと思う。
最適計画の使い道
もちろん,実験計画の良し悪しは,あるひとつの基準だけで決められるものでもない。たとえば,交互作用効果を無視した実験ではあるものの,あとでこっそり交互作用の有無もチェックしたい,といったこみいった裏の事情がある場合も珍しくないだろう。D-最適性が多少低くなってもいいから,釣り合いが崩れているのだけは困る,とか。どうしても実現が難しい製品があるとか。どうしてもこの製品を入れたいとか。現実は常に多様である。
それに,ここまでの話はすべて,データのサイズが一定で,用いる製品数だけが変えられる,という場合の話である。実際には,製品数が増えればデータサイズも増える場合が多いだろう(各対象者に全製品を提示する場合とか)。その場合は,もちろんデータサイズが大きくなった方が推定精度は向上する。しかし,用いる製品数の増加は,実験にかかる時間やコストの増大を意味したり,対象者の疲労や回答の質の低下につながるかもしれない。いろいろな事情が複雑に絡み合い,もはやD-最適性どころの騒ぎではない。実験の設計はどうしたって,複数の条件を睨みながら考える複雑な意思決定プロセスなのだ。
というわけで,一部実施要因計画をつくる際のお勧めはこうだ。リサーチャーが残業して,手作業で必殺の実験計画をひとつだけ作り込むのは,もうやめよう。さっさと実験計画用のソフトを買い,さまざまな設定の下の実験について、実験計画のいくつかの候補をつくってしまえばよい。何個でも一瞬にして作れるし、追加料金はかからない。で,それぞれの候補について,D-最適性や,その場で求められているさまざまな特性についてチェックし,一番ましな奴を選ぶ。という手順が,よろしいのではないかと思います。
Postscript
ずいぶん前に,当時の同僚からもらった質問に応じて書きかけていた返事が,途中で放ってあったのをみつけた。捨ててしまうのもなんなので,具体的な業務と関わる部分を削って,ブログに書き留めて供養とする次第である。これを読んだ誰かが,私の愚かな誤りを見つけて馬鹿にするかもしれないが,それはまあ,そのときである。
要因計画を用いた製品テストなんて市場調査の世界では稀だ,とおっしゃる方がいらっしゃるかもしれない。そのような,良く言えば現実力旺盛な方(悪く言えば想像力を欠いた方)のためには,たとえばBIBDによる製品テスト,応答曲面モデルによる最適化,そして離散選択型コンジョイント分析といった,市場調査においてもっとおなじみの場面においても,最適計画というアイデアがきわめてパワフルであることを示せばよいのだが,ちょっと気力が尽きました。
本稿の種本はKuhfeld, Tobias & Garrett (1994, J. Mktg. Res.),岩崎(2006)「実験計画法」,などだが,どれもきちんと読んで理解しているとは言い難いので,すべての誤りの責任はもちろん私にあります。
雑記:データ解析 - 実験計画の最適性について (お問い合わせに答えて)