読書日記

« 2013年4月 | メイン | 2013年6月 »

2013年5月31日 (金)

女子攻兵 02 (BUNCH COMICS) [a]
松本 次郎 / 新潮社 / 2012-07-09
女子攻兵 03 (BUNCH COMICS) [a]
松本 次郎 / 新潮社 / 2013-04-09
舞台は近未来、兵士たちは巨大ロボットに搭乗して血みどろの戦いを繰り広げているのだけれど、その巨大ロボットはなぜか女子高生の姿をしていて、兵士たちはやがて静かに狂っていく... という、大変奇妙な設定のマンガ。どうやら「地獄の黙示録」のような話になるようだ。

ひきだしにテラリウム [a]
九井諒子 / イースト・プレス / 2013-03-16
ファンタジックなショートショート集。とても面白い。。。

リューシカ・リューシカ(6) (ガンガンコミックスONLINE) [a]
安倍 吉俊 / スクウェア・エニックス / 2013-04-22
幼児の視点から日常世界を描くコメディ。これはこれで良いマンガだと思うのだけれど、傑作「よつばと！」とどうしても比較されてしまうだろう。運が悪いなあ。

銀の匙 Silver Spoon(7) (少年サンデーコミックス) [a]
荒川 弘 / 小学館 / 2013-04-18

ストレニュアス・ライフ (ビームコミックス) [a]
丸山 薫 / エンターブレイン / 2011-06-15

病室で念仏を唱えないでください 1 (ビッグコミックス) [a]
こやす 珠世 / 小学館 / 2013-04-30
こういう種類のマンガをなんと呼べばいいのかしらん。。。心温まるヒューマンドラマ、兼、専門分野の知識が詰め込まれた情報マンガ。要するに、いかにも小学館「ビッグコミック」に載っていそうなマンガであった。こういう作品を安定的に産み出していくノウハウがあるんだろうなあ。それはそれで凄いことだ。

コミックス(2011-) - 読了：「女子攻兵」「ひきだしにテラリウム」「リューシカ・リューシカ」「銀の匙」「ストレニュアス・ライフ」「病室で念仏を唱えないでください」

オールラウンダー廻(11) (イブニングKC) [a]
遠藤 浩輝 / 講談社 / 2013-05-23
いわゆる超人は出てこない、地味な格闘技マンガなのだけれど、不思議に面白い。良いマンガだなあ。

ラブやん(17) (アフタヌーンKC) [a]
田丸 浩史 / 講談社 / 2012-07-23

花咲さんの就活日記 2 (IKKI COMIX) [a]
小野田 真央 / 小学館 / 2013-04-30

カブのイサキ(6)<完> (アフタヌーンKC) [a]
芦奈野 ひとし / 講談社 / 2013-01-23
雑誌連載で読んでいたのだけれど、結末がよく理解できなかった。単行本で読んだらわかるのかな、と思っていたのだが、やはりわからなかった。どういういきさつだったのだろうか。あれこれ深読みする楽しみ方もあるのかもしれないけれど。。。

ZUCCA×ZUCA(5) (KCデラックス モーニング) [a]
はるな 檸檬 / 講談社 / 2013-04-23

犬神姫にくちづけ 2巻 (ビームコミックス) [a]
宮田紘次 / エンターブレイン / 2013-04-15

千年万年りんごの子(2) (KCx(ITAN)) [a]
田中 相 / 講談社 / 2013-05-07

87CLOCKERS 3 (ヤングジャンプコミックス) [a]
二ノ宮 知子 / 集英社 / 2013-05-10

コミックス(2011-) - 読了：「カブのイサキ」「オールラウンダー廻」「花咲さんの就活日記」「ラブやん」「犬神姫にくちづけ」「千年万年りんごの子」「87 CLOCKERS」

2013年5月19日 (日)

　このブログを書き始めてからずいぶん経つが、所詮は自分のための備忘録に過ぎない。いちばん熱心な読者はたぶん私だ。書店の棚に平積みになっている連載マンガのこの巻を、俺はもう読んだだろうか？ と疑問に思った際、このブログはとても重宝する。店頭でスマフォと格闘している姿は、あまり格好のよいものではないけれど。
　そもそも私には世の中に訴えたいことが特にない。とりたてて語るべき知恵もない。アクセスログを調べると、過去のいくつかの記事が予想外に多くの方に読まれていることに驚くが(片側検定について書いた記事とか)、もっときちんとした専門家がお書きになったものをご覧いただいたほうが良いわけで、少し申し訳なく思っている。

　これから書くのは、このブログを書き始めて以来ほとんどはじめて、純粋に自分以外の誰かのために載せる記事だ。特に、検索エンジン経由でたどり着く方に向けて載せる記事だ。
　振り返ってみると、私は何年か前から、だいたい年に数回のペースで、以下の内容をどなたかに説明している。聞き手にとっては面倒で退屈な内容だ。説明に成功することもあれば失敗することもある。偉大なるインターネットの力によって、説明の回数を減らし成功率を上げたい。
　というわけで、ずっと前にお問い合わせに応じて書きためていた文章を載せておくことにする。どうかこの記事が、正しい内容を正しいやりかたで説明していますように。そしてgoogleの検索結果の上の方に出てきますように。

　以下の内容はとても単純である。たった一言で要約できる。

　統計ソフトがいう「ウェイト」は、調査でいう「ウェイト」ではない。

　もう一度書きます。SPSSとかSASとか！そういう統計ソフトの！ ウェイトとか重み付けとかっていうのは！ 調査でいうところの！ いわゆるウェイトのことではないです！
　。。。このくらい大声で書いておけば、検索されやすくなるだろうか。

調査における「ウェイティング」

　市場調査の会社にお世話になって驚いたことのひとつは、結果の集計に際してウェイティング(確率ウェイティング)を実に良く使う、ということである。親の仇かというくらいによく使う。

　確率ウェイティングとはこういう話だ。
　ある集団の性質について調べるため、その集団に属する人を対象に調査を行った。調査対象者がこの集団を互いに独立に偏りなく反映していると仮定し、得られたデータから統計的推測を行いたい。
　さて、私たちはこの集団(対象母集団)における男女比が5:5であると知っている。しかしなにかの事情によって、調査対象者の男女比は7:3にならざるを得なかった。この事情にはいろんな種類がありうるが、たとえば調査設計時の事情が考えられる(比例割当でない層別抽出)。

　この調査対象者の回答をそのまま集計し、平均や割合を求めてしまうと、その値は男の回答をより強く反映してしまい、母集団の推測としては歪んだ値になってしまう。
　これを避けるために、男の回答には小さな重み(ウェイト)、女の回答には大きな重みを与えて集計する。これが調査でいうところのウェイティング、すなわち確率ウェイティングである。
　なお英語では、probability weighting, survey weighting, sampling weightingなど、いろいろな呼び方が用いられている。検索するときに困る。

　市場調査の業界団体である日本マーケティング・リサーチ協会がまとめた「マーケティング・リサーチ用語辞典」を見ると、「ウェイトつき集計」という項で確率ウェイティングが説明されている。市場調査に限らず、広義の社会調査全般において、ウェイト、ウェイティング、ウェイト・バックという言葉は確率ウェイティングを指して使われることが多いと思う。

確率ウェイティングと拡大推計

　確率ウェイティングは拡大推計とごっちゃにして語られることもある。

　たとえば、前掲の業界団体による市場調査会社向けガイドラインには、ウェイティングについての注意点を挙げている箇所がある。

一般的にウエイトバックが必要となる理由は
1. 層化サンプリングの段階でウエイト付けする場合
2. 回収率の違いにより標本構成に偏りが出てそれをウエイト付けにより補正する場合
上記2点が多いと考えられるが、[中略] ウエイト付けをした場合、主な表すべてにおいて、ウエイト付けした基数（ベース）としない基数（両者を明確に区別）を明示すること。

前半はどうみても確率ウェイティングに関する説明である。ところが後半では、「ウェイト付けした基数」という文言が登場する。ウェイティングしようがしまいが標本サイズは標本サイズなのであって、これは意味不明である。

　実は、「1000人の対象者のうち3000人がこの製品を買いたいと答えた、市場には潜在顧客が1000万人いるから、発売すればきっと300万人が買ってくれるだろう」というような単純な拡大推計を指して「ウェイティング」ということもある。
　ガイドラインの文言は、確率ウェイティングと拡大推計の両方について同時に述べているようである。

　確率ウェイティングは標本の性質に応じて必要となるもので、あらゆる統計的分析に影響する。いっぽう、拡大推計は標本の性質とは無関係に要請され、要約統計量のなかでも合計にしか影響しない。クロス集計の手順のみについて考えれば似たようなものかもしれないが、このふたつは分けて考えたほうが良いと思う。

ウェイティングした分析はできますか？

　調査データの分析において確率ウェイティングはどんなときに必要か。仮に必要だとして、ウェイトはどうやって求めるか。
　これはなかなか難しい問題で、容易な答えはない。悩みの種である。あまりに悩んだ末、高名な専門家による解説を全訳してしまったことさえある。若気の至り、窓の雪。しかしその話は脇に置いておく。

　本題は、確率ウェイティングのためのウェイトが各ケース(ローデータの行)に対してすでに付与されているとき、そのウェイトを用いながらさまざまな統計的推測を行うことができるか、という点である。つまり、統計ソフトを使い、データに確率ウェイティングを行いつつ、差の検定を行ったり、相関を求めたり、回帰分析や因子分析を行ったりすることができるか(行うべきかどうかは別にして)、という点である。

　私は繰り返し説明してきた。できません。十中八九できません。なぜなら、お使いの統計ソフトがいうところの「ウェイト」は、私たちが思っているような意味でのウェイトではないからです。

手計算による確率ウェイティング

　ごく簡単な例について考えよう。
　母集団における男女比は5:5。事情があって、標本における男女比が7:3となるように設計した。母集団は十分に大きいものとする。非現実的ではあるが、標本サイズは男7, 女3, 計10であるとしよう。
　この10人が、ある変数について次のような値を持っている。

男性	1, 2, 2, 3, 3, 4, 4
女性	1, 2, 3

　このデータに基づき、母集団におけるこの変数の平均(母平均)について推測したい。

　まずは、統計ソフトを使わずに考えてみよう。ひとまず男性に注目する。標本平均は、(1+2+2+3+3+4+4)/7=2.714。つまり、母集団における男性の平均は2.714と推定される。
　この推定はどのくらいあてになるだろうか。標本平均の分散を求めよう。統計学の初級の教科書に書いてあるように、標本平均の分散は (不偏分散)/(標本サイズ) である。ええと、不偏分散は1.238, 標本サイズは7 だから、標本平均の分散は1.238/7=0.177だ。
　同様に女性についても電卓を叩いてみると、標本平均は2.000, 標本平均の分散は0.333である。

　では、全体の平均について考えよう。いま、男性の平均が2.714、女性の平均が2.000と推定されていて、かつ母集団のうち男性は5割、女性は5割であることがわかっているのだから、男女をあわせた平均は 2.714*0.5 + 2.000*0.5 = 2.357 と推定できる。
　この推定はどのくらいあてになるか。推定量の分散は、{(男の標本平均の分散) * (男の割合)^2 + (女の標本平均の分散) * (女の割合)^2} となる (ご不審の向きは、L. Kish "Survey Sampling"(Wiley) の80-82頁、豊田秀樹「調査法講義」(朝倉書店) の131-132頁をご覧ください)。ええと、0.177*0.25 + 0.333*0.25 = 0.128である。

　以上が「正解」である。表にまとめておく。なお、標本平均の分散の平方根は標準誤差と呼ばれ、広く用いられているので、それも添えておく。

	母平均の推定値(標本平均)	その分散	標準誤差
男性	2.714	0.177	0.421
女性	2.000	0.333	0.577
全体	2.357	0.128	0.357

手計算による確率ウェイティング(ケース・ウェイトを用いて)

　この計算を、個々のケースにウェイトを与える形で表現しなおしてみよう。

　まず、各ケースにウェイトを与える。このウェイトは、ケースが母集団から抽出される確率の逆数に比例した値であればなんでもよいのだが、一番わかりやすいのはこういう求め方だ。母集団における男の割合は5割、標本では7割だから、男のウェイトは5/7=0.714。同様に、女のウェイトは5/3＝1.667。ウェイトの合計は10となる。

　母平均の推定値、すなわち「ウェイティングされた標本平均」を求める際には、個々の値にウェイトを掛けながら合計し、ウェイトの合計で割る。{1*0.714 + 2*0.714 + ... + 2*1.667 + 3*1.667) / 10 = 2.357。
　上記の結果とぴったり一致する。計算式を変形しただけだから、当たり前である。

SPSSで試してみると

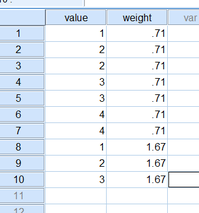
　では、統計ソフトを使って試してみよう。みんな大好きな IBM SPSS Statistic での例を紹介する (ver.19で試しました)。下図のデータを用意する。クリックすると大きくなるはずです。

SPSSのメニューには[データ]-[ケースの重み付け]という機能がある。こいつはきっと確率ウェイティングの機能にちがいない、というわけで、「ケースの重み付け」を選び、変数weight を指定してみよう。次に、[分析]-[グループの平均]で変数valueの平均を求める。[オブション]で「平均値の標準誤差」を選んでおく。アウトプットは...

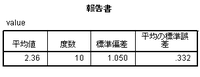
　平均値は2.357。「正解」と一致する。ところが、平均の標準誤差は0.332。「正解」よりも少し小さい。

　平均の標準誤差なんてどうでもいいです、などというなかれ。たいていの推測統計手法は標準誤差と関係している。みんなが死ぬほど大好きな検定だって、もちろんそのひとつだ。標準誤差が誤りなら、検定の結果だって誤りだ。これはとても大事な話なのである。

頻度ウェイティング

　なぜこのような結果になるのか。理由は拍子抜けするほどに簡単だ。
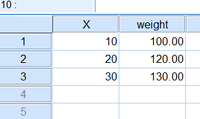
　SPSSでいう「ケースの重み付け」は確率ウェイティングのことではない。それは単に「ウェイトの数だけこのケースをコピーしてくれ」ということである。

　たとえば上の3行のデータを与え、変数weightで「ケースの重み付け」を行うと、SPSSはこう考える。変数Xが10である行が100行、20である行が120行、30である行が130行、全部で350行のデータなんですね、わかりました、と。

　こうした機能は「頻度ウェイティング」と呼ばれることがある。頻度ウェイティングはデータ行列のサイズを小さくするための工夫に過ぎない。

　頻度ウェイトによってコンパクトに表現されたデータ行列を一発で扱う方法について考えてみよう。ある変数の標本平均を求める際には、個々の値に頻度ウェイトを掛けながら合計し、頻度ウェイトの合計で割ればよい(なぜなら、頻度ウェイトは本来のローデータにおけるケース数だから)。
　この式は、幸か不幸か、確率ウェイティングのもとで母平均の推定値を求めるための式と、た・ま・た・ま、同じ形になっている。そのせいで、SPSSがウェイトを頻度ウェイトとみなして求めた標本平均は、同じウェイトが確率ウェイトだった場合の母平均の推定値 2.357 と、た・ま・た・ま、一致する。だからといって、SPSSが確率ウェイトを正しく扱えるわけではない。

　なお、SPSSにとってはウェイトは頻度なのだから、それは整数でないとおかしい。さきほどはウェイトとして整数でない値を与えたが、よくもエラーにならないものである。実際、上記で試した[分析]-[グループの平均]は、整数でないウェイトをむりやり頻度として捉えるが、他の機能は、ウェイトを整数に丸めてしまったり、そもそも無視してしまったりすることがあるらしい。

分析ウェイティング

　もうひとつの有名な統計ソフトであるSASでは、また少し話が違う。
　SASでは各プロシジャのweight 文でケース・ウェイトを指定できる。その扱いはプロシジャによっても設定によってもちがうのだけれど、通常は、「このデータの行はサブグループの平均を表していて、それぞれのグループのサイズがウェイトで表されているのね」という意味に解される。

　たとえば、さきほどの3行のデータをSASに与え、weight列をケース・ウェイトに指定すると、通常は次の意味になる。「サブグループ1はサイズ100, Xの平均は10だった。サブグループ2はサイズ120, Xの平均は20だった。サブグループ3はサイズ130、Xの平均は30だった。」
　こうしたウェイティングは「分析ウェイティング」と呼ばれることがある。これもまた、確率ウェイティングではない。

統計ソフトにおける「ウェイティング」とは

　統計ソフトの中には確率ウェイティングを扱うことができるものもある。

• SASのsurveymeanプロシジャは、複雑な標本抽出によるデータのために特に用意されているプロシジャで、確率ウェイトを正しく処理することができる。先ほどのサイズ10のデータをsurveymeanプロシジャに与えると、全体の平均は2.357, 標準誤差は0.357、手計算による「正解」とぴったり一致する。
• SPSS StatisticsにはComplex Samplesというパッケージが用意されているらしい。別料金で。
• 経済統計の分野で有名なStataは、与えたウェイトが確率ウェイトなのか頻度ウェイトなのか分析ウェイトなのかを指定できるそうである。
• Rにはsurveyというパッケージがある。
• 公的調査の分野ではSUDAANというソフトが有名である。検索すると茨城県大洗町の割烹「寿多庵」が引っかかるので困ってしまう。あんこう鍋がおいしいらしい。
• 構造方程式モデリングのソフト Mplus は確率ウェイティングに対応している。
• 最後に、世の中には調査データのクロス集計だけに特化した業務用ソフトというものがあって、それらのソフトは、(これも長い話になるのだが)基本的には、確率ウェイティングを伴う検定を正しく行うことができる模様である。

　そういうソフトでないかぎり、お使いの統計ソフトでは ... もっと具体的にいえば、SPSS Statistic BaseならびにAdvanced Statistics、SAS/BASEならびにSAS/STATのsurvey系プロシジャを除く全プロシジャ、その他もろもろの統計ソフトでは ... 確率ウェイティングを伴う分析を行うことはできない。メニューに「重み付け」という機能があっても、プロシジャにweight文というのがあっても、それは確率ウェイティングではない。

　考えてみれば、統計ソフトのユーザは多方面にわたるが、確率ウェイティングをしたいと思う人はせいぜい市場調査・社会調査の関係者くらいであろう。一般的な統計ソフトのメニューにある「重み付け」が、調査実務家の考える意味でのウェイティングでないとしても、文句をいえる筋合いではない。

　ややこしいのは、確率ウェイティングに対応していないソフトに誤って確率ウェイトを与えて要約統計量を求めたとき、平均と割合だけは期待通りの値が出力されることがある、という点である。繰り返しになるが、それはた・ま・た・まである。他の結果は誤っている。
　統計ソフトがいう「ウェイト」は、調査でいう「ウェイト」ではない。

あえて教訓を求めるならば

　最初に書いたように、私には世の中に訴えたいことは特にない。とりたてて語るべき知恵もない。ただ単に、日頃繰り返している説明を文章にしておき、仕事を楽にしたいだけである。
　しかし、あえて教訓らしきものを引き出すとすれば、こういうことはいえる。

　私の説明にオリジナリティはない。webを探せば、もっとわかりやすい説明がみつかる。たとえばこちらやこちら。統計ソフトのアウトプットをこまかーく調べた面白い研究もある(PDF)。
　さらに、SPSS Statisticsを起動し[ケースの重み付け]ダイアログの[ヘルプ] ボタンを押すと、次の説明が現れる。

[ケースの重み付け] では、統計分析を行うため (複製をシミュレートすることにより) ケースに異なる重みを付けることができます。重み付け変数の値は、データ ファイル内の 1 つのケースが表す観測数を示していなければなりません。

いささか不親切ではあるけれど、簡にして要を得た説明である。この記事で長々と書いてきたことはすべて、ソフトのマニュアルに、はっきりと書いてあることなのだ。

　にもかかわらず、推定や検定やもっと複雑な統計的分析の際に、SPSS Statisticsの[ケースの重み付け]で確率ウェイティングを行おうとしている方に、私はこれまでたくさん出会ってきた。それはもう、びっくりするくらいにたくさん。そのなかには、すごく優秀な分析者もいらっしゃったし、調査実務に携わって何十年というベテランの方もいらっしゃった。

　というわけで、教訓はこうだ。実務家の豊富な経験なるものは、必ずしもあてにならない。統計ソフトの使い方を先輩に教わったり、誰かの書いたブログを読んでいる暇があったら、そのソフトのマニュアルを読んだほうがよいのではないかと思います。

雑記：データ解析 - 統計ソフトの「ウェイト」は調査の「ウェイト」ではない

2013年5月 7日 (火)

Tadajewski, M., (2006) Remembering motivation research: Toward an alternative genealogy of interpretive consumer research. Marketing Theory, 6(4), 429-466.
　たまたま市場調査の会社にお世話になったせいで、仕方がないからまあその方面の教科書などを読んだりしたわけですが、どの分野でもそうであるように、本に書いてあることと実際のビジネスとはちょっとズレがある。たとえば、市場調査の教科書にはモチベーション・リサーチについての記載は少ないし、消費者行動論の教科書でも過去の歴史的遺産扱いだが、実際の調査ビジネスでは現役だと思うんですけどね。コカ・コーラのブランド管理の話などは有名であろう。フロイトとユングに由来する普遍的な消費者理解システム、なあんていう調査パッケージを売っている会社だっていくつかある。
　このズレはどこから出てくるんだろうなあ、と前に不思議に思ったことがあって、そのときに読みかけて数ページで挫折した論文。モチベーション・リサーチの歴史を辿るという酔狂な内容。
　英語がやたらに回りくどいし、妙にペダンチックなので、全然頭に入らない。整理の都合上読み終えたことにしておくけど、勘弁してほしいよ、もう... みんなが英語が達者というわけじゃないんだから...
　いくつかメモ:

• モチベーション・リサーチはErnest Dichterがつくったものだとみなされていることが多いが、実際にはDichterの渡米の前に、すでにPaul Lazarsfeldによって種がまかれていた(おおっと、マスメディア限定効果説の人ではないか。消費者行動論の偉い人でもあったのか)。ある意味、モチベーション・リサーチの立役者はウィーンの政治状況だったといえる。当時オーストリアの保守党政権は社会主義者を弾圧し、ラザーズフェルドの家族は投獄されていたし、ディヒターはユダヤ人亡命者だった。
• ディヒターは自分はフロイディアンではない、もっと折衷主義的だ、と述べていたそうだ。ふうん。
• モチベーション・リサーチは膨大なインタビューと観察を通じて、消費者行動の背後にある主題的連関を探そうとするのだけれど(「インスタント・コーヒーの消費者は怠け者だと思われている」とか)、みつけたパターンを法則として一般化するのではなく、ひたすらその検証を続けていく。また、観察は誤りうるが直接的であり理論中立的であると考えられている。そういう点では、論理実証主義とちょっと似ているところがあった、とかなんとか。ふうん。
• ディヒターはちょっと大言壮語するところがあって、モチベーション・リサーチはそのせいで支持を失った面があるのだそうだ。さらに、50年代の赤狩りのなかで、研究助成が非政治的な定量的研究に向けられるようになったのも衰退の一因であるとかなんとか。ふうん。
• 著者曰く、モチベーション・リサーチは80年代の消費文化理論(CCT)のご先祖様である由。はあ、そうですか。

論文：マーケティング - 読了： Tadajewski(2006) モチベーション・リサーチ、その勃興と衰退

2013年5月 4日 (土)

Seetharaman, P.B., (2004) The additive risk model for purchase timing. Marketing Science, 23(2), 234-242.
　購買間隔のモデリングにおける、Cox比例ハザードモデル(PHM)、加法リスクモデル(ARM), 加速故障時間モデル(AFTM)のパフォーマンスを比較します、という論文。
　著者いわく... 世帯の購買間隔のモデリングに際してもっともよく使われているのはPHMだ。ベースライン・ハザード関数としてよく用いられるのは、Erlang-2、ワイブル分布、対数ロジスティック分布、ゴンペルツ分布など。quadratic Box-Coxや Expo-powerが使われることもある (それぞれ Jain & Vilcassim 1991 Marketing Sci., Saha & Hilton 1997 Economic Letters をみよとのこと)。また離散時間PHMが用いられることもある (Helsen & Schmittlein 1993 Marketing Sci. をみよとのこと)。適用例は山ほどある。素晴らしい。しかあし、PHMにつきものの「マーケティング変数の影響が乗法的だ」という仮定は検証されていない。いっぽう、ARMを使った論文は、領域問わずに探しても90年以降たったの9本しかみあたらない。ひどいじゃないか。とのこと。

　ARMとAFTMってのはどういうのかというと... 前回購買からの経過時間を t , 共変量(価格とか) の行ベクトルを X_t として、世帯 i のハザード関数を
　　h_i (t, X_t) = h_i (t) + exp(X_t \beta)
とするのが ARM である(PHMではかけ算にするところを足し算にする)。以下、これを離散時間にして(grouped ARM)、ベースライン・ハザードは対数ロジスティック分布にして、s個のサポートで個人差を表現するモデルを使う。
　AFTMは、ハザードをベースライン・ハザードと共変量の効果にわけて考えず、ハザードそのものを共変量の関数にする。えーっと、対数ロジスティック関数はスケールをa, 形状をbとして
f(x) = [ (b/a)(x/a)^{b-1} ]/[ 1 + (x/a)^b]^2
だが (いまwikipediaで調べました)、本文中のハザード関数は、このxをt、bを\alpha, 1/aをX_tの線形関数 \gamma_0 + X_t \gamma_1 としたものになっているようだ。

　データはIRIのスキャナパネルデータ。洗濯洗剤、ペーパータオル、トイレットペーパーの購買にあてはめる。共変量は価格、ディスプレイ、チラシ。なんだか既視感があると思ったが、これきっとSeetharaman & Chintagunta (2003)と同じデータだ。あの論文を読んだときも悩んだのだが、購買は日次でわかっているんだけど、モデル推定時は週次データにして使っているんだと思う。
　推定の結果は... モデルの適合度やホールドアウトへの予測は、ARM, PHM, AFTMの順に良い。推定されたベースライン・ハザード関数の形状はだいたい同じで、だいたい10日目くらいまで急上昇、あとはなだらかに低下。共変量の係数をみると、PHMだけなんだかヘン(価格の係数が正になってしまうサポートがある)。サポートをつぶした価格弾力性の時系列曲線を求めると、ARMとAFTMでは解釈可能な曲線が得られたが、PHMではずっと 0 近辺になってしまった。ベースライン・ハザード関数を対数ロジスティックから他の形状に切り替えると(指数、Erlang-2、ワイブル、expo-powerを試している)、ARMではどの形状でも結果は大差がないが、PHMでは大きく変わってしまった。というわけで、ARMは優れています。とのこと。

　前回同様、とてもわかりやすい論文で、勉強になった。Marketing Scienceって、高級スーツを着たエリート様が偉そうな理屈で素人をたぶらかすというイメージがあるんだけど、こういうシンプルかつクリアな内容の論文も載るんですね。(←素朴すぎる感想だ)
　わかりやすかったおかげで、いろいろと疑問がわいた。第一に、ある統計モデルをデータにあてはめることの善し悪しの評価には、(1)データのあてはまりのよさや予測の良さ、(2)パラメータが安定していて筋が通っているか、そして(3)そのモデルそのものが背景知識と整合しているか、の３つの側面があると思う。この論文では、(1)の面ではARM, PHM, AFTMの順に良いということがわかり、(2)の面ではPHMがちょっとまずいということがわかった。でも、(3)の側面はいったいどうなっちゃったんだろう。「マーケティング変数が購買確率に加法的に効くかそれとも乗法的に効くか」という根本的な疑問に対しては、もっと心理的な観点からの議論、たとえば「購買時意思決定のほにゃららモデルに照らして考えれば、マーケティング変数はやっぱし加法的(or 乗法的)に効くと考えたほうが筋が通ってんじゃないですかねえ」というような議論があっても良さそなものだと思うのだけれど...
　第二に、「PHMがモデルのspecificationに対してセンシティブである」というのは、果たしてPHMの悪口になっているのかしらん。それはもちろん実務的にはですね、細かいオプションを多少変えても結果がロバストなモデルのほうが、非常に助かります。そのぶん早くうちに帰れるというものだ。でもそれは内輪話であって、いま池から神様が現れて、君が落としたモデルは正しく指定すれば正しい結果が得られるが間違って指定すると間違った結果が得られるモデルかい？ それとも指定に関わらずずーっとロバストに間違っちゃうモデルかい？ と聞かれたら、そのときはやっぱり、前者が欲しいと答えるべきだと思うわけである。ARMとPHMのどっちがいいかというのは、結局はシミュレーション研究でないとカタがつかない問題なのではないかという気がする。

論文：データ解析(-2014) - 読了：Seetharaman(2004) 購買データを分析するみなさん、比例ハザードモデルばっかり使ってないで加法リスクモデルをお使いなさい

2013年5月 3日 (金)

Manchanda, P., Dube, J.P., Goh, K.Y., & Chitagunta, P.K. (2006) The effect of banner advertising on internet purchasing. Jounral of Marketing Research, 43(1), 98-108.
　話題自体には関心がないのだが、Grover & Vriens (eds) の生存モデルの章で、時間変動共変量をいれた比例ハザードモデルのHB推定の例として挙げられていたので目を通した。第一著者は前に読んだ、複数カテゴリ購買についての(なんだか腑に落ちなかった)論文の第一著者で、少々腰が引けたが、背に腹は代えられない。いまは何でもいいから情報がほしいのだ。

　バナー広告がネット通販に及ぼす影響を、アクセスログと購買データで調べる。どうでもいいけど、結論を先にいえば、大事なのは露出であってクリックはどうでもよかった、効果には個人差があるのでちゃんとターゲティングしたほうがいい、トライアル購買に対する効果とリピート購買に対する効果は異なる、云々。

　あるネット通販専業会社のデータを使う。販売しているカテゴリはヘルスケア･化粧品・非処方薬。データはクッキー単位のアクセスログで、自社サイトへのアクセスと購買、自社サイトおよび他のサイトにおけるバナー広告の表示とクリックがわかる(出稿先の８割をカバーしている由)。これを週ごとの離散データにして分析する(週当たり購買は多くて1回となるよう前処理する)。書いてないけど、観察打ち切りのことは考えなくていいらしい。

　消費者 $i$ の $j$ 回目の購買について考える。前回の購買からの経過時間を $t_{ij}$ とする。時点 $t$ におけるハザード関数を $h(t)$ として、生存関数は
　$S(t_{ij}) = \exp( - \int_0^{t_ij} h(u) du )$
　これを離散化する。前回の購買からの観察期間を十分に長く取り、それを $J$ 個の区間に分割する。で、まず共変量のことは脇において、各区間におけるベースライン･ハザードの積分が定数だと考える(ピースワイズ指数ハザードモデル)。つまり、
　$\int_{(t-1)_{ij}}^{t_{ij}} h(u) du = \exp(\lambda_j) $
$(t-1)_{ij}$ というのがわかりにくいけど、これは「その区間の左端」という意味らしい。
　よし、次は共変量だ。比例ハザードモデルで考える。消費者 $i$ の $j$ 回目の購買までの間隔における $p$ 個目の共変量を $x_{pij}$ として、
　$\int_{(t-1)_{ij}}^{t_{ij}} h(u) du = \exp[ \lambda_j + \sum_{p=1} (x_{pij} \beta_{pi}) ]$
ベースラインを表す $\lambda_j$ は時点ごとに異なるが異質性はなく、共変量の係数 $\beta_{pi}$ は異質性があるが時間独立である。

　これを階層ベイズモデルに放り込む。
　$\Psi_j = log(\lambda_j)$ が $MVN(\Psi_0, V_\Psi)$ に従うと仮定する (なぜこういう風に仮定するのだろう？)。$\beta_{pi}$のベクトルが$\beta_i = \beta_0 + \nu_i$と分解され、$\nu_i$ は$N(0, V_\beta)$に従うと仮定する。$\beta_0$と$V_\beta$の事前分布はそれぞれMVN, 逆ウィシャート分布とする。$\Psi_0, V_\Psi$ もハイパーパラメータだと思うんだけど、事前分布は書いてない。

　以上のモデルを推定する。共変量として、バナー広告を見た回数の対数(LVIEWNUM)、その種類(ADNUM)、サイト数(SITENUM)、ユニークなページ数(PAGENUM)を使用。推定の結果、\Psi_j の分布の時系列変動は複雑で、ああピースワイズにしといてよかった、とのこと。共変量の係数はADNUMのみ負で、これはメッセージがバラバラだからじゃないか、とのこと。云々云々。
　推定結果についていろいろ分析していて、そこがこの論文の肝だと思うけど、いまんところ関心がないし、ほんとに頭が痛くなってきたのでスキップ。

　拝察するに、購買間隔に対する週単位の比例ハザードモデル、ベースラインハザードはノンパラメトリック、打ち切りなし、共変量はすべて時間依存、共変量の係数に消費者間異質性を想定。ということだと思うのだが... 正しいだろうか。
　想像するに、この通販業者にだってきっとロイヤル顧客とそうでない顧客がいて、共変量ではそれを説明できないくらいのばらつきがあるだろう(共変量は要するにすべてWebアクセスにすぎない)。だから、モデルのなかに「買いやすさ」というか、消費者間異質性があって時間独立な切片(frailty)を入れといたほうが気が利いているのではないか、と心配してしまったのだが... きっとなにか読み落としているのだろう。

論文：データ解析(-2014) - 読了：Manchanda, Dube, Goh, & Chitagunta (2006) ネット通販におけるバナー広告の効果を生存モデルで推定

Muthen, B. & Masyn, K. (2005) Discrete-time survival mixture analysis. Journal of Educatonal and Behavioral Statistics, 30(1), 27-58.
　離散時間生存モデルについての解説論文。とはいえ、なにしろ著者が著者だから、一般化された潜在変数モデル(mplusモデル)のなかで捉えて混合分布を使いましょうという話になる。長めの論文だけど、雑誌名に勇気づけられて読んだ。私の乏しい経験からいって、教育系の学術誌に載ったテクニカルな論文は、統計初心者むけに易しく説明してくれることが多い。(ついでにいえば、一番易しく書かれているのは臨床心理系だと思う。拝察するに、かの業界には「ふざけんな、もし数学が得意だったら医学部に行ってたよチクショウ」という人が多いからではないかしらん)
　離散時間生存モデルの長所として、著者らは以下の3点を挙げている:

1. 時間依存共変量を入れやすい。
2. 比例ハザード性の仮定がいらない。
3. "easily allow for unstructured as well as structured estimation of the hazard function at each discrete point." 読み進めてみると、unstructured/structuredというのは時点ごとのハザードになんらかの制約がかかっているかどうかという意味らしい。

　まず生存モデルについて。離散確率変数であるところの時間を T、時点 j におけるハザードを h_j とする。生存確率は S_j = \prod_{k=1}^j (1-h_k) 。ある人について考えると、

• 打ち切りに遭遇せず、イベントが時点 j において起きた場合、その尤度は P(T=j) = h_j S_{j-1}。
• 時点 j でドロップアウトした場合、その尤度は P(T>j-1) = S_{j-1}。
• 観察期間終了による打ち切りが起きた場合、最終観察時点の次の時点を j と呼べば、尤度は P(T>j-1) = S_{j-1}。

したがって、観察インジケータを \delta として、尤度は
　　l = h_j^\delta \prod_{k=1}^{j-1} (1-h_k)
標本全体の尤度は、全個人についての上の尤度の総積である。
　このハザードの推定について考えると、時間が離散的なので、各時点のハザードの標本推定値 (周辺ハザード) は単に、生きていた人における死んだ人の割合だ。簡単でよろしい。ハザードと共変量との関係を調べる際には、たとえばロジスティック・ハザード関数を使う。個人 i, 時点 j のハザードを h_{ij}、時間依存共変量ベクトルを z_{ij}、時間独立共変量ベクトルを x_i として、
　　h_{ij} = 1 / (1 + exp(-logit_{ij}))
　　logit_{ij} = \beta_j + \kappa'_{zj} z{ij} + \kappa'_{xj} x_i
このふたつの \kappaから添字 j を外して係数を時間独立にしたやつを、比例ハザードオッズモデルという由。ふうん。

　次に、mplusモデルのご紹介。共変量 x_i を持つ個人 i が属する潜在クラス c_i が k である確率を多項ロジスティックモデルで表して
　　P(c_i =K | x_i) \prop exp(\alpha_{c_k} + \gamma'_{c_k} x_i)
mplusでは最後のクラス K を基準クラスにするので、\alpha_{c_K} = 0, \gamma_{c_k} = 0 である。
　局所独立なクラス指標として二値変数ベクトル u_i を考え、その背後にある連続的潜在変数ベクトルを u^*_i 、閾値ベクトルを \tau とする。例によって、測定方程式は、切片を抜いて
　　u^*_i = \Lambda_k \eta_k + \Kappa_k x_i
構造方程式は、潜在変数間のパスを無視して
　　\eta_k =\alpha_k + \Gamma_k x_i
ああ、めんどくさい、詳細略。

　この枠組みに離散時間生存モデルをどうやって取り込むか。ひとことでいうと、時点の数だけ変数をつくり、多変量データにしてしまう。
時点 j においてイベントが起きたかどうかを二値変数 u_j で表す。ただし、もうイベントが起きちゃってるか、すでにドロップアウトが起きている場合は欠損にする(打ち切りが必ず欠損で表現されるという話ではない。最後の観察時点までイベントが起きなかったら、u_j はすべて 0 になる)。打ち切りが無情報である限り、このデータの欠損はMARである (ああ、なるほどね...)。したがって、ある人について考えると、

• 打ち切りに遭遇せず、イベントが時点 j において起きた場合、その尤度は P(T=j) = P(u_j=1) \prod_{k=1}^{j-1} P(u_k =0)。
• 時点 j でドロップアウトした場合、その尤度は P(T>j-1) = \prod_{k=1}^{j-1} P(u_k =0)。

したがって、観察インジケータを \delta として、尤度は
　　l = P(u_j=1)^delta \prod_{k=1}^{j-1} P(u_k =0)
最初に定式化したモデルと同じである。だから、h_j の最尤推定値は P(u_j=1) の最尤推定値と等しい。面倒なので省略するけど、さっき考えた h_{ij}と共変量のあいだのロジスティック・ハザードモデルも、mplusモデルでうまく表現できる。
　共変量がないとき、ハザードになんらかの制約をかけないかぎり、このモデルの自由度は0である。したがって潜在クラスを導入するには、ハザードに制約をかけるか、共変量を導入する必要がある。たとえば、観察期間終了による打ち切りの一部に「ハザードがどの時点でも0」であるような人がいると考える場合 (生存モデルではこういうのを長期生存者というそうだ)、それは「全時点で閾値が無限大、共変量の係数\kappaも潜在変数の係数\lambdaも0」という潜在クラスとして表現できるが、この潜在クラスを組み込んだモデルは共変量なしには識別できない(観察期間終了による打ち切りのうち誰が長期生存者なのかわからない、ということかしらん？)。

　事例は２つ。ひとつめは、刑務所から出てきてから再犯するまでのモデルで、共変量は出所後の財政的支援の有無(時間独立。実はこれ、制御変数である。すごい実験だなあ...)。まず比例ハザードオッズ性を確認する。仮に共変量の係数を時間依存だと考えると、u のひとつひとつに x から直接に矢印が刺さるモデルになる。いっぽう比例ハザードオッズ性を想定し、共変量の係数が時間独立だと考えれば、uのすべてにまず \eta から矢印が刺さり、xからは \etaに矢印が刺さるモデルになる(おおおお...)。後者のモデルの適合が良かったので、さらにハザードを個人内で一定にしたモデルと比較する。ええと、すべてのuの切片を等しく、かつ係数も等しくするんでしょうね。このモデルも適合が良い。これを採用した由。
　ふたつめは、入学してから退学するまでのモデル。共変量は攻撃的行動なのだけど、測定誤差を含んでいるので、そっちはそっちで潜在クラス成長モデルを組み同時推定する。潜在クラスも潜在変数も２つある。すいません、精力不足で付き合えません。

　うーむ。。。再犯の事例を読んでいて混乱してしまったが、発想をガラッと切り替えないといけないと気がついた。Muthenさんたちの枠組みで見た離散時間生存モデルは、パス図で書くとなんだか平凡なCFAやLCAのようにみえるが、要するにハザードの潜在成長モデルなのだ。潜在変数\etaは、因子というより成長曲線のパラメータだ(実際、推定結果の表の見出しにはツルッと"growth factor"と書いてある)。だから、潜在成長モデルについて考えるときに必要な、あの発想の転換を思い出さないといけない。そのことに気がついただけでも、目を通した価値があった。ということにしておこう。

論文：データ解析(-2014) - 読了：Muthen & Masyn (2005) 離散時間生存モデルへの招待

« 2013年4月 | メイン | 2013年6月 »