« 読了：Prelec, Seung, & McCoy (2017) 「みんなが思うよりも意外に多い」回答が正解だ | メイン | 「みんなが思うよりも意外に多い」回答はなぜ正しいか：その2 »
2017年8月17日 (木)
島根と鳥取、西側にあるのはどっちだろうか。あいにく地図が手元になく正解がわからない。そこで、たくさんの人に対してアンケートを行い、その回答の集計から正解を導きたい。
このとき、多数決はよろしくない。たとえば、西側にあるのはどっちだと思うかと人々に尋ねたところ、島根の得票率が4割、鳥取の得票率が6割となったとしよう。だからといって、鳥取が西側にある、と考えるのはよろしくない。
人々の知恵をうまく集約するには、むしろ次のように集計するのが良い。人々に2問尋ねる。(1)西側にあるのはどっちか。(2)自分と同じ回答をする人は何割いるか。で、「みんなが思うよりも意外に多い」回答が正解だと考える。
たとえば、(1)の回答で島根の得票率が4割であったとしよう。かつ、(2)の回答(得票率の予測)を平均すると島根が3割であったとしよう。つまり、「島根が西だ」という回答は全体の3割くらいだろうと人々は思ったが、実際には4割だったわけだ。このとき、「島根が西」説は少数派ではあるけれど、ほんとうは島根が西だと判断すべきだ。
... というのが、Prelec, Seung, & McCoy (2017, Nature)の主張である。
わたくし、ここ何年も、足りない頭でこの問題を考え続けているのだが、正直なところ、いまだにキツネにつままれたような思いが消えない。
なぜ「みんなが思うよりも意外に多い」回答が正解なのか？ 以下ではその徹底的な解説を試みる。
なお、元ネタは上記論文のSupplementary Information pp.1-8 である。４回にわけてゆっくり読み進めることにする。改めていうまでもないことだが、主たる想定読者は私自身である。
セッティング
いまここに$m$個の可能世界がある。うちひとつが現実である。私たちはどの世界が現実なのかを知らない。そこで、$m$個の選択肢を提示し、いずれが正しいと思うかを人々に聴取し、その回答から、どの可能世界が現実かを同定したい。
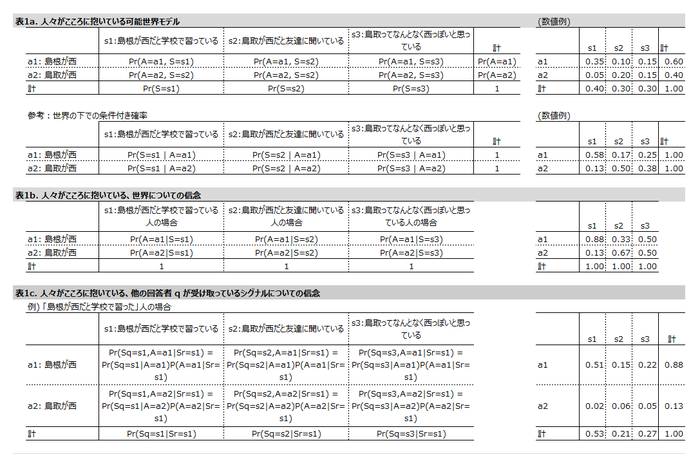
世界を確率変数$A$で表す[原文にはない記号だが、わかりやすくするために付け加えた]。$A$は$m$個の可能世界$\{a_1, \ldots, a_m\}$を値としてとる。[ここでは、$a_1$を「島根が西にある世界」, $a_2$を「鳥取が西にある世界」としよう]
対象者$r$が持っている証拠を、プライベートな「シグナル」$S^r$とみなす。対象者間の知識の差異はすべてシグナルで表現されていると考える。$S^r$はカテゴリカル確率変数で、値として$\{s_1, \ldots, s_n\}$をとる。[ここでは、$s_1$を「島根が西だと学校で教わった」, $s_2$を「鳥取が西だと友達に教わった」, $s_3$を「鳥取って西っぽいと思う」としよう。ある人の知識状態はこの3つのうちどれかひとつだ]
世界$a_i$の下で、異なる対象者のシグナルは独立に確率分布$Pr(S = s_k | A = a_i)$に従うと考える。[原文では$p(s_k | a_i)$と略記されているのだが、理解を確かめるために、以下いちいち確率変数名を補完して書き直す。縦棒左側の$s_k$は、ここでは$r$さんに限らずすべての人に与えられるシグナルを指しているのだと思うので、原文にそんな表記は出てこないけど$S$と書くことにする]
世界についての事前分布を$Pr(A=a_i)$とする。この事前分布は、すべての回答者の共通知識である証拠と整合的な確率を与えていると考える。[ここでの例でいうと、仮に知識ゼロの状態だったら、島根が西だと思うか鳥取が西だと思うかの信念の程度には個人差がない]
対象者は同時確率$Pr(S = s_k, A=a_i)$を知っていると想定する($Pr(A=a_i), Pr(S = s_k)$はともに0より大とする)。この同時確率が可能世界モデルを定義している。しかし人々は、どの$a_i$が正解($a_{i*}$)かを知らないし、シグナルの実際の分布も知らない。[すべての対象者は、こころのなかに表1aを持っている。この表自体には個人差はない。でも、人は自分が上の行の地球に生きているのか下の行の地球に生きているのかを知らない。また、この表のほかに、自分が何を知っているかは知っている。でも他の人がどんな知識を持っているかは知らない]
対象者は２つのタイプの信念を持つ。どちらの信念も、与えられたシグナル$s_k$と、既知の同時確率$Pr(S＝s_k, A=a_i)$から算出される。
- 正解についての信念$Pr(A = a_i | S = s_k)$。[表1b]
- 他の回答者が受け取っているシグナルについての信念 [表1c]。すなわち、ランダムに選ばれた他の回答者$q$について、
$Pr(S^q = s_j | S^r = s_k) = \sum_i Pr(S^q=s_j | A=a_i) Pr(A= a_i | S^r=s_k) $
[原文では右辺は$\sum_i p(s_j|a_i)p(a_i|s_k)p(a_i)$となっているのだが、最後に$p(a_i)$を掛ける理由がわからない... 大変僭越ながら誤植と捉えて取り除いている]
定理1
[私の理解では、ここは論文の本筋ではなく、前置きに当たる議論である]
定理1. 実際のシグナルの分布についての知識$Pr(S = s_k | A=a_i*)$と、それらのシグナルによって示唆される事後確率 $Pr(A=a_i | S = s_k)$に依存するアルゴリズムからは、正解は演繹できない。
証明：
以下では、これらのシグナル分布と、恣意的に選んだ答えについての事後確率を生成するような、ある可能世界モデルを構築することを試みる。
正解$a_{i*}$は未知、でもシグナルの分布 $Pr(S=s_k | A=a_{i*})$は既知だとしよう。また事後確率$Pr(A=a_j | S=s_k)$も既知だとしよう。[シグナルの分布を表2に示す。なお、本文で$a$の添え字が$i$じゃなくて$j$になっているのは、次の段落から$a_i$を「選択した任意の答え」という意味で用いるからではないかと思う]
任意の$a_i$を選び、それに対応する可能世界モデル$q(S=s_k, A=a_j)$を構築する。このモデルは、 $i*=i$であるときの既知のシグナル分布と事後確率を生成するものである。 [つまり、これから試したいことは、表1と表2から、表3を決めることだ。もし＜島根が西バージョン＞と＜鳥取が西バージョン＞の両方が作れたら、それは困ったことになる]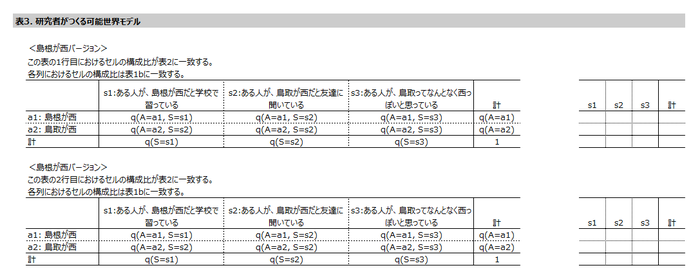 
既知のパラメータはシグナルを通じた事前分布を制約していない。そこで次のように設定しよう。
$\displaystyle q(S=s_k) = \frac{Pr(S=s_k | A=a_{i*})}{Pr(A=a_i | S=s_k)} \left( \sum_j \frac{Pr(S=s_j | A=a_{i*})}{Pr(A=a_i | S=s_j)} \right)^{-1}$
[第2項は$q(S=s_k)$の$k$を通じた和を1にするための規準化項。第1項の分子は表2。分母は、表1bにおけるいま選んでいる世界$a_i$の確率。なぜこう設定するのか理解できていないのだが、ここは「もし表3の列和をこう設定したら」という話がしたいだけで、意味を考えずに先に進んで良いところなのかも??? ともあれ、いま表3は下表のとおり]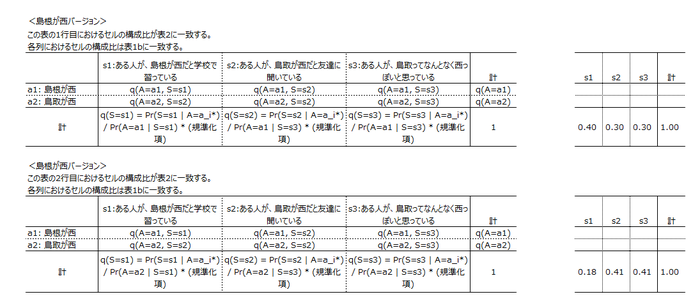
可能世界モデルから生成される事後確率は既知の事後確率と一致していないといけない。すなわち、全ての$k, j$について、
$q(A=a_j | S=s_k) = p(A=a_j | S=s_k)$
が成り立たなければならない。[表3の各列内のセル構成比が、表1bに一致していないといけない]
以上を踏まえると、可能世界モデルが次のように固定される。
$q(A=a_j, S=s_k) = q(A=a_j | S=s_k) q(S=s_k)$
この同時分布から、回答を通じた事前分布を求めることができる。まず
$q(A=a_i, S=s_k)$
$= q(A=a_i | S=s_k) q(S=s_k)$
さきほど設定した$q(S=s_k)$を代入すると、$q(A=a_i|S=s_k)=p(A=a_i|S=s_k)$が消えて
$\displaystyle = p(S=s_k | A=a_{i*}) \left( \sum_j \frac{p(S=s_j | A=a_{i*})}{p(A=a_i | S=s_j)} \right)^{-1}$
シグナルを通して合計すると
$\displaystyle q(A=a_i) = \left( \sum_j \frac{p(S=s_j | A=a_{i*}}{p(A=a_i | S=s_j)} \right)^{-1}$
こうして、可能世界モデルの周辺分布$q(S=s_k), q(A=a_i)$が手に入った。
さて、周辺分布$q(S=s_k), q(A=a_i)$、事後分布$q(a_j|s_k)=p(a_j|s_k), k=1, \ldots, n$からつぎのことがわかる。正解が$a_i$であるとき、観察されるシグナルの分布
$\displaystyle q(S=s_k | A=a_i) = \frac{q(A=a_i | S=s_k) q(S=s_k)}{q(A=a_i)}$
に、周辺分布$q(S=s_k), q(A=a_i)$を代入すると
$=p(S=s_k | A=a_{i*})$
となる。つまり、どんな$a_i$を選んでも、既知の事後分布を生成できる。証明終。
[このくだりの理路にはいまいちついていけないんだけど、こういうことじゃないかと思う。もし「島根が西」だといいたければ下表の上のような可能世界モデルを考えることができるし、「鳥取が西」だといいたければ下のような可能世界モデルを考えればよい。どちらも、表1と表2に対してつじつまが合う。いいかえると、表1と表2が決まっても、表3は決められない。]
[いまこの地球上において、 「島根が西だと学校で教わった」 「鳥取が西だと友達に教わった」 「鳥取って西っぽいと思う」 のそれぞれの知識を持つ人が占める割合$Pr(S = s_k | A=a_i*)$、すなわち表2が、どうやって調べるのかわかんないけど、とにかくなんらかのすごい方法でわかったとしよう。また、島根が西である時になにが起きるか、鳥取が西である時に何が起きるかについて人々は知っており(表1)、それもなんらかのすごい方法でわかったとしよう。研究者はこの2つの表を組み合わせて、島根が西なのか鳥取が西なのかを知ることができるだろうか？
一見できそうなものだが、実は無理なのだ、だから、たとえば回答とともにその確信度を聴取してみたりして、人々の知識をいくら正確に調べようとしたところで、世界がどうなっているのかは結局わからないんだよ。というのが、この定理がいわんとしていることなのだと思う]
これでようやくp.4の半ば。先は長いぞ。
雑記：データ解析 - 「みんなが思うよりも意外に多い」回答はなぜ正しいか：その1