« 覚え書き:差の集計としての共分散 | メイン | 読了:Wakimoto (1971) 層別抽出デザインにおける母分散・母共分散・母相関の推定 »
2018年7月29日 (日)
仕事の関連でお問い合わせ頂いて、いちおうお返事はしたんだけど、その途中で、よくよく考えてみたらこれって不思議だなあ、ということがでてきた。
層別抽出標本から母分散を推定するという問題について考える。標本推定量の分散の推定じゃなくて母分散そのものの推定である。こういう話、本にはなかなか載ってない。そりゃそうかもな、そんな用事はあんまりないような気もする。
層$h (=1,\ldots, H)$の$i(=1,\ldots,n_h)$個目の値を$x_{hi}$とし、層が母集団に占める割合を$P_h$とする。すべての層を通じた標本サイズを$n = \sum_h^H n_h$とする。
層ごとの平均は $\bar{x}_h = (1/n_h) \sum_{i}^{n_h} x_{hi}$
全体平均は $\bar{x}_{Total} = \sum_h^H P_h \bar{x}_h$
層ごとの分散は $S^2_h = (1/n_h) \sum{i}^{n_h} (x_{hi}-\bar{x}_h)^2$
層内分散は $S^2_{Within} = \sum_h^H P_h S^2_h$
層間分散は $S^2_{Between} = \sum_h^H P_h (\bar{x}_h - \bar{x}_{Total})^2$
全分散は層内分散と層間分散の和だから、$S^2_{Total} = S^2_{Within} + S^2_{Between}$が答えだ。と思いません??
例を挙げて計算してみよう。層1の値が$(1,2,3)$, 層2の値が$(1,2,3,4,5,6,7)$、どちらの層も母集団に占める割合は$1/2$とする。
層ごとの平均は$\bar{x}_1 = 2, \bar{x}_2 = 4$
全体平均は$\bar{x}_{Total} = 3$
層ごとの分散は $S^2_1 = 0.667, S^2_2 = 4$
層内分散は $S^2_{Within} = 2.333$
層間分散は $S^2_{Between} = 1$
全分散は $S^2_{Total} = S^2_{Within} + S^2_{Between} = 3.333$
となる。なりますよね?
とここまで考えて、あれれ?おかしいな?と気が付いた次第である。
だって、母分散を推定したいわけでしょ? 不偏推定したいでしょ? だったら、層ごとの分散の分母は$n_h$じゃなくて$n_h-1$じゃない?つまり、層ごとの分散は
$U^2_h = (1/(n_h-1)) \sum_i^{n_h} (x_{hi}-\bar{x}_h)^2$
じゃない?
こうして求める全分散を$U^2_{Total,1}$と呼ぼう。実例で計算し直すと
層ごとの分散は $U^2_1 = 1, U^2_2 = 4.667$
層内分散は $U^2_{Within} = 2.833$
全分散は $U^{2}_{Total,1} = U^2_{Within} + S^2_{Between} = 3.833$
となる。
とここまで考えて、さらに、あれれ?さらにおかしいな?と気がついたわけである。
層ごとの分散$S^2_h$を標本分散から不偏分散に代えたのに、層間の分散$S^2_{Between}$はそのままでよろしいわけ?
散々探してついに見つけたのだが、よろしくないらしい。Wakimoto(1971)によれば、母分散の不偏推定量は
$U^2_{Total} = U^2_{Within} + S^2_{Between} - \sum_h^H P_h(1-P_h) U^2_h/n_h$
なのだそうである(p.235, 記号は原文から書き換えました)。$S^2_{Between}$はちょっと大きめになってしまうので第3項を引く、っていうことなんじゃないかと思う。
これを$U^2_{Total,2}$と呼ぼう。実例で計算し直すと、
層間分散は $U^2_{Between} = 1 - 0.25 = 0.75$
全分散は $U^2_{Total,2} = U^2_{Within} + U^2_{Between} = 3.583$
となる。
ところで... 四の五の言わずに、上記の$S^2_{Total}$を$n/(n-1)$倍すればいい、という考え方もあるかもしれない。
この考え方は次のように言い換えることもできる。母分散ってのは値と母平均との差の二乗の母平均のことであり、不偏分散ってのは値と標本平均の差の二乗の合計を(標本サイズ-1)で割った値のことだ。だから、まず全体平均$\bar{x}_{Total}$を求め(もちろん単純な平均ではなく、層ごとの平均を$P_h$で重みづけて合計する)、次に標本のそれぞれの値から$z_{hi} = (x_{hi} - \bar{x}_{Total})^2$を求め、その合計を求め(各層の合計を$P_h$で重みづけて合計する)、最後に$n-1$で割ればよい。
あるいは、こういう風に考えることもできる。複雑な抽出デザインのデータを分析する際によく行われているように、それぞれの値に確率ウェイトを付与しよう。層別抽出の場合、確率ウェイトとは、各層における標本抽出確率(母集団のある層に属しているある個体が、標本として選ばれる確率)の逆数に比例した値である。このデータの場合、層1では5/3=1.667, 層2では5/7=0.714を与えればよい。さて、このデータが層別抽出であることを無視し、データ$x_1, \ldots, x_n$にウェイト$w_1, \ldots, w_n$が付与されているのだと考える。このウェイトを頻度ウェイト、すなわち「標本におけるその行の出現頻度」として捉えてしまい、不偏分散
$\sum_i^n w_i (x_i - \bar{x}_{Total})^2 / (\sum_i^n w_i - 1)$
をしれっと求める。
これを$U^2_{Total, 3}$と呼ぼう。実例で計算すると、
全分散は $U^2_{Total, 3} = S^2_{Total} * n / (n-1) = 3.333 * 10 / 9 = 3.704$
では統計ソフトでやってみよう。Mplus, SAS, Rで試す。
Mplusの場合、次のようなコードで試してみたところ
DATA:
FILE IS data.dat;
VARIABLE:
NAMES ARE X nStrata gWeight;
WEIGHT = gWeight;
STRATIFICATION = nStrata;
ANALYSIS:
TYPE = COMPLEX; 分散は3.333と推定された。すなわち$S^2_{Total}$である。
これはまあ、わかる。標本分散は母分散の不偏推定量ではないが、正規分布に従う変数については、母分散の最尤推定量である。MplusはXの正規性を仮定し、最尤推定値を返しているわけだ。これはMplusのポリシーなので、そうですか、としかいいようがない。
SASの場合、層別抽出で得た平均の分散を求めることは簡単なんだけど(PROC SURVEYMEANS)、母分散はすぐには推定できそうにない。散々探した末、ようやくSAS社による解説を発見した。
サンプルコードを書き換えたコードがこちら。SAS University Editionで試しました。
dm log 'log; clear' ; dm output 'output; clear';
data ttt;
input strata value;
datalines;
1 1
1 2
1 3
2 1
2 2
2 3
2 4
2 5
2 6
2 7
;
run;
data ttt;
set ttt;
if strata = 1 then weight = 5/3;
if strata = 2 then weight = 5/7;
run;
proc surveymeans data = ttt mean stacking ;
stratum strata ;
var value;
weight weight;
ods output Statistics = Statistics Summary = Summary;
run;
data _null_;
set Statistics;
call symput("Mean", Value_Mean);
run;
data Summary;
set Summary;
if Label1="重みの合計" then call symput("N",cValue1);
run;
%put _user_;
data Working;
set ttt;
z=(1/(&N-1))*(value-&Mean)**2;
run;
proc surveymeans data = Working sum stacking;
weight weight;
var z;
run;
結果は3.704、つまり$U^2_{Total, 3}$である。あっれえええ?
コードを読むとわかるのだが、ここでやっているのは、「$z_{hi} = (x_{hi} - \bar{x}_{Total})^2$の合計を$n-1$で割る」という、まさに$U^2_{Total, 3}$の考え方に従った処理なのである。
Rの場合、複雑な抽出デザインの分析はsurveyパッケージが定番である。母分散を推定する関数はsvrvar()である。次のコードで試してみたところ
dfData <- data.frame(
X = c(1,2,3,1,2,3,4,5,6,7),
nStrata = c(rep(1, 3), rep(2, 7)),
gWeight = c(rep(5/3, 3), rep(5/7, 7))
)
oDesign <- svydesign(
ids = ~ 0,
strata = ~nStrata,
weight = ~gWeight,
data = dfData
)
print(svyvar(~ X , data=dfData, design=oDesign, estimate.only =TRUE)) 分散は3.704と推定された。あっれえええ?
svyvar()のコードをちょっと眺めてみたんだけど、やはり$U^2_{Total, 3}$のような処理をやっている模様である。
というわけで、SAS社のお勧めの方法でも、Rのsurvey::svyvar()でも、母分散の推定量は$U^2_{Total, 3}$となっていることがわかった。
私、正直、納得いかないです... 正しい推定量は$U^2_{Total, 2} $なのではなかろうか?
毒を喰らわば皿まで、ということで、シミュレーションしてみた。
層は2つとする。変数$X$は、層1においては$N(0,1)$に、層2においては$N(2,1)$に従うとする。層内分散は$1$、層間分散は$1$、よって母分散は$2$である。
ここからサイズ100の標本を層別抽出し、母分散を推定する。標本における層1のサイズは(10,20,30,40,50)の5水準とし、各水準につき50000回繰り返した。
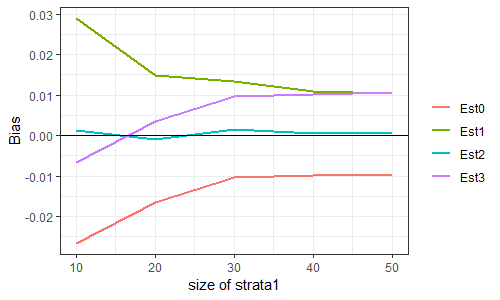
50000個の母分散推定値の平均から2を引いた値をBiasと呼ぶことにする。これが0に近い推定量が、(不偏性という意味で)良い推定量である。
推定量は、上記の$S^2_{Total}, U^2_{Total,1}, U^2_{Total,2}, U^2_{Total,3}$の4種類。順にEst0, Est1, Est2, Est3と呼ぶことにする。SAS社の解説やRのsurveyパッケージの出力はEst3である。私が申し上げたいのは、Est2を出力してくれたらいいのになあ、Est3にはバイアスがあるのになあ、ということであります。
コードと結果はこちら。
library(MASS)
library(dplyr)
library(tidyr)
library(ggplot2)
# - - - - - -
nTOTALSIZE <- 100
anSIZE1 <- seq(10,50,10)
nNUMITER <- 50000
agMU <- c(0, 2)
agSIGMASQ <- c(1, 1)
agPROP <- c(1/2, 1/2)
# - - - - - -
set.seed(123)
sub_EstimateVar <- function(dfIn){
anSize <- tapply(dfIn$X, dfIn$nStrata, length)
agMean <- tapply(dfIn$X, dfIn$nStrata, mean)
agUnbiasedVar <- tapply(dfIn$X, dfIn$nStrata, var)
agSampleVar <- agUnbiasedVar * (anSize - 1) / anSize
agProp <- tapply(dfIn$gWeight, dfIn$nStrata, sum) / sum(dfIn$gWeight)
gTotalMean <- sum(agProp * agMean)
agBetweenVar <- sum(agProp * (agMean - gTotalMean)^2)
gEst0 <- sum(agProp * agSampleVar) +agBetweenVar
gEst1 <- sum(agProp * agUnbiasedVar) +agBetweenVar
gEst2 <- sum(agProp * agUnbiasedVar) + agBetweenVar - sum(agProp * (1-agProp) * agUnbiasedVar / anSize)
gEst3 <- gEst0 * sum(anSize) / (sum(anSize) -1)
out <- data.frame(
gEst0 = gEst0,
gEst1 = gEst1,
gEst2 = gEst2,
gEst3 = gEst3
)
}
# dfData <- data.frame(
# X = c(1,2,3,1,2,3,4,5,6,7),
# nStrata = c(rep(1, 3), rep(2, 7)),
# gWeight = c(rep(5/3, 3), rep(5/7, 7))
# )
# print(sub_EstimateVar(dfData))
lOut <- lapply(
anSIZE1,
function(nSize1){
lOut <- lapply(
1:nNUMITER,
function(nIter){
nSize2 = nTOTALSIZE - nSize1
data.frame(
nSize1 = nSize1,
nIter = nIter,
X = c(
rnorm(nSize1, agMU[1], agSIGMASQ[1]),
rnorm(nSize2, agMU[2], agSIGMASQ[2])
),
nStrata = c(rep(1, nSize1), rep(2, nSize2)),
gWeight = c(
rep(agPROP[1]/(nSize1/nTOTALSIZE), nSize1),
rep(agPROP[2]/(nSize2/nTOTALSIZE), nSize2)
)
)
}
)
bind_rows(lOut)
}
)
dfIn <- bind_rows(lOut)
out <- dfIn %>%
group_by(nSize1, nIter) %>%
dplyr::do(sub_EstimateVar(.)) %>%
ungroup() %>%
group_by(nSize1) %>%
summarize(
Bias_Est0 = mean(gEst0) - 2,
Bias_Est1 = mean(gEst1) - 2,
Bias_Est2 = mean(gEst2) - 2,
Bias_Est3 = mean(gEst3) - 2,
RMSE_Est0 = sqrt(mean((gEst0 - 2)^2)),
RMSE_Est1 = sqrt(mean((gEst1 - 2)^2)),
RMSE_Est2 = sqrt(mean((gEst2 - 2)^2)),
RMSE_Est3 = sqrt(mean((gEst3 - 2)^2))
) %>%
ungroup()
dfPlot <- out %>%
gather(sVar, gValue, -nSize1) %>%
separate(sVar, c("sVar1", "sVar2")) %>%
filter(sVar1 == "Bias")
g <- ggplot(data=dfPlot, aes(x = nSize1, y = gValue, group=sVar2, color=sVar2))
g <- g + geom_path(size=1)
# g <- g + facet_grid(. ~ sVar1)
g <- g + geom_abline(slope=0, intercept=0)
g <- g + labs(x = "size of strata1", y = "Bias")
g <- g + scale_color_discrete(name = "")
g <- g + theme_bw()
print(g)
...ほらね?
2018/07/31: SASのコード、Rによるシミュレーションをつけ加えました。
雑記:データ解析 - 覚え書き:層別抽出標本から母分散を推定する方法(シミュレーションつき)