2020年3月22日 (日)
Tポイントとかdポイントとか、ああいうロイヤリティ・プログラムの「ポイント」についての資料。仕事の関係で目を通した。論文じゃないけど、読んだものは何でも記録しておこう、ということで...
翁百合(2019) ポイント経済化について -マクロ経済や金融システムへのインプリケーションを探る-. 日本総研リサーチレポート, 2019-010.
概観:
- NRIによれば2018年度のポイント発行額は9546億円。これは企業の売上とかにポイント適用率と還元率をかけて推計している。いっぽう金融庁は引当金(負債に属する)の合計額の推移を調べている。
- クレカ・家電量販・携帯電話で発行額が多い。伸びているのはプラットフォーマー企業のポイント。
- ポイントの利用率(失効率)はよくわからない。
- ポイント交換のネットワークは複雑化している。必ずしも交換が進んでいるわけではない。交換自体をビジネス化する動きもある(ネットマイルとか)。
- プラットフォーマーはキャッシュレス決済の経済圏をつくりポイント付加で囲い込みを図っている。
- ポイントを投資に転換する動きもある。これについては金融庁が前向きな方針を示している [←へー]
ミクロにみると、個社発行ポイント(プラットフォーマーでない企業のポイント)とは、企業が消費者の価格弾力性に注目し、将来の値引き分の決済手段をトークンとして渡すもの。いっぽうプラットフォーマーは、還元額の多くを加盟店に負担させる形でトークンを付与する、というちがいがある。
プラットフォーマーがポイント還元を積極的に活用するとなにがおきるか? 3つにわけてみていく。
A. 消費の質の変化。先行研究ではふたつの視点がある。
A1. ポイントがスイッチングコストとして作用し、ロックインが起きる。この観点からいえばポイント交換はスイッチングコストを下げる。
A2. 行動経済学的視点でいうと、ポイント付与の表現を工夫したり参照点を変えたりしてフレーミング効果を起こす。[このくだりは先行研究列挙に近い。寺地・近(2011行動経済学), 泉谷(2013放送大の紀要), 中川(2015行動経済学), 山本(2011立教の紀要), Liu(2007 J.Mktg)]
というわけで、ポイントはロックインにより消費者余剰を低下させている可能性がある。また、キャッシュレス化、データ活用による個別消費提案、消費者行動の非合理化(ポイントを貯めるための貯めるための追加消費とか)が起こりうる。
B. 価格のカスタム化。先行研究ではポイントを非線形プライシングととらえる見方がある。また、企業は景気が悪くなると囲い込んだ顧客に高めの価格をつける傾向があるので、counter cyclicalな効果があるかもといわれている。
というわけで、物価指数が実態から離れるかも。なお、プラットフォーマー型ポイントは価格決定力が加盟店にないからcounter cyclicalな効果は小さかろう。
C. ポイントの疑似貨幣化。先行研究では...[中略]。ただし、仮に年5000億のポイントが決済に使われているとしても、電子マネーの決済金額は約5.5兆、それほど大きくない。また、1単位当たりの価値がばらばらだし交換が限定されているし期限があるし還流しない。貨幣の3機能(価値尺度、流通手段、価値貯蔵)をすべて満たさない。今後のプラットフォーマー型ポイントの進展によってはわかんないけど。
むしろポイントを貯めること自体に楽しみを見出す人も多いわけで、法定通貨にない魅力があるのかもしれない。貨幣の多様性の展望を拓くものともいえる。
云々。
... いっちゃなんだけど、もう少し体裁に気を配ればいいのに、と思った。ちゃんと校正するとか、数式を数式フォントで書くとか。こういうのを読む専門家の方は、そのへんあんまし気にしないのかなあ...
ポイントについての研究を探すとみつかるのはたいてい購買をアウトカムにとった行動経済学的な話なんだけど(ポイント付与と値引きがどう違うかとか)、そうじゃなくて、ポイント獲得行動そのものといえばいいのか、ケインズのいう貨幣愛ならぬポイント愛といえばいいのか、この資料でいうとCの最後の論点に関心があって、理論面での先行研究を探しているんだけど、見当たらない。このレポートでもアンケートを紹介しているだけだった。ううむ。
論文:マーケティング - 読了:翁(2019) マクロ経済に対する「ポイント」の影響
2020年3月19日 (木)
コロナ騒動で気が休まらない毎日でありますが、感染者数の推移や予測がメディアにさかんに取り上げられていて、ああ、こういう研究ができたら面白かったろうな... などと無責任なことをぼんやり考えていた次第である。
で、フォルダを整理していたら、「いずれ読む」PDFのフォルダにそっち方面の概説論文がはいっているのをみつけた。全然覚えていないんだけど、仕事の参考になるかと思って深く考えずに保存していたのだと思う。
せっかくなので、仕事の待ち時間にめくってみた。
西浦博, 稲葉寿 (2006) 感染症流行の予測:感染症数理モデルにおける定量的課題. 統計数理, 54(2), 461-480.
まずはSIRモデルから。
感染する可能性のある人を$S$, 感染している人を$I$, 免疫を獲得したか死んだ人を$R$として、
$\frac{dS(t)}{dt} = -\beta S(t) I(t)$
$\frac{dI(t)}{dt} = \beta S(t) I(t) - \gamma I(t)$
$\frac{dR(t)}{dt} = \gamma I(t)$
$\beta$は感染率。$\beta I(t)$を感染力という。$\gamma$は回復率や隔離率で、$\gamma^{-1}$を感染期間が指数分布に従うと仮定した平均値とする。短期的な流行のモデルなので人口動態は無視する。
総人口を1として、平衡状態$(S(t), I(t), R(t)) = (1,0,0)$において
$\frac{dI(t)}{dt} = (\beta - \gamma) I(t)$
が成り立つ。感染初期に感染者は$I(t) \approx I(0) \exp{(\beta -\gamma)t}$と指数関数的に増えるわけだ。病気が集団に侵入可能になるのは$\beta - \gamma > 0$のときである。ここから
$R_0 = \frac{\beta}{\gamma}$
を基本再生産数という。R noughtと発音する。[←完璧な門外漢なので、このくだりを読んだだけでもう元をとったという感じだ。SIRモデルについては読んだことがあったけど、いまメディアでみかける基本再生産数って全然意味がわかってなかった]
時刻 $t$までに感染を経験した人を $N(t) = S(0) - S(t)$とすると... [残念ながらこの段落は知識不足で理解できなかったので、メモも省略。シグマ代数ってなに?]
SIRモデルの拡張。
$I$をさらに、曝露したけどまだ感染性を持たない状態$E$と感染性を持つ状態$I$にわけると
$\frac{dS(t)}{dt} = -\beta S(t) I(t)$
$\frac{dE(t)}{dt} = \beta S(t) I(t) - \epsilon E(t)$
$\frac{dI(t)}{dt} = \epsilon E(t) - \gamma I(t)$
$\frac{dR(t)}{dt} = \gamma I(t)$
$\epsilon$は「曝露後に感染性を得る率」。これをSEIRモデルという。
ほかにもモデルが作れる。免疫が獲得できないSIRSモデルとか。
基本再生産数の意義として、予防接種率の達成目標について考えると...
効果$\epsilon$のワクチンを接種率$p$で実施したとき、免疫を持たない人の割合は$1-\epsilon p $だから、接触パターンがhomogeneousなら再生産数は$(1-\epsilon p) R_0$。これを1未満にすれば感染症は終息する。$p$について解くと $p > 1 / \epsilon (1-1/R_0)$だ。[←うぉー おもしれええ]
$R_0$の推定は、さすがに決定論的に考えてると精度とかを考慮できないので、確率論的なモデルを考えて...[めんどくさいからメモは省略するけど、そんなにものすごく難しい話ではなさそう。ふつうはML推定量が閉形式で書き下ろせるらしい。$\beta$の時間変動とか感受性の異質性とかを考慮したモデルをMCMC推定したりするのもあるのだそうだ。ふへえええええ]
実際には伝播能力は行動の変化とか公衆衛生施策とかで時間変動するので、そういうのを考慮したのを効果的再生産数($R_t$)という。実際の感染ネットワークから求めたり、理論的に求めたりできる。SARSの流行時にWHOが緊急事態のアラートを出した直後に$R_t$が1未満になったという研究があるそうだ[←へえええええ!]
感染待ち時間・感染性期間の分布を天下りに与えるのではなく、観察に基づき適切な分布を推定するというアプローチもある。
感染待ち時間は潜伏期間と似ているので(潜伏期間の途中から感染性があることが多いから、ほんとはちょっとちがうんだけど)、調査で調べた潜伏期間の分布で代用したりする(対数正規分布に従うことが多い)。検疫に必要な目安の時間がわかったりする。[途中から難しくなってきたので大幅中略]
いっぽう感染性期間の分布を知るのは難しい。感染待ち期間と潜伏期間は似ていることが多いけど、感染性期間と症候性期間はちがう。たとえばHIVの場合、感染した直後にウィルスが多く、いったん下がってAIDS発症の前にまた上がる。[...] 実際のウィルス量と疫学的な感染性との評価指標との相関はまだ確実でなく、今後の課題である。[←へえー。個人レベルの機序と集団レベルの現象の関係が意外にはっきりしないってことなのね... ウィルス量の増減も人によっていろいろってことかしらん]
接触性の異質性を考慮するという方向の拡張もある。[...中略するけど、ひとつのアプローチはそのなかでは接触パターンが均一であるような複数のsubpopulationを考えるという方法で、これをmultitype epidemicモデルというのだそうだ。よくわかんないけど潜在クラスモデルみたいになるのだろうか...]
最近関心が集まっているのは、接触関数の頻度分布がべき乗分布に従うとき(スケールフリーなとき)で、感染症の制圧は困難を極める。
接触頻度に関する定量的説明は性感染症から明らかになるだろうと期待されている。接触回数の計数が観察可能だから。[←これ、誰と何回セックスしたかインタビューで正直に答えるだろうから、って意味だろうか...?]
あれこれ考えているとどんどん複雑になるので、観察データじゃなくて介入研究でパラメータ推定することも多い。[←うぉー面白い!と思ったんだけど、どういう実験になるのか想像がつかなかった...]
云々、云々。
...半分くらいはちんぷんかんぷんだったんだけど、仕事と直接関係しないという気楽さもあって、いやー、面白かった。もっと頭がよくて若かったら、こういうのやりたかったなあ... (← 一時の気の迷い)
ともあれ、研究者の方々のご奮闘をお祈りいたします。
論文:データ解析(2018-) - 読了:西浦・稲葉(2006) 感染症流行の予測
2020年3月11日 (水)
仕事の都合であれこれ考えていたらわけがわからなくなってしまったので、ちょっとシミュレーションをやってみたら、さらに新たな疑問が生じ... という話を記録しておく。
背景
ある量的変数の時系列 $Y_t$ があって、それに影響を及ぼしているであろうなんらかの変数の時系列$X_t$があるとする。なんでもいいんだけど、たとえば売上と広告出稿量とか。
で、$Y_t$に対する$X_t$の効果の大きさをデータから推定したい。こういうこと、よくありますよね。
話を簡単にするために、分析者は次のことを知っているとしよう。
- $X_t$の$Y_t$に対する効果は即時的、かつ線形である。つまり、
$Y_t = \alpha + \beta X_t + V_t$
とモデル化できる。 - $X_t$は定常である。なんでそんなことを知っているのかわからんが、なにか実質的な知識があるのでしょう。
- $Y_t$の撹乱項$V_t$は一次自己回帰過程 (AR(1)過程)に従う。つまり、
$V_t = \rho V_{t-1} + E_t, \ \ E_t \sim N(0, \sigma_E^2)$
とモデル化できる。これも、まあ、ありそうな仮定ですわね。時系列の自己相関関数を観察した結果、これAR(1)でいいんじゃね? と思うことはさほど珍しくないと思う。 - 自己回帰係数$\rho$は$0 \leq \rho \leq 1$である。つまり、$V_t$は非負の自己回帰係数を持つ定常AR(1)過程に従う($0 \leq \rho <1$)か、単位根AR(1)過程に従う($\rho = 1$)かのどちらかである。これもそれほど変な仮定ではないと思う。自己回帰はふつう正だし、もし負だったらデータの観察でそれと気がつくだろう。仮に$\rho >1$なら$V_t$はどっかに飛んでいってしまうはずなので、これも除外できる。でも、$\rho <1$か$\rho = 1$かは簡単には判断できない。
問題
さて、分析者が関心を持っているのは$\beta$である。ここで疑問なのは、$\beta$の推定誤差は$\rho$とどういう風に関連しているのか、という点である。特に次の点について知りたい。
- Q1. $\rho$が大きいとき、つまり結果変数の撹乱項が高い自己相関を持つとき、$\beta$の推定誤差は大きくなるか、それとも小さくなるか。
- Q2. $\rho = 1$であるのにそれと知らず、$\rho < 1$と仮定するモデルを推定したとき、$\beta$の推定誤差は大きくなるか。
いずれも、私にとってはちょっと切実な疑問だ。
Q1についていえば... 仕事のなかで時系列データの分析が生じる際、まずは目的変数の時系列を観察して、これからわざわざ説明変数のデータを集めモデリングする労力は報われるかしらん? と算段することが多いと思う。そういう場面での手掛かりがほしい。見通しが暗いなら早めに白旗を上げたい。
Q2についていえば... 理屈の上からいえば、$\rho=1$かそうでないかでAR(1)過程の挙動はがらっとかわる。でも、実データの背後にあるデータ生成プロセスが$\rho=1$かどうかなんて、どうせわかりっこない。だから、きっと$\rho<1$だよねと信じてAR(1)誤差を仮定したり、いや$\rho=1$にちがいないと信じて差分時系列を分析したりするわけである(そんなことないですか?)。でも心には常に不安の影が付きまとう。$\rho$についての仮定をしくじることが、$\beta$の推定にとってどのくらい致命的なのかを知りたい。
方法
気になって夜も眠れないので(大げさな表現)、簡単なシミュレーションをやってみました。
$t=-100,\ldots,100$について、データを次のように生成した。
$x'_t \sim unif(0, 1)$
$e_t \sim N(0, 1)$
$v_t = \rho v_{t-1} + e_t$
$y'_t = x't + v_t$
つまり$\beta = 1$である。で、$x'_t, y'_t$から$t=1$以降を切り出し、それぞれを中心化する。これを$x_t, y_t$とする。
$\rho$を$0, 0.1, 0.2, \ldots, 1.0$の11通りに動かし、それぞれについて1000個のデータセットを生成した。
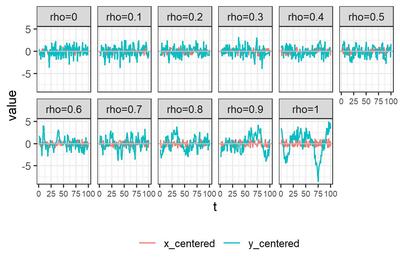
それぞれについてデータセットをひとつ選び$x_t, y_t$を描画すると、こんな感じである。
モデルの推定方法として、次の6つを試す。
- A. 単にOLS推定
- B. Rのforecast::Arima()でML推定
- C. Rのnlme::gls()でFGLS推定
- D. 状態空間モデルとして定式化し、RのKFASパッケージを使ってカルマンフィルタで推定
- E. Mplusでベイズ推定
- F. Stanでベイズ推定
推定にあたっては、次の5つのアプローチを試してみる。
- アプローチ1. $\rho = 0$と仮定して、
$y_t = \beta x_t + e_t$
$e_t \sim N(0, \sigma_e^2)$ - アプローチ2. $|\rho| < 1$と仮定して、
$y_t = \beta x_t + v_t$
$v_t = \rho v_{t-1} + e_t, \ \ |\rho| < 1$
$e_t \sim N(0, \sigma_e^2)$ - アプローチ3. $\rho = 1$と仮定し、$\Delta y_t = y_t - y_{t-1}, \Delta x_t = x_t - x_{t-1}$について、
$\Delta y_t = \beta \Delta x_t + e_t$
$e_t \sim N(0, \sigma_e^2)$ - アプローチ4. $y_t$について単位根検定を行い、単位根を持たないと判断されたらアプローチ2, 持つと判断されたらアプローチ3に進む。
- アプローチ5: アプローチ2と同じなんだけど、$\rho$の範囲について仮定しない。
私の乏しい理解では、A(OLS), B(ML), C(FGLS)では撹乱項の定常性が仮定されるので、アプローチ5は選べない。いっぽうD(カルマンフィルタ), E,F(ベイズ)では、$\rho$を明示的に制約しないかぎりアプローチ5になる... というように理解しているのだけれど、ここ、全然自信がない。悲しい。誰か私に教えてくださらないでしょうか。
まあいいや!とにかくシミュレーションしてみたのであります。
単位根検定
まず、アプローチ4で必要になる単位根検定の結果について紹介しておく。Dickey-Fuller検定を使った。Rコードはこんな感じ。$y_t$がdfIn$y_centeredにはいっている。
library(urca)
oDFTest <- ur.df(dfIn$y_centered, type = "none", lags = 1)
nD <- if_else(oDFTest@teststat[1,1] < oDFTest@cval[2], 0, 1)
トレンドもドリフトもないAR(1)であると知っているので、type ="none", lags=1と決め打ちしている。$H_0: \rho=1$が 5%水準で棄却されたら$\rho<1$と判断し、そうでなかったら$\rho=1$と判断することにして、後者の場合にnDを1としている。
素朴に考えると、本当は$\rho=1$であるデータセットのうち95%くらいが$\rho=1$と判断されてほしい($H_0$が真のときに誤って棄却される確率は5%であってほしい)。本当は$\rho<1$である場合は、なるべく多くのデータセットが$\rho<1$と判断されてほしい。
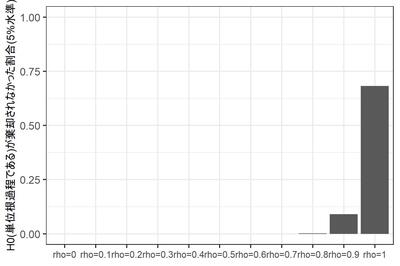
さて、11通りの$\rho$の、それぞれ1000個のデータセットのうち、$\rho = 1$と判断されたデータセットの数は?
蓋をあけてみると... $\rho=1$であるデータセットのうち、$H_0$が棄却されなかった($|\rho|=1$と判断された)データセットは95%には到底及ばず、実に68%にとどまる。なぜだろう? よくわからない。
$\rho<1$であるにもかかわらず$H_0$が棄却されないデータセットは、当然ながら$\rho$が1に近づくにつれて増えるのだが、それでも$\rho = 0.9$のときに9%。$\rho = 0.8$までではほとんど生じない。
このように、DF検定の場合、保守側($H_0: \rho = 1$が棄却されない側)に大きくバイアスがかかるようだ。$H_0$を反対側に設定するPP検定であればまた違う結果になるだろうけど...
まあとにかく、ここで確認しておきたいのは、$\rho = 1$かそうでないかなんて、そんなに簡単にはわからないよね、ということである。
選手紹介
お待たせしました、選手入場です。拍手でお迎え下さい。
A. 単にOLS推定。アプローチ1($\rho=0$と仮定)のRコードは
oModel <- lm(y_centered ~ 0 + x_centered, data = dfIn)
自己相関を華麗にスルーしちゃうわけだが、これ、それほど捨てたもんじゃないと思う次第である。だって、$|\rho| < 1$であれば、$\hat{\beta}$は少なくとも一致推定量ではあるわけでしょう?
アプローチ1, 3($\rho=1$と仮定)を試してみる。
B. forecast::Arima()で最尤推定。Rによる時系列モデリングの定番 forecast パッケージはArima()という関数をご用意している(実はstat::arima()へのラッパーである)。アプローチ2($|\rho|<1$と仮定)のRコードはこんな感じ。
library(forecast)
oModel <- Arima(
y = dfIn$y_centered,
include.mean = FALSE,
order = c(1, 0, 0),
xreg = dfIn$x_centered ,
method = "ML"
)
アプローチ3($\rho=1$と仮定)ならorder = c(0,1,0)となる。アプローチ2, 3, 4(DF検定で切り替え)を試す。
C. nlme::gls()でFGLS推定 ついでにnlme::gls()でFGLS推定を試してみる。計量経済学の教科書に載っているのは、最尤推定じゃなくてこっちのほうですね。
アプローチ2($|\rho|<1$と仮定)のRコードはこんな感じ。
library(nlme)
oModel <- gls(
y_centered ~ 0 + x_centered,
corr = corARMA(p=1, q=0),
data = dfIn
)
アプローチ2のみ試す。
D. 状態空間モデルとして定式化し、RのKFASパッケージを使ってカルマンフィルタで推定。おさらいすると、アプローチ2,5のモデルは
$y_t = \beta x_t + v_t$
$v_t = \rho v_{t-1} + e_t, \ \ e_t \sim N(0, \sigma_e^2)$
である。これを状態空間表現に書き換えよう。状態変数は$\beta$と$v_t$だと考え、縦に積んで$\alpha_t = [\beta, \ v_t]'$としよう。
観察方程式は
$Y_t = Z \alpha_t$
ただし $Z = [x_t, 1]$である。撹乱項がないことに注意。状態方程式は
$\alpha_t = T \alpha_{t-1} + R \eta, \ \ \eta \sim MVN(0, Q)$
遷移行列$T$は2x2の対角行列で、対角要素は$1, \rho$である。$R$は2x2の単位行列で、状態撹乱項は$\eta = [0, e_t]'$とする。共分散行列$Q$は2x2で、右下に$\sigma_e^2$がはいり、残りが0。
こいつをカルマンフィルタで推定する。Rコードはこんな感じ。遷移行列$T$に未知パラメータが入っているので、ちょっと面倒くさい。
library(KFAS)
mgZ <- array(dim = c(1, 2, nrow(dfIn)))
mgZ[1,1,] <- as.vector(dfIn$x_centered)
mgZ[1,2,] <- 1
oModel <- SSModel(
dfIn$y_centered ~ -1 + SSMcustom(
Z = mgZ,
T = matrix(c(1, 0, 0, 1), nrow = 2), # 最後の要素がrho
R = matrix(c(1, 0, 0, 1), nrow = 2),
Q = matrix(c(0, 0, 0, 1), nrow = 2), # 最後の要素がsigma_e
P1 = matrix(c(0,0,0,0), nrow = 2),
P1inf = matrix(c(1,0,0,1), nrow = 2)
),
H = matrix(0)
)
sub_update <- function(par, model){
# par: (sigma_eの対数, rho)
# model: 現在のモデル
model$T[2,2,1] <- par[2]
model$Q[2,2,1] <- exp(par[1])
return(model)
}
oFitted <- fitSSM(
oModel,
inits = c(log(var(dfIn$x_centered)/2), 0.5) ,
updatefn = sub_update,
lower = c(-10, -2),
upper = c(+10, +2),
method = "L-BFGS-B"
)
oEstimated <- KFS(oFitted$model)
計算の都合上$|\rho| < 2$と制約しているものの、このモデルは$|\rho| = 1$という仮定を置かないモデル、つまりアプローチ5ということになると思うのですが... 正しいでしょうか?
E. Mplusでベイズ推定。ここまではRなどという古くさい言語を使っておりましたが、いけてる分析者なら、ここは当然 Mplus ですよね! (すいません冗談です)
構造方程式モデリングの世界ではもはや標準となっているソフトウェア Mplus だが、実はN=1の時系列分析についても便利な機能を持っているのである。
Mplusのコードはこんな感じ。
DATA:
FILE = est2.dat;
VARIABLE:
NAMES = y x;
MISSING=.;
ANALYSIS:
ESTIMATOR = BAYES;
BITERATIONS = (2000);
MODEL:
v by (&1);
v;
v on v&1;
y on v@1 x;
[y@0];
y@0;
MODELコマンドがわかりにくいが、1行目は「vは潜在変数ですが指標を持っていません。モデルのなかでラグ1を使わせて下さい」。2行目は「その残差分散(つまり$\sigma_e$)を自由推定したいです」。3行目で$v_t$の自己回帰を定義し(v&1とは$v_{t-1}$を表す)、4行目で$y_t$のモデルを定義している($v_t$の回帰係数は1に固定している)。ほっとくと$y_t$の切片と残差分散を推定してしまうので、最後の2行でそれを抑止している。
このとき$v_t$の自己回帰係数($\rho$)は範囲が制約されていない、つまりアプローチ5だ、というのが私の理解なのだが、正しいだろうか...?
F. Stanでベイズ推定。ほんとはここまでやるつもりはなかったんだけど、毒も食らわば皿まで、ということで... Stanファイルはこんな感じ。
data {
int T;
vector[T] y;
vector[T] x;
}
parameters {
real beta;
real<lower=-1, upper =1> rho;
real<lower=0> sigma;
}
model {
vector[T] v;
v = y - beta * x;
v[1] ~ normal(0, sigma/sqrt(1-rho^2));
v[2:T] ~ normal(rho * v[1:(T-1)], sigma);
} 下から3行目、v[1]でなにか変なことを書いているが、これは$v_{t-1}$が未知であるときの$v_t$の周辺分布の分散が、$v_{t-1}$の下での$v_t$の条件つき分布の分散 $\sigma_e$より大きくなるからである。
どのくらい大きくなるかというと、
$v_t = \rho v_{t-1} + e_t$
の両辺の分散をとって
$Var(v_t) = Var(\rho v_{t-1} + e_t)$
$e_t$と$v_{t-1}$との共分散は0なので、
$Var(v_t) = \rho^2 Var(v_t) + \sigma_e^2$
ここから
$Var(v_t) = \sigma_e^2 / (1-\rho^2)$
である。
というわけで、尤度計算に当たってデータ点ひとつも無駄にしまいという質実剛健な精神に則り、v[1]についても誠意を込めて分布を書いてみたんだけど、でもこれって、$1-\rho^2 \neq 0$、つまり$|\rho| \neq 1$という仮定を暗黙のうちに含んでいないだろうか? そんならいっそ、というわけで、parametersブロックではreal <lower=-1, upper =1> rho; と書いた次第である。
このモデルとともに、parametersブロックでrhoの範囲制約をなくし、かつ下から3行目を消したモデルも推定してみた。前者はアプローチ2, 後者はアプローチ5に相当すると思うんだけど... うーーん、こういう理解で正しいのだろうか? からきし自信がない。
まとめると、出場選手は以下の10名である。
- A1: OLS推定, $\rho = 0$と仮定
- A3: OLS推定, $\rho = 1$と仮定
- B2: 最尤推定, $|\rho| < 1$と仮定
- B3: 最尤推定, $\rho = 1$と仮定
- B4: 最尤推定, 単位根検定に基づきモデル選択
- C2: FGLS推定, $|\rho| < 1$と仮定
- D5: カルマンフィルタ
- E5: ベイズ推定(Mplus)
- F2: ベイズ推定(Stan), $|\rho| < 1$と仮定
- F5: ベイズ推定(Stan)
推定の様子
この10人の選手に、11水準の$\rho$の各1000個のデータセットについて、$\beta$を推定させた。ただしStanは時間がかかるので、1000個のうち100個だけについて推定するだけで勘弁してやった。
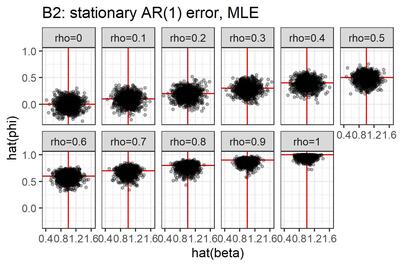
いったいなにをやっているのか、自分でもよくわかんなくなってきたので、選手B2(最尤推定, $|\rho| < 1$と仮定)による推定結果を図にしてみた。
点はデータセット、横軸は$\beta$の推定値, 縦軸は$\rho$の推定値である。真値が赤で表現してある。こうしてみると、真の$\rho$が1に近づくにつれ、$\rho$の推定値は0に向かって歪むみたいですね。横軸と縦軸の間にはあまり相関がなさそうだ。
さて、関心があるのは、$\beta$の真値すなわち 1 と、$\beta$の推定値$\hat{\beta}$とのずれである。その大きさを次の2つの指標で評価しよう。
- バイアス。$\hat{\beta}$の平均から1を引いた値。0に近くないと困る。
- RMSE、すなわち$(\hat{\beta}-1)^2$の平均の平方根。0に近いほうがありがたい。
結果
大変ながらくお待たせいたしました!お待たせしすぎたかもしれません! (ちょっと懐かしい冗談だ)
結果発表です!
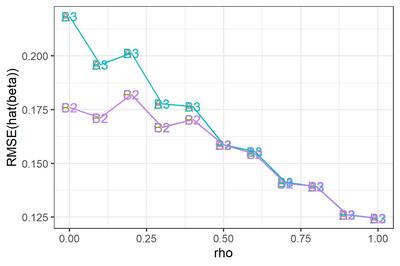
選手F2, F5のみ試行回数が100である点に注意。
シンプルなチャートだが、なかなか情報量が多いので、順にみていこう。
まずは、$\rho = 0$と勝手に想定し、OLS回帰をやってしまった場合。
真の$\rho$がそれほど大きくなければバイアスはそれほど大きくない。しかしRMSEは$\rho$とともに増大する。$\rho$が1に近づくと、バイアス・RMSEともに急増する。なるほど、撹乱項が非定常に近づいているわけだから、パラメータがうまく推定できないのも道理である。
やっぱりあれですね、時系列を分析する際には、きちんと自己相関を考慮することが大事ですね。
次に、$|\rho|<1$と決め打ちした場合(図のパネル2)と、$\rho=1$と決め打ちした場合(パネル3)について。バイアスはそれほど大きくないようだ。RMSEのみ拡大して示す。なお、選手F2はあとで観察することにして、ここでは省略する。
選手B2とC2, 選手B3とA3はぴったり重なってしまっている。つまり、$|\rho|<1$と決め打ちする場合、最尤推定するかFGLS推定するかにはたいしたちがいがないわけだ。$\rho=1$と決め打ちする場合に差分をとって最尤推定するかOLS推定するかも... そりゃそうか、きっと推定値は同じだ。
$\rho$が小さいとき、$\rho=1$と決め打ちするとRMSEが大きくなる。誤ったモデルを指定したわけだから、これは当然である。
これをみて大変に意外だった点がふたつある。
第1に、$\rho$が大きくなるにつれ、つまり撹乱項の自己相関が大きくなるにつれ、$\beta$のRMSEが小さくなっているという点である。$e_t$の分散が同じなら$\rho$が大きいほど撹乱項$v_t$の分散は大きくなるんだから、直感的には、$\beta$の推定はより難しくなるんじゃないかと思ったんだけど... なぜだろう???
もうひとつ、ふへええと言葉にならないため息をついたのは、$\rho$が1に近づくほど、$|\rho|<1$と仮定して定常AR(1)撹乱項を持つ回帰モデルを推定しても、$\rho=1$と仮定して差分時系列について回帰モデルを推定しても、違いがなくなってしまう点である。さきにみたように、単位根検定がしくじりやすいのは$\rho$が1に近いときである。そういうときほど、実は間違えたところでたいした実害はないわけだ。
このように、単位根検定でモデルを切り替えようが、頭から$|\rho|<1$と信じこんで定常AR(1)撹乱項を持つ回帰モデルを使い続けようが、ほとんどちがいがないようだ。たとえ$\rho=1$だったとしても、である。
ええええ? わざわざ単位根検定をやったのに、意味なかったわけ...?
最後に、$\rho$の範囲について制約しないモデル。
元の図にもどると、選手E5がとんでもないバイアスを持っていることがわかる。どうしたんだMplus! しっかりしろ! 医者だ、医者を呼べ!!
... 冗談はともかく、ひょっとすると私がコードを間違えているのかもしれない。残念ながらMplusくんは休場とし、他の選手についてRMSEを拡大してみよう。
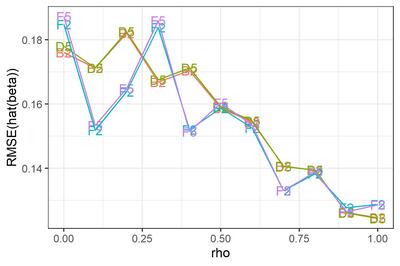
選手D5 (カルマンフィルタ) について。参考のために選手B2 (最尤推定) と並べてみた。ほとんど変わらない。
恥かしながらわたくし、撹乱項の定常性を仮定しているB2は$\rho=1$に近づくとだめになるが、定常性を仮定していないD5はうまくいく... という結果になるかな、と思っておりました。不明を恥じる次第であります。へええ、そうなのかー。
選手F5(Stanでベイズ推定)について。D5との優劣ははっきりしない。参考のためにF2 ($|\rho|<1$と仮定してStanでベイズ推定)と並べてみたところ、$\rho$が小さいところではF2が僅差で勝つが(そりゃそうだ、F2は正しい制約を追加しているわけだから)、$\rho$が1に近づくと僅差で負けるようだ。
まとめ
というわけで、シミュレーションの結果わかったことをまとめておくと、
- Q1. 時系列回帰モデル$Y_t = \alpha + \beta X_t + V_t$において、撹乱項$V_t$が高い自己相関を持つとき、$\beta$の推定誤差は大きくなるか、それとも小さくなるか。→小さくなる。
- Q2. $V_t$の自己回帰係数が1であるのにそれと知らず、1未満と仮定するモデルを推定したとき、$\beta$の推定誤差は大きくなるか。→ならない。
ううむ。どちらも意外な結果であった。勉強が足りないようだ。
それにしても、単位根検定の意味ってなんだろう? 時系列分析の教科書には必ず書いてあるけど、やっても意味なくない? ... と思ってしまったのだが、これは私が「時系列回帰で回帰係数を推定する」という場面だけに焦点を絞っているからで、たとえば予測に関心があるなら話はちがうのかもしれない。
それに、ここでは説明変数時系列が定常であると知っている場合について考えているが、もしそうでなかったら、そりゃあまあ単位根があるかどうか知りたいですわね、みせかけの回帰が怖いから。そういう意味でも、単位根の有無を調べることは、やはり大事なのでありましょう。
なお、この記事のために書いたコードはすべてGithubにアップしております。自己満足もいいところだがな!
2020/03/16追記: 先週書いたこの記事を見直して、はっと気が付いたので記録しておく。
お題は次の通りである。
$y_t = \beta x_t + v_t$
$v_t = \rho v_{t-1} + e_t, \ \ e_t \sim N(0, \sigma_e^2)$
というAR(1)誤差回帰モデルで、$\rho$が大きくなるほど$\hat{\beta}$のRMSEが小さくなるのはなぜか?
2本目の式をラグ演算子$L$を使って書き直すと
$v_t = \rho L v_t + e_t$
$(1-\rho)L v_t = e_t$
ラグ多項式$(1-\rho)L$を$R(L)$とし、
$R(L) v_t = e_t$
と書くことにする。$|\rho| < 1$なら$R^{-1}(L)$が定義できて
$v_t = R^{-1}(L) e_t$
1本目の式に代入して
$y_t = \beta x_t + R^{-1}(L) e_t$
両辺に$R(L)$をかけて
$R(L) y_t = \beta R(L) x_t + e_t$
これは($\rho$を既知とすれば)通常のOLS回帰と同じなので、$x_t^* = R(L) x_t$と略記して
$\displaystyle Var(\hat{\beta}) = \frac{\sigma^2_e}{\sum(x_t^* - \bar{x}^*)^2} $
である。つまり、AR(1)誤差回帰モデルの回帰係数の標準誤差は、ふつうの単回帰のように「撹乱項の分散と独立変数の偏差平方和の比」なのでなく、「AR(1)誤差の裏にあるホワイトノイズの分散と、$x_t - \rho x_{t-1}$の偏差平方和の比」なのである。だから、自己回帰係数が大きいほど分母は大きくなり、$\hat{\beta}$のSEは小さくなるわけだ。うっわー。
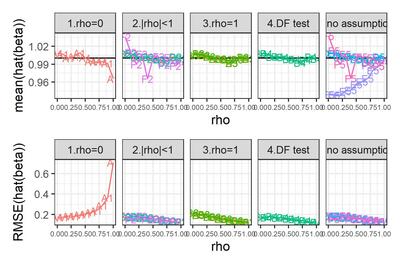
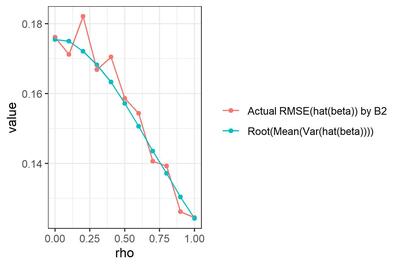
オレンジ色は、選手B2による$\hat{\beta}$の、真値($\beta=1$)に対するRMSE (再掲)。青色は、各試行について真の$\rho$を既知として$Var(\hat{\beta})$を求め、試行を通じて平均して平方根をとった値。
な・る・ほ・ど...