マーケティング・リサーチの重要な課題のひとつは,製品に対する消費者の好みを定量的に捉えることです。ここで問題になるのは,たとえひとりの消費者に注目したとしても,その好みは一種類ではなく,状況によって変動することがある,という点です。ニューヨーク市立大のジャック・リーたちは,消費者の複数の好みを定量的に表現する方法として「多重理想点モデル」を提案しています。この方法を用いると,個々の消費者の購買履歴データだけを用いて,その消費者の複数の好みを定量的に表すことができます。
ジョイント空間に基づく製品選択モデル
マーケティング・リサーチでよく用いられるツールのひとつに「プロダクト・マップ」があります。プロダクト・マップとは,製品が散らばっている架空の空間です。各製品が占めている位置は,その製品に対する消費者の知覚をあらわしています。たとえばこの論文では,粉末ジュースについてのプロダクト・マップをつくっています。オレンジとレモネードが近い位置にあり,別の場所には,フルーツパンチ,チェリー,ベリー,グレープが固まっています。前者は柑橘系の製品,後者は甘い製品だと解釈できます。
この空間の上に消費者の好みを重ね描きすることもできます(これを「ジョイント空間」と呼びます)。空間上で好みをあらわす方法には,消費者が好きな方向を示す矢印(理想ベクトル)を描き込む方法や,理想的な製品を表す点(理想点)を描き込む方法があります。理想点は,「理想点に近い場所にある製品は好まれやすい(ないし,選ばれやすい)」ということを表します。理想ベクトルや理想点は,消費者の全体的な好みを表すためにも,個別の消費者の好みを表すためにも利用できます。
適切なジョイント空間は,消費者の選好についての理解を深め,マーケティング戦略立案の基盤として役立ちます。その応用例のひとつに,ジョイント空間を基盤として消費者の製品選択を説明する数理モデルを構築する,というアプローチがあります。日本では片平(1990)のモデルが有名です。
単一選好モデルの問題点
ところが,ジョイント空間による表現には次のような問題点があります。たとえば実際の購買においては,自分の好きな製品を買う場合もあれば,家族の好きな製品を買う場合もあるでしょう。個人レベルの選好においてさえ,すっきりしたいときにはレモネード,小腹が空いたときにはフルーツパンチ...という風に,購買時の状況に応じて好みが変動する可能性があります。このように,ある消費者の好みは一種類とは限りません。
消費者の好みが本当は複数種類あるのに,それを無視したジョイント空間をつくってしまうと,この空間において表現されているのは消費者の平均的な好みに過ぎないことになります。このような空間では,消費者の間の違いを捉えるのは難しいですし,実際の製品選択を説明するのも難しくなります。
多重理想点モデル
この問題を解決するために,この論文は「多重理想点モデル」を提案しています。このモデルでは,個別の世帯・個人が複数の理想点を持つことができます。実際の選択場面では,そのなかのひとつの理想点が「活性化」します。どの理想点が活性化するかは確率的に決まります。ここで著者らは,「前に活性化した理想点によって,次の理想点の活性化の確率が変わる」という関係があり,この関係のタイプが世帯・個人によって異なるのだ,と想定しています。たとえば,毎回ちがう製品を買いたがる人(バラエティ・シーキングの傾向が高い人)は,このモデルでは「前に活性化した理想点と異なる理想点が活性化しやすい」タイプの人として捉えられるわけです。
著者らの方法の特徴は,各世帯(ないし個人)ごとの購買履歴データさえあれば,その世帯(個人)の理想点の数と位置を推定することができる,という点です。近年ではスキャン・パネル・データ(店頭や家庭に機器を置いて購買を記録したデータ)から購買履歴を簡単に手に入れることができますから,利用範囲の広い手法であるといえます。
適用例
著者らは粉末ジュースの購買履歴データにこのモデルを適用し,他のモデルに対する優位性を示しています。著者らが挙げている事例をひとつ紹介しましょう。
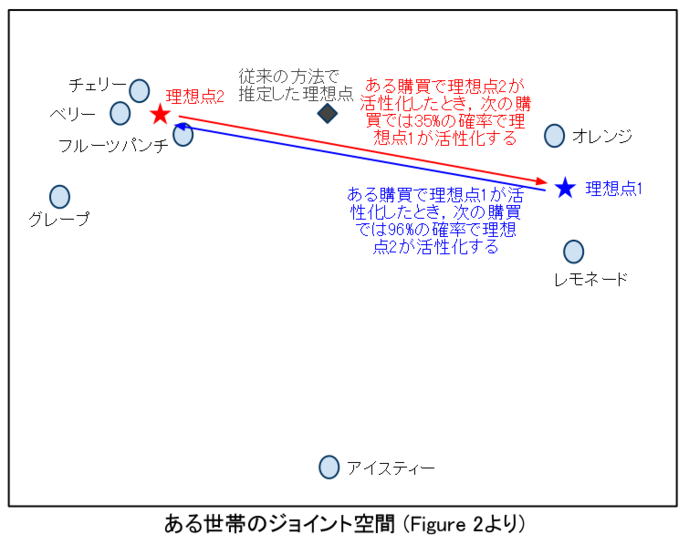
ある世帯は,粉末ジュースを66回購入していました。その内訳は,フルーツパンチ26回,オレンジ11回,チェリー10回...などで,いっけん様々な製品を脈絡なく買っているように見えます。 従来の理想点モデルを当てはめると,この世帯の理想点は,柑橘系ジュースと甘いジュースの中間に位置すると推定されました。
いっぽう,著者らの多重理想点モデルを当てはめると,この世帯は二つの理想点を持っていると推定されました。すなわち,オレンジに近い理想点とフルーツパンチに近い理想点です。 購買に際しては,27%の確率で前者,73%の確率で後者が活性化する,と推定されました。さらに,ある購買において前者の理想点が活性化すると,次の購買では96%の確率で後者の理想点が活性化する,という関係があると推定されました。この結果は,この世帯にとってオレンジやレモネードは「時々買いたくなるけれど2回続けて買おうとは思わない」ジュースである,と解釈できます。
今週はちょっと古い論文のご紹介です(何卒ご容赦ください)。題名のとおり,個人(ないし世帯)が複数の理想点を持つ理想点モデルを提案した論文です。
一読してとても意外だったのは,このモデルは従来の理想点モデルと同じく,本質的にはある個人についてのモデルであるという点です。つまり,製品の位置の推定を別にすれば,ある世帯の理想点はその世帯の購買履歴データだけを用いて推定されています。市場における理想点の分布についての確率モデルを構築するわけではないのです。この点でこのモデルは,コンジョイント分析において選好構造の異質性を捉えるために用いられているモデル(潜在クラスモデルや階層ベイズモデル)とは大きく異なります。
このようなアプローチは,各個人(世帯)についてのリッチな情報が手に入ることが前提になると思います。世の中にスキャン・パネル・データがあるからこそ成り立つ提案であって,いわゆる消費者調査データを使った分析では,ちょっと真似できないアプローチだなあ,とうらやましく感じました。
Lee, J.K.H, Sudhir, K., Steckel, J.H. (2002) A multiple ideal point model: Capturing multiple preference effects from within an ideal point framework. Journal of Marketing Research, 39(1), 73-86.
要旨
従来の研究では,世帯・個人はある製品カテゴリに関して複数の選好を持つ可能性があるということが示唆されてきた。こうした多重的選好が生じるのは,ある世帯に複数の個人が属しているせいかもしれないし,用途と使用オケージョンが異なるからかもしれないし,バラエティ・シーキングのせいかもしれない。従って,単一の不変な理想点を想定する単一理想点モデルは,誤った想定に基づいているといえるだろう。我々は,こうした多重選好の効果をうまく捉えることができる多重理想点モデルを提案する。このモデルの基本的前提は,消費者は理想点の集合を持ち,個々の理想点は異なる選好を表現する,というものである。任意の購入オケージョンにおいては,これらの理想点のうちひとつが,なんらかの確率で「活性化」され,その理想点の特性に基づいて選択が行われる。我々は本論文で,多重理想点モデルとその推定手続きについて,モデルが真の選好構造を復元できるかどうかという観点から評価する。次に我々は,粉末ソフトドリンクについてのInformation Resource Inc. のパネルデータに基づき,モデルを実証的に検証する。その結果について考察し,将来の研究の方向について紹介する。
(イントロダクション)
理想点モデルは消費者の選好が単一であると想定しているが,この想定は往々にして正しくない。我々は,世帯選好の内部分析・外部分析のためのモデルとして多重理想点モデル(MIPM)を提案する。MIPMは製品スイッチング行列を入力とするので,標準的なスキャナ・パネル・データが利用できる。MIPMは,ある世帯が複数の理想点を持つと仮定する(その理由は問わない)。それぞれの選択場面ではいずれかの理想点がなんらかの確率で「活性化」する。
1. 既存モデルと関連手法の概観
1.1 世帯レベルでの多重理想点の源流
- Gupta & Steckel(1993): 世帯データから個人の選好の状況を復元しようとした。
- 選好の多重性を説明するために,使用状況の分類が開発され,状況特定的な理想点の可能性が検討されてきた。
- バラエティ・シーキングのモデル。
1.2 理想点モデル
- 理想点モデルの推定のためのMDS手法。
- 理想点モデルとジョイント空間マップを,多様な形式のデータをつかって推定しようという試み(選好データ,選択データ,購買データなど)。
- 変動する選好に基づく選択行動の,マップに基づくモデル。
1.3 潜在クラス選好モデル
- 選好のセグメンテーションにおける潜在クラスモデルの適用。
- MDSに対する潜在クラスモデルの適用(LCMDS)。
- 選択オケージョンごとに異なる選好構造が呼び出されるという考え方として...
- Wedel&Seenkamp(1989,1991): fuzzy clusterwise regression
- Paulsen(1990): 潜在マルコフモデル
2. MIPM
(※以下,数式はlatex記法で記述)
2.1 単一理想点モデルの収集
複数の理想点が存在し,それぞれの選択オケージョンごとにいずれかの理想点が活性化すると考える。次元 a における理想点 k の位置を IP(k)_a , 選択肢 i の位置を i_a とする。理想点 k が活性化しているときに選択肢 i が選択される確率は
P[i|IP(k)] = (1/\sqrt{ \sum_a (i_a - IP(k)_a)^2 }) / (分子の全選択肢での合計)
とりあえずユークリッド距離を使うが,そうでなくても良い。
2.2 理想点遷移のモデル化
理想点のスイッチを単純1次マルコフモデルとして捉える。現在の理想点が k であるとき,次の理想点が l である確率を p_{kl} とする。バラエティ・シーキングは,遷移確率行列の対角成分 p_{kk} が小さい場合である。
2.3 スイッチングの確率
理想点 k が活性化している定常状態確率は
P[IP(k)] = \sum_l p_{lk} P[IP(k)]
さて,いま理想点 k が活性化しているとすると
- いまiを選ぶ確率は P[i|IP(k)]
- 次の理想点が l となる確率は p_{kl}
- 次の理想点が l であるときに j を選ぶ確率は P[j|IP(l)]
- 従って,(次の理想点を問わず) 次に j を選ぶ確率は \sum_l p_{kl} P[j|IP(l)]
従って,(理想点を問わず) 「i, 次に j」を選ぶ確率は
P(ij) = \sum_k { P[IP(k)] P[i|IP(k)] \sum_l p_{kl} P[j|IP(l)] }
2.4 推定手続き
消費者の選好には異質性があるが,市場の知覚は等質だと考えることにする。選択肢の位置 i_a は下記の方法で推定してもいいし(内部分析),別のデータを使っても良い(外部分析)。
上記モデルの尤度関数をつくって反復推定する。推定に必要なのは,個人ないし世帯レベルでのスイッチング行列(世帯ごとの遷移頻度 R(ij) )だけである。収束判定にはCAICを使う。次元数 A , 理想点数 L は事前知識なりCAICなりで決める(多くすると計算が大変になる)。
3. シミュレーション
推定量の特性を調べるためにシミュレーションを行う。消費者数, 次元数, 製品数,購買系列長,理想点数を要因計画で動かし,製品と理想点について真の位置と推定された位置の差を求めた。結果はそれなりに頑健だった。
4. 事例
MIPMモデルを実データに適用し,結果を単一理想点モデルならびにWIPモデル(Desoete, Carroll & DeSarbo, 1986)と比較する。WIPモデルは多変量正規分布のもとで理想点の移動を許容するモデルである。
4.1 データ
粉末ソフトドリンクのスキャン・パネルデータを用いる。59世帯,世帯あたり32~307回購買。2/3を推定に用い,残りを妥当性チェックのために用いる。製品数7。
4.2 推定と妥当性チェックの結果
66%の世帯が複数の理想点を持つと推定された。 WIPモデルと単一理想点モデルをナルモデルとみなし,ベイジアン交差妥当化尤度法によってMIPMモデルと比較した。どちらのモデルと比べてもMIPMモデルのほうが優れていた。
4.3 遷移行列の次数
世帯ごとに,1次のスイッチング行列を仮定するモデルと0次のモデルを比較した。63%の世帯で,0次のモデルのほうが適切であった。(引用者注: の世帯は単一理想点の世帯が34%,複数理想点で0次マルコフ過程の世帯が19%,複数理想点で1次マルコフ過程の世帯が37%...ということであろうか)
4.4 世帯の例
世帯057は66回購買していた。1次,2理想点のモデルが推定された。理想点1の位置はシトラス,2の位置はフルーツポンチに近かった。定常状態確率は27%, 73%で,遷移確率は理想点1が二回続けて活性化しにくいことを示した(すぐに飽きるのであろう)。いっぽう,単一理想点モデルでは理想点は中間地点となり,WIPモデルでは理想点の分布は幅広い楕円となった。これでは意味をつかみにくい。
5. 累積レベルでの含意
得られた世帯ごとの理想点を平均リンケージ法でクラスタ化した。MIPMでは主に3つの凝集性の高いクラスタが得られた。いっぽう単一理想点モデルの場合は,クラスタの凝集性が低く,そこに製品が存在しないようなクラスタが得られ,シトラス付近にはクラスタが得られなかった。
6. 考察と結論
限界と将来の拡張:
- モデルの推定のためには長い購買系列データが必要だが,あまりに長いと定常性が失われる可能性がある。たとえば新製品の登場とか,製品の位置の変化とか。
- ある店舗で複数製品を同時購買した場合の扱い。遷移確率に影響を与える可能性がある(理想点の位置は変わらない)。
- どの理想点が活性化するかを説明する変数の導入(マーケティング・ミックス変数や心理的変数)。










