elsur.jpn.org >

« 2016年12月 | メイン | 2017年3月 »

2017年1月22日 (日)

　ここんとこ山のようなデータ整形を抱え込んでいて、これはほんとに終わるのかという不安と、こんなことをしていてよいのかという不安に両側から押し潰されそうだが... とにかく仕事があるだけありがたいと考えるべきか。
　ともあれ、ちょっと驚いたことがあったのでメモしておく。なんだか恥をさらしているような気も致しますが。

　Rで、ユニークなキーを持つとても大きなテーブルを左外部結合(LEFT JOIN)したいとき、どうするのが速いか。
　思いつくのは、

  1. 素直にmerge()する
  2. merge()より高速だといわれている, Hadley神つくりたもうた dplyr::left_join() を使う
  3. match()で行位置を探し、テーブルの行を並び替えてくっつける
  4. match()で行位置を探しておき、テーブルの各変数を ひとつづ並び替えてくっつける

　4番目のは一種の冗談のつもりであった。そんなん遅いにきまってるじゃん？ たぶん2,1,3,4の順だろう。いやひょっとして2,3,1,4かな。私はそう思いました。

　衝撃の結果は下図。クリックで拡大。Rpubsにものっけてみました。

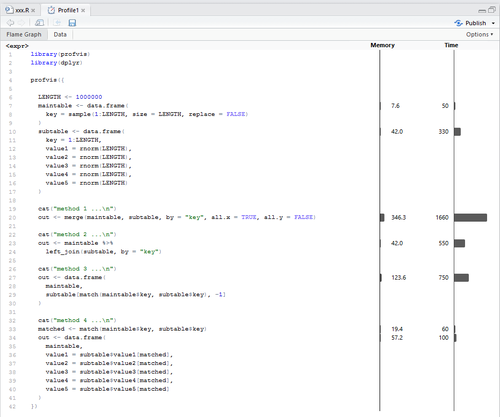
xxx.png

　4がぶっちぎりで優勝。ぐぬぬぬ。これまでの苦労は何だったんだ。

雑記：データ解析 - RでどうやってLEFT JOINするか (ああなんて最先端な話題だろうか)

2017年1月13日 (金)

Pan, Y., Caudill, S.P., Li, R., Caldwell, K.L. (2014) Median and quantile tests under complex survey design using SAS and R. Computer Methoss and Programs in Biomedicine, 117(2), 292-7.
　勤め先の同僚と話していて、そういえば標本ウェイティングの下での中央値ってなんだろう...と疑問に思い、適当に拾って読んでみた。

　えーと、Moodの中央値検定というのがある。
　母集団のサイズを$N$、母中央値を$M_N$、標本中央値を$M_n$とする。母集団が$C$個の下位母集団(subpopulation)に分かれていて、そのサイズが$N_1, \ldots, N_C$だとする。下位母集団$i$の標本[? 原文 "the ith sample"]の中央値を$M_i$とする。いま、
　$H_0: M_1 = M_2 = \cdots = M_C = M_N$
について検定したい [←あれ？ ちょっと変じゃない？ この式を信じるなら、$M_i$は標本中央値じゃなくて母中央値でないとおかしい]。
　下位母集団$i$の標本[? 原文 "the ith sample"]において、値が$M_N$以下のケースの数を$A_{1j}$、$M_N$より大のケースの数を$A_{2j}$とする。$A_{11} + A_{12} + \cdots + A_{1c} = (1/2)N$である。[←あ、やっぱりおかしい。著者のいう"the ith sample"というのは下位母集団のことなのだろうか？]
　$H_0$の下で、任意のケースが$M_N$を超える確率は0.5である。$M_n$を超える確率は超幾何分布になっちゃうんだけど、$n$が$0.1N$より小さければ$p=0.5$の二項分布で近似できる。[←この論文、数式の記法が滅茶苦茶わかりにくいな。$M_n$というのは「$n$番目の下位母集団の中央値」という意味じゃなくて全体の標本中央値のこと。$n$は標本サイズであろう]
　"the ith sample"における任意のケースが$M_N$以下となる確率を$P_i$とすると、
　$H_0: P_1 = P_2 = \cdots = P_C = 1/2$
と書き換えられる。これは$df=C-1$のカイ二乗検定で検定できる。
　これを分位数の検定に拡張するのは簡単で、$q$分位数について
　$H_0: P_1 = P_2 = \cdots = P_C = q$
とすればいい。

　これをcomplex sampleに拡張しよう。
　層$h$、クラスタ$a$における個体$i$の値を$y_{hai}$とする。面倒なので以下では$y_i$と略記する。ウェイトを$w_i$とする。
　母集団全体における$y_i$の分布を$F$とする。$q$分位数を$Q$とする。$y_i \leq y$のときに1となるインデクスを$I_y(y_i)$として、標本経験分布[標本CDFのことであろう]は
　$G(y) = \sum_i w_i I_y(y_i) / \sum_i w_i$
である。$P_i$の推定量は、個体$i$が下位母集団$c$に属しているときに1となるインデクスを$x_{i|c}$として、
　$p_i = \sum_i w_i x_{i|c} I_q(y_i) / \sum_i w_i x_{i|c}$
となる。[←あーもう！ $i$の意味が右辺と左辺で違うじゃん！ 下位母集団の添え字は別のを使うべきだよね]
　検定統計量は、まず$[p_1, p_2, \ldots, p_C]'$の共分散行列を、SASのproc surveyregなりRのsurveyパッケージなりで推定して... 云々... めんどくさくなってきたのでやめるけど、とにかく$df=C-1$でカイ二乗分布に従う検定量がつくれる由。
　
　後半は、著者らによるSASマクロならびにRプログラムの紹介。欲しければ連絡せよとのこと(webを探したけど見当たらなかった)。さらに、NHNEMというデータによる実例。どちらも読み飛ばした。

　。。。検定統計量の組み方はなんだかわからんが、要するに、ウェイティングした標本CDFを群ごとに描いたとき、特定の母分位点(たとえば母中央値)について、その不偏推定量をつくることなく、それが群間で異なるかどうかを検定する、ということだろうか。

　いやー、ゆうたらなんやけど、めっちゃわかりにくい論文だった。記号の使い方が滅茶苦茶である。ひょっとしてこれ、校正前の原稿かなにかなのだろうか。
　いまためしに検索してみたら、google scholar 的には被引用数0件。痺れる。たった数頁とはいえ、読むものは選ばんといかんなあ。

論文：データ解析(2015-) - 読了：Pan, et al. (2014) 標本ウェイティングの下で中央値や分位数について群間の差を検定する方法

2017年1月 7日 (土)

Enders, C.K., Tofighi, D. (2007) Centering Predictor Variables in Cross-Sectional Multilevel Models: A New Look at an Old Issue. Psychological Methods, 12(2), 121-128.
　仕事の都合で目を通した奴。階層線形モデルを組むとき、センタリングをどうするか、正直なところいまいち自信が持てず、毎回ちょっと迷う。気分が悪いので、一度まとまった解説を読んでみたいものだと思って手に取った次第。
　世間のみなさまが！ディープラーニングだ、人工知能だと騒いでおられるこのときにですね！私は「全平均引いたほうがいいのかな、群平均引いたほうがいいのかな」なんてささやかなことで悩んでおるわけですよ。取り残されてますね！

　著者いわく。階層線形モデルのレベル1説明変数のセンタリングについて、みんなよくわかってない。心理学のトップジャーナルにさえ誤用が頻発しておる。おまえらな、センタリングってのはデータで決まるもんじゃないんだよ、何に関心があるかで決まるんだよ。わかってんのかこら。[とは書いてないけど、まあそういうニュアンス]

　まずは説明用の例題から。
　レベル1を従業員、レベル2を組織とする。組織$j$の従業員$i$の幸福感$W_{ij}$と労働時間$H_{ij}$の関係について階層線形モデルを組むとしよう。幸福感と労働時間の関係は、どの組織内でみても負の相関、各組織について平均をとって組織間でみても負の相関だとする。
　レベル1のモデルを
　$W_{ij} = \beta_{0j} + \beta_{1j} H_{ij} + r_{ij}$
とする。$r_{ij}$の分散を$\sigma^2$とする。レベル2のモデルを
　$\beta_{0j} = \gamma_{00} + u_{0j}$
　$\beta_{1j} = \gamma_{10} + u_{1j}$
とする。一緒にして書けば
　$W_{ij} = \gamma_{00} + \gamma_{10} H_{ij} + u_{0j} + u_{1j} H_{ij} + r_{ij}$
である。$u_{0j}, u_{1j}$の分散と共分散をそれぞれ$\tau_{00}, \tau_{11}, \tau_{10}$とする。推定するパラメータは$\gamma$が2つ、$\tau$が3つ、$\sigma^2$、計6個ね。
　
　$H$を全平均センタリング(CGM)すると何が起きるか。
　当然ながら、$W$との相関はセンタリングしない場合と変わらない。$H$は群間の分散を持っている。$H$はレベル2の説明変数とも相関しうる(たとえば組織サイズ$S$が大きいと幸福度が低いとすると、労働時間が長いほうが幸福度が低いから、つまり労働時間が長いと組織サイズが大きいことになる)。
　切片$\gamma_{00}$はなにを表すか。レベル1のモデルは
　$W_{ij} = \beta_{0j} + \beta_{1j} (H_{ij} -\bar{x}_{H})+ r_{ij}$
変数を各組織の期待値に置き換えて
　$\mu_{W_j} = \beta_{0j} + \beta_{1j} (\bar{x}_{H_j} - \bar{x}_{H})$
つまり$\beta_{0j}$は、組織$j$の幸福感の平均を労働時間で調整した値になっている。$\gamma_{00}$はその平均だ。
　では、傾き$\gamma_{10}$はなにを表すか。$H$は群間の分散を持っているから、$\gamma_{10}$は組織内の幸福感-労働時間の相関と、組織間の幸福感-労働時間の相関の両方を反映する[←んんんん？ あとでよく考えてみよう]。つまり、$\gamma_{10}$はレベル1の効果の推定量になっていない。組織を無視して回帰モデルを推定したときの回帰係数と同じで、群内の回帰直線をプールした奴と群間の回帰直線の両方を反映し、解釈しにくい。
　分散$\tau_{00}, \tau_{11}$も解釈しにくい。というのは、上の式からわかるように、$\beta_{1j}$が大きいと$\beta_{0j}$は小さくなるわけで、$\tau_{00}, \tau_{11}$をそれぞれ単独では解釈できないし、[...よくわかんなかったので中略するけど...] $\tau_{00}$はゼロに向かってシュリンケージし、$\tau_{11}$は負の方向にバイアスがかかる。
　
　$H$をクラスタ内センタリング(CWC)すると何が起きるか。
　もはや$H$は群間の分散を持たない。$W$との相関はがらっと変わり、レベル2の説明変数とは相関しなくなる。
　切片$\gamma_{00}$はなにを表すか。レベル1のモデルは
　$W_{ij} = \beta_{0j} + \beta_{1j} (H_{ij} -\bar{x}_{H_j})+ r_{ij}$
$\beta_{0j}$は、組織$j$における幸福感の無調整な平均である。$\gamma_{00}$はそのまた平均、$\tau_{00}$はその分散である。$H$は群間の分散を持っていないから、$\gamma_{10}$はレベル1の効果の推定量になる。傾きと切片は切り離され、分散$\tau_{11}$はバイアスを受けない。

　CGMとCWCをどう使い分けるか。典型的な４つのケースについて考えよう。

　もしレベル1の説明変数が二値だったらどうするか。なんか変な気がするかもしれないけど、この場合も話は全く同じで、適切なセンタリングをすべきである。ダミーコーディング(0,1)でもイフェクトコーディング(-1,+1)でも全くおなじこと。

　... 自分の能力不足を棚に上げていいますけど... この論文の説明って、ちょっとわかりにくくないですかね？そんなことないですかね？
　勉強にはなったが、それと同じくらいに疑問も増えた。他の解説も読んでみよう。

論文：データ解析(2015-) - 読了：Enders & Tofighi (2007) 階層線形モデルで説明変数をセンタリングする正しいやり方

2017年1月 5日 (木)

　えーと、アメリカにMSI(Marketing Science Institute)というところがあって、年に2回、「実務家どもよ、最近の面白い論文はこれだ」というキュレーションをやっている。たまに目を通しては面白がったりうんざりしたりしてたんだけど、このたび都合によりメモをとってみた。
　2016年10月のおすすめ論文12本についてメモ。元論文の要旨にしか目を通していないので、タイトルも内容もいいかげんです。

消費者の支出を予測する新手法
Jang, S., Prasad, A., Ratchford, B.T. (2016) Consumer spending patterns across firms and categories: Application to the size- and share-of wallet. International J. Research in Marketing , 22, 123-139.
複数のカテゴリを扱っている企業が、競合の売上がわかんない状態で消費者の支出を予測するための方法。潜在クラスつきのトービット・モデルをつかいます(つまりセグメンテーションしながら各セグメントにトービットモデルを当てはめるってことね)、支出の異質性も扱えます、企業間・カテゴリ間での支出の相互関係も扱えます、カテゴリ支出がないことによる打ち切りも扱えます、とのこと。ああ... メモをとっていてようやく意味がわかった。これ、すごく役に立つ話かも...

「はい/いいえ」形式だと人はクリックしやすくなる
Putnam-Farr, E., Riis, J. “Yes/No/Not Right Now": Yes/No Response Formats Can Increase Response Rates Even in Non-Forced-Choice Settings. J. Marketing Research, 53(3), 424-432.
そうそう、これは読まなきゃと思ってた奴。メールでフィールド実験をやって、伝統的なオプト・インの設問とyes-no設問のCTRを比べる。強制選択でなくたって、yes-no設問だと反応率が上がるのよ、とのこと。

消費者の参加が新製品開発の役に立つ場合とそうでもない場合
Chang, W., Taylor, S. (2016) The Effectiveness of Customer Participation in New Product Development: A Meta-Analysis. J. Marketing , 80, 47-64.
表題についてのメタ分析。製品開発における消費者参加が上市までの時間を長くしてしまう場合がある、効く分野と効かないかない分野がある、というような話らしい。興味深い話ではあるが、なんかすごく面倒くさそうだ。

ブランド知覚のリアルタイム監視
Culotta, A., Cutler, J. (2016) Mining Brand Perceptions from Twitter Social Networks. Marketing Science , 35(3), 343-362.
いっかにも誰かがやりそうな話で、題名を見ただけでちょっと笑っちゃったんだけど...表題の通り、Twitterでブランド知覚を監視しますという話。200ブランド以上について3つの属性を監視したんだそうだ。ふーん。

「決定したことの喜び」が顧客経験を向上させる
Parker, J.R., Lehman, D.R., Xie, Y. (2016) Decision Comfort. J. Consumer Research . 43(1) 113-133.
意思決定の後で、その決定自体についての評価とか後悔とか満足とかとは無関係に、人はソフトにポジティブな感情(decision comfort)を持つことがあるよね。というわけで、測定尺度を作るわ、その帰結について検討するわ、実験を9個もやっている忙しい論文(ちょっとやりすぎじゃないですかね)。よくわかんないけど、著者らが提唱するdecision comfortとは、選択肢の比較に由来する感情ではなく、決定時の情動関連的手がかりに対する反応なのだそうです。配送費はサービスしますよとか、お客様その財布の柄ステキですねとか、そういう話だろうか？

ハッシュタグは「ブランド・パブリック」の登場を告げているのか？
Arbidsson, A., Caliandro, A. (2016) Brand Public. J. Consumer Research . 42(5) 727-748.
ブランド・コミュニティという概念があるけど、twitterの分析を通じて新たな概念「ブランド・パブリック」をご提案します、という論文。この雑誌には定性調査ベースの質的研究も載るんだけど、これもそういうのらしい。ブランド・コミュニティとのちがいは、(1)当該の関心事に焦点を当てていることによって形成されているだけで、相互作用に基づいているのではない、(2)議論ではなく感情で構造化されている、(3)ブランドはただの媒体に過ぎず、ブランドをめぐる集団的アイデンティティなんて形成されない。

「検索ビッグデータ」で競合マップを描く
Ringel, D.M., Skiera, B. (2016) Visualizing Asymmetric Competition Among More Than 1,000 Products Using Big Search Data. Marketing Science , 35(3), 511-534.
製品比較サイトの検索データから消費者の考慮集合と競合関係を導出します、という話。TV市場(製品数は1000を超える)で実例を示している由。なんと、第二著者は予測市場を研究してるSkieraさんだ。まじか。

ネットの評価は製品のほんとうの品質を表すか？
de Langhe, B., Fernbach, P.M., Lichtenstein, D.R. (2016) Navigating by the Stars: Investigating the Actual and Perceived Validity of Online User Ratings. J. Consumer Research , 42(6), 817-833.
1200以上の製品についてのネット上のユーザ評価を調べたところ、信頼あるConsumer Reports誌のスコアとは全然一致せず、よく見るとサンプルサイズは小さすぎ、リセール価格をも反映せず、プレミアムブランドで高くなってました。ユーザ評価への消費者の信頼は幻想に基づいております。というような内容らしい。はっはっは。先生方、夜道に気を付けたほうがいいですよ、IT企業の刺客がやってきますよ。

売上に対するネットクチコミの影響
Rosario, A.B., Sotfiu, F., de Valck, K., Bijmolt, T.H.A. (2016) The Effect of Electronic Word of Mouth on Sales: A Meta-Analytic Review of Platform, Product, and Metric Factors. J. Marketing Research , 53(3) , 297-318.
これもメタ分析。ネットクチコミと売上との相関は+.091、プラットホームによっても製品によっても大きく違う。クチコミの中身よりも量のほうが効く。云々。

オンデマンド・ストリーミング・サービスと音楽産業：Spotifyの教訓
Wlomert, N., Papies, D. (2016) On-demand streaming services and music industry revenues — Insights from Spotify's market entry. International J. Research in Marketing . 33(2), 314-327.
Spotifyみたいな定額or広告ベースの音楽サービスは、ダウンロード販売やCD販売とカニバるか？というのを大規模な縦断調査で調べた由(おお、調査手法がすごいっすね)。無料サービスはやっぱしネガティブな効果を持つけど、有料サービスまで含めて考えるとポジティブである由。

キャンペーンでマルチチャネル購買者を増やせるか？
Montaguti, E., Neslin, S.A., Valentini, S. (2016) Can Marketing Campaigns Induce Multichannel Buying and More Profitable Customers? A Field Experiment. Marketing Science , 35(2), 201-207.
マルチチャネル購買者は利益率が高いといわれているんだけど、じゃあどうすればマルチチャネル購買者を増やせるか。ランダム化フィールド実験をやった(まじか。すげえな)。結果、マルチチャネルでの買い物の利点を訴求する(金銭的インセンティブには頼らない)キャンペーンがうまくいった。傾向スコアでマッチングして、マルチチャネルだとやっぱり儲かるということが示せた。云々。

オンラインデータでTVについて予測する
Liu, X., Singh, P.V., Srinivasan, K. (2016) A Structured Analysis of Unstructured Big Data by Leveraging Cloud Computing. Marketing Science . 35(3), 363-388.
SNSみたいなオンラインデータから、TV番組の視聴率(?)をどうにかして予測しましょう、という話。使うのはtwitterだけど、事前にトピックを決めといて関連ツイートの量を追いかけるんじゃなくて、機械学習で事後的に分類する由。それは面白そうですね。これ、論文の題名が不親切だよな...

　こうしてメモをとってみて気が付いたけど、MSIのキュレーションって、結構ミーハーかもしれない。もっと地味だけど大事な研究もあるような気がする。

雑記 - MSIが選ぶマーケティング論文：2016年秋

Simkin, M.V., Roychowdhury, V.P. (2003) Read Before You Cite! Complex Systems, 14(3).

　かつてフロイトは精神分析学を言い間違いに適用してヒトの心理を暴いた。このたび我々は統計分析をミスプリに適用し、論文の著者が引用文献をほんとに読んでいるかどうかを暴く方法を開発しました...という論文。はっはっは。

　たとえば、ある有名な物理学の論文を引用している論文を4300本集めたところ、引用文献の際にミスプリがあるのが196本。ところがミスプリの異なり数は45種類で、一番メジャーなミスプリは78本もの論文でみつかった。誤りがコピペで伝染しているのだろう。縦軸に頻度の対数、横軸に頻度のランクの対数をとってミスプリの種類をプロットすると綺麗な直線となる。つまりZipf法則に従っているわけである。

　大雑把に考えると...
　ミスプリの総数を$T$、ミスプリの異なり数を$D$としよう。$T-D$人の引用者は他の人が書いた書誌情報をコピペしている、つまり実は読んでないと考える。$D$人の引用者は、まあ書誌情報にはミスプリがあるけど推定無罪ってことにすると、$T$人中$D$人が読んだ人。この比率は、ある論文の引用者に占める、その論文をほんとに読んだ人の割合$R$を近似していると考えられる。

　もうちょっときちんと考えると...[ここから本格的に数式が入ってくる。基本的なアイデアは上と変わんないと思うので略]
　というわけで、ある文献の引用者のうちその文献を読んでいるのは20%程度ではないか。云々。

　後半の肝心なところは読み飛ばしたけど、まあ、よしとしよう。発想が面白いっすね。
　それにしても、この話の肝になるのは、引用文献の書誌情報に伝染性のミスプリがあったらその文献を読んでない、という仮定である。著者らの言い分はこうだ。「原理的には、著者は引用を信頼できない文献リストからコピーしたが、その論文はちゃんと読んでいる、と主張することも可能かもしれない。しかし普通に考えれば、そんなのは比較的に稀で、ほとんどの場合にはあてはまらないと思われるだろう」。
　うーん、そうかなあ。文献管理ソフトをつかっていると、(1)欲しい文献の書誌情報を入力し(既存文献からのコピペで)、(2)その文献を手に入れて読み、(3)自分の原稿で引用したら、最初にいれた書誌情報が反映されちゃった...というようなことがありがちだと思うんですけど？ ついでにいうと、著者が自分の過去論文を引用してて、その書誌情報が間違っている、というのも見たことあるんですけど？
　著者らもここが弱点だという認識があるようで、いわく、この論文で言う「読者」とは、引用文献リストを作る際にオリジナルの論文や信頼できるデータベースを参照した人のことだ、と断っている。

論文：データ解析(2015-) - 読了：Simkin & Roychowdhury (2003) 論文を引用している人のうち何割がその論文をほんとに読んでいるかを推定する

2017年1月 4日 (水)

Bookcover シェイクスピア全集24 ヘンリー四世 全二部 [a]
シェイクスピア / 筑摩書房 / 2013-04-10
以前に小田島訳で読んでいたのだけど(ブログを検索してみると2011年だ)、このたび松岡訳で再読。

　ヘンリー四世といえば不肖の王子ハルとほら吹きフォルスタッフである。以前戯曲を読んだときは、フォルスタッフの魅力にただ打ちのめされるだけだったが、このたび付き合いで舞台を観て(鵜山仁演出)、遊蕩のハル王子がなにを考えておるかという点が、はじめて腑に落ちるような気がした。もちろん、いろんな解釈がありうるんだろうけど...
　思うに、ハルくんは自分が何者なのか、なにをしたいのか、よくわかってないし、わかりたくないんじゃないですかね。一部三幕で父王に叱責されたハルは、心を改めますと誓い、ホットスパーと闘いますと宣言するけれど、そういう自分の言葉を自分でも信じきれないんじゃなかろうか。ついでにいうと、父王もまた、最期まで息子を信じてないんじゃないんじゃないかと思う。それでも死の間際、父は息子を許すのだけけれど。
　そう考えると、最後にフォルスタッフを冷たくあしらうくだりも、思ったほどには哀しい場面ではないような気がしてくる。人はいつか、自分が何者かを知り、状況の軛のなかで生きなければならない。もしかすると、遊蕩の師・フォルスタッフにも、その結末はうすうす分かっていたのかもしれない。

フィクション - 読了：「ヘンリー四世」

Bookcover 浄土三部経〈上〉無量寿経 (岩波文庫) [a]
中村 元,紀野 一義,早島 鏡正 / 岩波書店 / 1990-08-16
Bookcover 浄土三部経〈下〉観無量寿経・阿弥陀経 (岩波文庫) [a]
中村 元,紀野 一義,早島 鏡正 / 岩波書店 / 1990-12-17
　えーっと、浄土三部経とは、無量寿経、観無量寿経、阿弥陀経、を指すのだそうです。
　なにかの気の迷いでフラフラと買っちゃった本なんだけど、それはそれで興味深い内容であった。ような気がする。サンスクリット語ないし漢文からの和訳しか読んでなくて、漢文書き下ろしのほうは飛ばしちゃったので、読み終えたとはいえないかもしれないけど。
　しっかし、極楽浄土って黄金や宝石であふれているのね。どうやら比喩ではないらしい。びっくりした。解説によれば、浄土経典が成立したインドのクシャーナ王朝時代は、金貨の流通量がもっとも多かった時期で、ここに出てくる極楽浄土は、当時の富者の生活の誇張表現なのだそうである。

哲学・思想(2011-) - 読了：「浄土三部経」

年末年始で読んだ本。

Bookcover 欧州複合危機 - 苦悶するEU、揺れる世界 (中公新書) [a]
遠藤 乾 / 中央公論新社 / 2016-10-19
ダメモトで読んでみたんだけど、私のようなど素人にもわかりやすく、興味深い内容であった。
　著者の先生いわく、このたびの難民危機に対する反応を指して、EUの理念は地に堕ちたと人はいうけれど、もともとEUは移民の流入に対し警戒的であった。弁護するわけじゃないけど、一度入境した人に対してはできるだけEU市民に近い扱いを心掛けていた、ということにも目を向けないといけない。

ポスト・ナチスの人権時代にあって移民に直面する国家のほとんどは、それがリベラルでありつづける以上、アイデンティティのありかを自由と平等を重んずるリベラリズムに求めざるを得ないという一見奇妙な状況が現出しつつある。たとえば、ジハード主義的な価値観と対峙する際、[...] 当該国のナショナルな価値として持ち出されるのは、ジェンダーの平等や同性愛の認知といった、いたって普遍的なリベラルな価値である。こうした傾向は[...]当該国のアイデンティティをリベラルに再定位するのである。
デモクラシーは、原理的にも歴史的にも一定の領域と構成員を前提としている。[...]寛容なデモクラシーは、それ自体領域とメンバーシップの安定を要請する。とくにメンバーシップが移民の時代にあって領域より流動化しやすいなか、それは自身の寛容さを守るため、メンバーシップを管理する(つまり一定の不寛容さを示す)という倒錯した必要が生じることになる。

上の引用箇所で、ヨプケ「軽いシティズンシップ」(岩波書店)という本が紹介されていた。忘れないうちにメモ。

Bookcover ホッブズ――リヴァイアサンの哲学者 (岩波新書) [a]
田中 浩 / 岩波書店 / 2016-02-20

Bookcover 贖罪のヨーロッパ - 中世修道院の祈りと書物 (中公新書) [a]
佐藤 彰一 / 中央公論新社 / 2016-11-16

Bookcover 消えゆく「限界大学」:私立大学定員割れの構造 [a]
小川 洋 / 白水社 / 2016-12-28
私恨を晴らすタイプの本ではなくて、データに基づく真面目な本なんだけど、弱小私大の経営陣・教員の悲惨な実像について縷々語るくだり(5章)で、記述がやたらに生き生きとしてくる...

ノンフィクション(2011-) - 読了：「欧州複合危機」「ホッブズ」「贖罪のヨーロッパ」「消えゆく限界大学」

« 2016年12月 | メイン | 2017年3月 »

rebuilt: 2020年11月16日 22:40
validate this page