elsur.jpn.org >

« 2014年2月 | メイン | 2014年4月 »

2014年3月30日 (日)

　このブログの趣旨に反して、これから書くのは私の覚え書きではなく、他の方に読んでもらうための文章である。どうか私が事柄を正しく説明していますように。そしてこのエントリが、検索結果の上の方に出てきますように。

　市場調査に関連する仕事で糊口を凌いでいるのだけれど、折々に受ける業務上のご質問のなかでかなりの領域を占めているのが、いわゆる「ウェイトバック集計」、すなわち確率ウェイティングに関するあれこれである。
　もっとも基本的な質問はこういうのだ。「ウェイトバックしたほうがいい？しないほうがいい？」 これはですね、ほんとに答えに困ります。

　いま手元に標本抽出確率が不均一な標本があり、集計・分析の際にウェイティングすべきかどうかが問われたとき、考慮すべきポイントは、主に4つあると思う。

　(1) については誤解がないと思う。(2)についてはいろいろ誤解があり、以前義憤に駆られて思うところを書いた。(4)は話がすごく長くなる。
　問題は(3)である。実のところこの論点こそが、調査実務に関わる人にとっての道しるべ、ウェイティングの是非という難しい問題に光を差してくれる灯火となると思うのだけれど、不思議なことに、この点についてきちんと説明した日本語の資料をほとんどみたことがない。同業種の方々と話していても、誠に失礼ながら、この点についてきちんと理解しておられる方は非常に少ないように思う。あまりに少ないので、ひょっとして私が全てを勘違いしているのではないかと不安になるほどだ。
　(3)について誰かに説明しなければならない羽目に陥ることもある。これが結構大変なのである。できれば避けて通りたい。いまはなんでも検索する時代だから、いちど文章にしてブログかなにかに書いておけば、そのぶん説明の回数も減らせるかもしれない。もし私が全てを勘違いしているのならば、それを指摘してくださる奇特な方が現れないとも限らない。
　以上が、この文章を書く主たる理由である。実はもうひとつ、ついうっかりwebアプリをつくってしまったというささやかな理由もあるのだけれど、それはあとで。

問題
　以下では、いわゆる「ウェイト・バック集計」、すなわちデータの集計・解析における確率ウェイティングについて考える。上記の4つのポイントのうち(1)(2)(4)はすでにクリアされていることにする。
　調査データの解析で確率ウェイティングが登場する局面は意外なほど多岐にわたるのだけれど(Kish(1990)は7種類挙げている)、説明に際しては、もっともわかりやすくて一般的な、非比例の層別抽出を想定する。集計対象は二値変数で、母集団全体における割合に関心があることにする。母集団は十分に大きいことにする。

　あまりにシンプルすぎて非現実的ではあるが、次の場面について考えよう。ある新製品コンセプトに対する消費者の購入意向を調べたい。そこで潜在的顧客から抽出した調査対象者に、その製品を買ってみたいどうかを「はい/いいえ」で聴取した。以下、「はい」と答える人の割合のことを購入意向率と呼ぶことにする。
　性別で層別した標本抽出を行った。つまり、男と女のそれぞれについて、決まった数の調査対象者を得た。潜在的顧客における男女比は5:5であることがわかっている。しかしなにかの事情があって、調査対象者は男60人、女40人とした(男女比は6:4)。これらの対象者は、その性別のなかでは無作為に抽出されたものとみなすことにする。

　いま知りたいのは、潜在的顧客(母集団)の全体における購入意向率である。その推測の手段として、調査対象者(標本)から得た回答を集計し、購入意向率を算出する。
　ここでunweightedの集計値とは、「はい」と答えた人の人数を100で割った値である。
　いっぽうweightedの集計値は次のように説明できる。男60人における購入意向率、女40人における購入意向率をそれぞれ求め、得られた2つの値を、母集団における割合(ここではそれぞれ0.5)で重みづけて合計する。これがweightedの集計値である。
　あるいは次のようにいいかえてもよい。まず各対象者に適切な「ウェイト」を与える。たとえば、男性の対象者には5/6=0.833, 女性の対象者には5/4=1.250というウェイトを与える。次に、「はい」を1点、「いいえ」を0点とし、各対象者の持ち点にウェイトを掛けて合計し、最後にウェイトの合計で割る。これがweightedの集計値である。

　さて、unweightedの集計値とweightedの集計値、どちらを使うべきか。ウェイティングすべきか、すべきでないか。

　たいていの人はこう答える。ウェイティングすべきです。なぜなら、母集団における男女比が標本における男女比と異なっているので、標本から得たunweightedの集計値は、男性の回答の方向に偏ってしまうからです。
　もう少し経験のある方はこう答える。確かにウェイティングすべきでない場合もあります。この例では男女だけが問題になっていますが、男女、年代、地域、などなどと複数の層が登場すると、ウェイトを算出するためのサンプルサイズが小さくなり、極端なウェイトが得られてしまい、集計値はかえって不適切になってしまうことがあります。気をつけましょう。

　僭越ながら、この説明は間違っていると思う。少なくとも、ストーリーの半分しか語っていない。
　私はこう答えたい。ウェイティングすべきだとも、すべきでないともいえません。

シナリオA. ウェイティングすべき場合
　いくつかの架空のシナリオを考えよう。
　まず最初のシナリオ。私たちは知らないのだが、実は母集団における購入意向率は、男性で0.4, 女性で0.6であるとしよう(女性の評判のほうがよいわけだ)。関心があるのは全体の購入意向率だから、つまり0.5が「正解」である。
　このとき、標本における購入意向率は、男性で0.4のまわりの値、女性で0.6のまわりの値となる。標本は男性を多く含んでいるので、unweightedの集計値は男性の方向に向かって偏る。つまり、「正解」よりも少し低めになりやすい。
　下の図はその様子を示したものである。
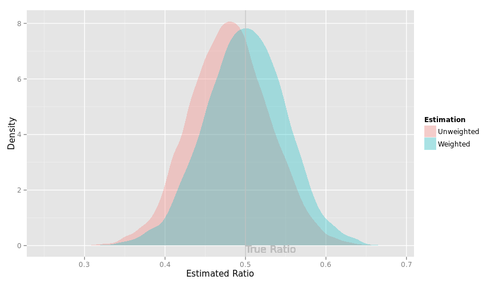
case 1 - distribution
赤の山は、この架空の調査をコンピュータ上で10000回繰り返し、unweightedの集計値がどのような値をとるかを調べた実験結果を示している(微妙にデコボコしているけど、あまり気にしないでください)。赤の山の位置は、「正解」よりも少し左側にずれている。
　いっぽう青の山はweightedの集計値の分布を示している。この山の真ん中(平均)は「正解」に一致する。つまり、ウェイティングによって、標本の男女比が母集団の男女比と異なることによる偏りを取り除くことができるわけである。
　よかった、よかった。これがウェイティングにとってハッピーなシナリオである。私たちはウェイティングすべきだ。

シナリオB. ウェイティングすべきでないシナリオ
　別のシナリオ。私たちは知らないのだが、実は母集団における購入意向率は、男性で0.5, 女性も0.5であるとしよう(購入意向は性別とは無関係なわけだ)。ここでも「正解」は0.5である。
　標本における購入意向率は、男性で0.5のまわりの値、女性で0.5のまわりの値となるだろう。標本は男性を多く含んでいるけれど、男女のあいだに差がないので、unweightedの集計値は偏らない。でもweightedの集計値も偏りはしない。だから「ウェイティングしてもしなくてもよい」。と考える人が多い。
　ここに落とし穴がある。このシナリオでの集計値の分布を示す。
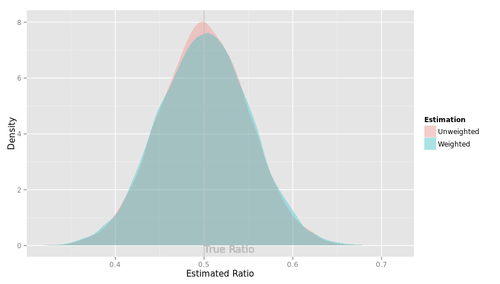
case 2 - distribution
確かに、赤の山も青の山も、「正解」である0.5のまわりに分布している。でもよく見ると、青の山のほうがほんの少し、下方向につぶれて、裾の広い形になっている。つまり、unweightedの集計値に比べてweightedの集計値は、「正解」からより離れた値をとりやすい。このシナリオでは、「ウェイティングしてもしなくてもよい」のではない。ウェイティングすべきでないのである。
　このように、weightedの集計値の分布は、unweightedの集計値の分布よりもばらつきが大きくなる。ウェイティングとは、集計値の分布のばらつきを犠牲にして、集計値の分布の偏りを取り除く手続きであるといえる。

シナリオC. 手に汗握るシナリオ
　シナリオAは、集計値の偏りをウェイティングによって取り除くのが望ましいシナリオであった。シナリオBは、集計値に偏りが存在せず、ウェイティングによって集計値がばらついてしまう害が顕在化するシナリオであった。
　では、その中間のシナリオ。母集団における購入意向率は性別によってわずかに異なり、男性で0.48, 女性は0.52であるとしよう。「正解」は0.5である。
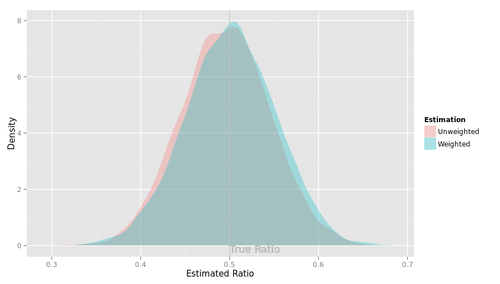
case 3 - distribution
unweightedの集計値の分布は少し左にずれている。いっぽうweightedの集計値の分布は、その平均が「正解」に一致している。その代償として、分布のばらつきは少し大きい。
　さて、どちらの集計値がよいだろうか？

　そもそも、私たちが求める集計値とはどんな集計値だろうか。
　weightedの集計値は、「正解」からみて偏りがない、すなわち、長い目で見て「正解」より大きくなりやすくも小さくなりやすくもない、という美点を持っている。いっぽうunweightedの集計値は、その分布の平均からみてばらつきが小さい、すなわち、長い目で見てその値が安定しているという美点を持っている。
　でも私たちは、長い目で見て性質の良い集計値を得るために調査を行っているのではない。たった1回の調査を通じて、母集団(潜在的顧客)の性質について少しでも正しい知識を得たいと思っているのである。だから本当に重要なのは、調査によって得られた集計値が「正解」により近いことである。
　上のシナリオで、集計値と「正解」0.5との差がどうなるかを計算してみよう。図でいえば、赤の山と青の山のそれぞれについて、山を形作る無数の点のそれぞれが、(その山の平均でなくて)「正解」0.5からどのくらい離れているかを調べてみる。統計学の伝統に従い、差を二乗した値を平均して表すことにする。これを平均二乗誤差という。
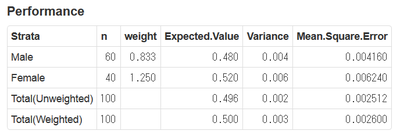
table3.png
unweightedの集計値の分布は、平均0.496(男性寄りに偏っている)。分散0.002。平均二乗誤差0.0025。
　weightedの集計値の分布は、平均0.5(偏りが取り除かれている)。分散0.003(すこし大きくなっている)。平均二乗誤差は0.0026。
　僅差ではあるが、unweightedのほうが誤差が小さい。つまり、このシナリオでは、私たちはウェイティングすべきでない。

シナリオのマップ
　これらの3つのシナリオでは、母集団の購入意向率が男女それぞれについてわかっていた。実際の調査は、母集団の性質がわからないからこそ行うわけだから、上のような図は手に入らない。
　しかし、こういう図を描くことはできる。
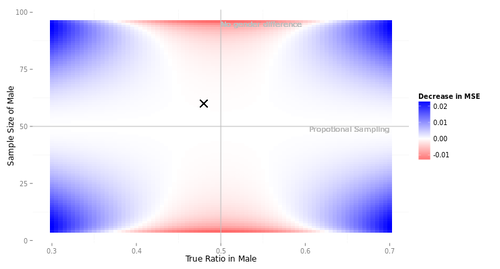
map3.png
この図は、母集団の男女比は5:5, 母集団全体での購入意向率は0.5, 標本サイズは100, という3点だけを決めて描いている。
　横軸は母集団における男性の購入意向率を示す。3つのシナリオでは、それぞれ横軸0.40, 0.50, 0.48であった。縦軸は男性の標本サイズを示す。3つのシナリオではすべて60であった。図中の×印はシナリオCを示している。
　図中の色は、unweightedの集計値の平均二乗誤差と、weightedの集計値の平均二乗誤差との差を表している。青のエリアは、ウェイティングした方が誤差が小さい(ウェイティングすべきである)。赤のエリアは、ウェイティングしないほうが誤差が小さい(ウェイティングすべきでない)。

　この図からいろいろなことがわかる。

「極端なウェイト」
　ウェイティングについての説明をみていると、ウェイティングの弊害として「ウェイトが極端なときは集計値の誤差が大きくなる」という点が挙げられていることが多い。この説明は当たっている面もある。上の図でいえば、ウェイト値は極端な値になるのは天井付近や床付近である。たしかに赤くなっている。
　しかし、赤のエリアは天井や床だけでなく、もっと内側にも広がっている。たとえば、さきほどの3つのシナリオはすべて、ウェイトは男0.833, 女1.250であった。これを「極端なウェイト」と呼ぶのは難しいだろう。それでも、ウェイティングによって誤差が大きくなる事態は生じた。
　このように、ウェイトが極端な値になるかどうかは、ウェイティングの是非にとって本質的問題ではない。

標本サイズとの関係　
　この図は状況によって変わる。全体の標本サイズを500に増やしてみよう。赤のエリアは小さくなってしまう。
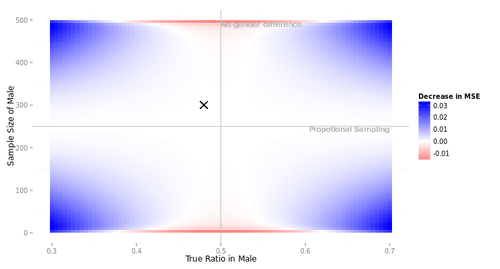
map4.png
このように、標本サイズが大きいとき、weightedの集計値はunweightedの集計値に比べて有利になる。
　これは次のように考えるとわかりやすいだろう。ウェイティングとは、集計値の偏りを取り除く代わりにばらつきを拡大する手続きである。集計値のばらつきは標本サイズと関係している。標本サイズが小さいときは、集計値のばらつきがもともと大きいので、ウェイティングによる拡大の影響が深刻でなる。それに対し、標本サイズが大きいときは、集計値のばらつきがもともと小さいので、ウェイティングによる拡大の影響はさほど問題にならない。
　このように、ウェイティングの是非を判断する際のひとつの重要なポイントは、全体の標本サイズである。

母集団特性との関係　
　もっと評判の悪い製品だったらどうなるか。標本サイズを100に戻し、今度は母集団全体の購入意向率を0.2に下げてみよう。
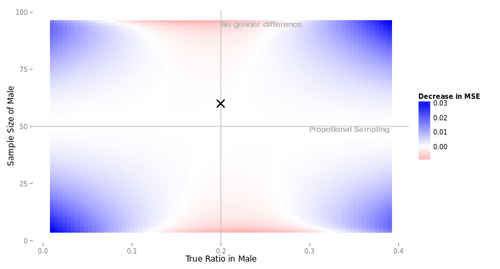
map5.png
興味深いことに、赤のエリアは左右非対称になる。よくみると、男性の標本サイズのほうが大きい場合(図の上半分)、男性のほうが購入意向が高い場合にはウェイティングすべきエリアが広く(図の右上)、男性のほうが購入意向が低い場合にはウェイティングすべきでないエリアが広い(図の左上)。
　これは割合という集計値の持っている性質に由来している。購入意向率とはすなわち購入意向者の割合である。割合という集計値は、真の値が0.5に近いときにばらつきが大きくなる性質を持っている。層別抽出においては、ばらつきが大きい層の標本サイズを増やしておけば、全体の集計値のばらつきを小さく押さえることができる。図の右上と左下がそれである。集計値のばらつきがもともと小さいぶん、ウェイティングにとって有利になる。

この実験からわかること　
　この簡単な実験から、次の点がわかる。ウェイティングすべきかどうかという問いに簡単な答えはない。
　標本抽出デザインだけからは、ウェイティングすべきだともすべきでないともいえない。たとえばこんな批判を耳にすることがある。「この調査、性別と年代で均等割り付けしている調査なのに、なんでウェイトバック集計していないんだ？」 こういう非難はいささか早計に過ぎると思う。非比例の層別抽出でも、あえてウェイティングしないという判断があってしかるべきである。ウェイティングは集計値の誤差を減らすこともあれば増やすこともあるのだ。

ではどうすればいいのか
　ウェイティングすべきかどうかという問いに簡単な答えはない。でも、あれこれ考えた上で、それなりの答えを出すことはできる。
　上の実験から、集計値の誤差という問題について考えるための簡単なガイドラインを手に入れることができる。その調査で測定した変数のうち重要な変数(たとえば購入意向)について、次の3点に注目すれば良い。

この3つの注意点に、冒頭に挙げた3つのポイント(適切なウェイトを構成できるか、能力とやる気があるか、分析の諸前提と整合するか)を加えれば、ウェイティングの是非を判断するための材料が揃うのではないかと思う。

シミュレータつくっちゃいました
　ところで、この文章を書いたもうひとつの理由、ささやかなほうの理由は...この文章で説明したシミュレーションを行うためのwebアプリを作ってしまったためである。図表はこのアプリでつくりました。
capture.png　URLは今後変わると思いますのでご注意ください。
　Shinyというシステムの使い方を勉強するつもりで作り始めて、たった半日でできてしまった。おそろしい時代になったものだ。
　ご関心あらばどなたでもお試しくださいまし。なかなか楽しいのではないかと思います。

2015/03/11 追記: アプリは停止しました。お粗末様でございました。

雑記：データ解析 - 「ウェイトバック集計」すべき場合とすべきでない場合がある(ということを説明するためのwebアプリを作ってしまった)

2014年3月26日 (水)

Hui, S.K., Huang, Y., Suher, J., Inman, J.J. (2013) Deconstructing the "First moment of truth": Understanding unplanned consideration and purchase conversion using in-store video tracking. Journal of Marketing Research. 50(4), 445-462.
　スーパーの買い物客にビデオカメラをつけるという研究。聞くだけで面白そうですね。

　本研究の関心は非計画購買にある。というわけで、まずは非計画購買についての先行研究概観。
　買い物前後の聴取に基づく研究：

　買い物の最中を追いかける研究 (おそらく全部著者らの仲間うちではないかと思うけど)：

　これらに対してこの研究は、購買の手前にある考慮のステップを捉えているのが新しい由。

　で、調査。実査は2009年。いやー、さすがだ。
　スーパーの入り口で来店客をリクルート。96個の製品カテゴリのリストを見せ(「野菜」から「練炭」まであるぞ)、買おうと思っている奴をチェックさせる。これが購買計画の有無になる。さらに、予算、買い物リストの有無、連れの有無、来店頻度 etc. を聴取。買い物リストを持ってる人は37%だそうだ。日本とはずいぶん違いますね。
　で、装置を着用させる。ヘッドセットみたいなのにカメラがついていて、対象者の視界が記録される。また、店舗内のRFIDタグをつかって位置が記録される。さらに、ロボコップみたいな格好になるので悪を倒せる。それは嘘ですけど。撮った動画の例がこちら。卵を買うとき、ちゃんとパックを空けて中をチェックするんですね。なかなか楽しい。まだ120viewしかないので、万一このブログをお読みの奇特な方がいらっしゃいましたら、ひとつ観てあげてください。
　買い物が終わったら出口調査。デモグラとか、衝動買い傾向尺度とか。店舗のご協力でレシートも集める。その日その日の店内ディスプレイももちろん記録してある。分析対象者は237人。すげえな。

　さあ、録りまくった動画をどうやって分析するか。人がいちいち観てコーディングするのである。大変だなあ。
　動画から「考慮」の期間を切り出す。基準は次の通り。次の３条件がそろったら「考慮」の開始とする。(1)あるカテゴリの棚に向かっている。(2)移動が止まるか、遅くなっている。(3)視界がそのカテゴリに固定されている。で、次のどちらかで「考慮」の終了とする。(1)移動の再開。(2)視界が別のカテゴリに移る。
　こうして切り出された考慮の回数は、0回から26回まで、平均13.1回。うち非計画考慮 (=入口調査でチェックしてなかったカテゴリについての考慮)は5.6回。

　お待ちかね、モデリングの時間です。別に待ってないけど。
　対象者を $i$, カテゴリを $j$, 購買計画有無を $s_{ij}$, 考慮有無を $r_{ij}$とする。以下、原文では記号に片っ端から右肩に$(r)$がついているんだけど(考慮のモデルであることを示している)、省略。
　まず、非計画考慮をモデル化する。非計画の状態 ($s_{ij}=0$) における「考慮することの潜在効用」$u_{ij}$ を考え、これが正だったら非計画考慮が生じると考える。この $u$ についてモデルを組む。説明変数は、個人特性、カテゴリ特性、カテゴリのプロモーション、カテゴリ間の相補性。
　$u_{ij} = \alpha + \tau_i + v_j + m_{ij} \varphi - \eta d_(j, s_i) + \epsilon_{ij}$
　$\epsilon_{ij} \sim N(0,1)$
　個人特性 $\tau_i$、つまり個人 $i$ の非計画考慮傾向は、デモグラ特性のベクトル $z_i$ で説明する。
　$\tau_i = z'_i \gamma + \zeta_i$
　$\zeta_i \sim N(0, \sigma^2_\zeta)$
　カテゴリ特性 $v_j$ は、カテゴリのhedonicity (別の研究からとってくる)、{要冷蔵/要冷凍/ほか}、の2要素からなるベクトル $c_j$ で説明する。
　$v_j = c'_j \Psi + \delta_j $
　$\delta_j \sim N(0, \sigma^2_\delta)$
書いてないけど、$m_{ij}$ は来店日のチラシ掲載有無であろう。
　最後に相補性。パスタの購買を計画している人はパスタ・ソースを非計画考慮しやすいだろう、という話である。カテゴリが散布する2次元空間を考え、カテゴリ $j, m$ 間のユークリッド距離 $dist(j,m)$ がカテゴリ間の相補性を表しているものとする。対象者 $i$ の購買計画ベクトル $s_i$ にはいっているすべてのカテゴリと、カテゴリ $j$ との距離の最小値を $d(j, s_i)$とする。
　以上を力づくで推定します！ もちろんMCMCで!!

　やれやれ。。。
　結果。チラシ掲載は非計画考慮にすごく効く。女性、高年齢者、予算に余裕がある人、買い物リストを持っていない人、店になじみがない人は非計画考慮しやすい。ヘドニックなカテゴリ、要冷凍のカテゴリでは非計画考慮が生じやすい。カテゴリ間相補性の空間も解釈容易(一番近いのは「カット済み野菜サラダ」と「米/豆/パスタ」だそうな)。

　では、計画考慮と非計画考慮はどうちがうのか。また、非計画考慮のうち購買につながったやつとつながらなかったやつはどうちがったか。
　それぞれの考慮について以下をコード化する。(1)時間: 滞在時間のなかのどのへんか。(2)場所: 店のどこにいるときか。(3)カテゴリ: ヘドニックである程度、要冷蔵、要冷凍。(4)関与。考慮の時間と、製品に触った回数(購買を除く)。(5)考慮の深さ。棚を見た回数と、棚と身体との距離。(6)外的情報へのアクセス。スタッフとのやりとり、ショッピングリストを見たか、店内表示を見たか。コーダーさんに深く同情いたします。
　結果。非計画考慮は、買い物の後半戦で生じやすく、購買につながる確率は低く(83% vs. 63%)、陳列棚(aisle)で起こりやすく、関与は浅く(製品接触回数が少ない)、考慮も浅く(棚との距離は長め)、外部情報へのアクセスは少ない。カテゴリがヘドニックかどうかは関係ない。
　非計画考慮のなかで購買につながる奴は、つながらない奴に比べ、陳列棚で生じやすく、ヘドニックなカテゴリで生じやすく、関与は深く考慮も深く外部情報アクセスが多い。

　というわけで、今度は非計画考慮のみを対象に、購買のモデルを組む。いやあ、すごい、肉食人種だ。
　新しい変数は次の2つ。(1)その時点での予算の残り金額。(2)その前の非計画考慮で購買したか。(3)考慮中の動画からコーディングした行動変数(関与、考慮の深さ、外部情報へのアクセス)。あとは同じ建付けのモデルである。
　結果。購買にチラシは効かない。店内ディスプレイは逆効果(非計画考慮の下での条件つき確率をモデル化しているので、筋は通っている)。陳列棚で生じやすい。デモグラ、カテゴリ特性はほぼ効かない。残り予算は効く。直前の非計画考慮で買っていると次の非計画考慮では買いにくい(なるほどね、これは面白いなあ)。などなど。
　相補性マップで一番近かったのは卵と調味料だったそうだ。こっちの相補性マップは、どう使えばいいのかピンとこないなあ。

　考察。今後の課題として、(1)調査協力者のバイアス。(2)入り口でカテゴリのリストを見せちゃっている点。(3)視界がわかるだけで見ているかどうかはわからない。(4)人力のコーディングは大変。(5)＜考慮→購買＞という図式が当てはまらないこともある。(6)非計画購買の動因として、ニーズを忘れていたのか、その場で発生したのかを区別すること。(7)別の業態。
　
　ううむ。この論文は非常に面白かった。データの充実、論旨の明確さ、展開の論理性、どこをとってもプロの研究者の論文である。このたび読んだ事情のほうの役には立たなかったんだけど、良いものを読んだ。
　アウトプットのなかで、非計画考慮の生起を説明するカテゴリ間相補性マップというのが一番面白いと思った。著者らも書いているけど、バスケット分析ではわからない、店内配置やクーポン発行への示唆が得られそうだ。

論文：マーケティング - 読了：Hui, Huang, Suher, & Inman (2013) 買物客の行動データで非計画購買を解剖する

　いわゆる「ウェイト・バック集計」、すなわち確率ウェイティングの下でデータ集計を行ったとき、ついでに平均や割合の差について検定をしようとすると、標準誤差はどうやって求めるのかという問題が生じる。確率ウェイトがごくシンプルなデザインに由来している場合は簡単で、たとえば層別一段抽出で層サイズが大きい場合であれば、層ごとに求めた標準誤差を合成すれば済むだろうと思うのだが、往々にして層は小さくウェイトは複雑である。テーラー展開か、リサンプリングか、はたまたロバスト推定か。ああ、嫌だ嫌だ、どうしたなら検定も信頼区間もない、静かな、静かな、データも何もぼうつとして物思ひのない處へ行かれるであらう (by 樋口一葉)。
　ところがある種のソフトウェアを見ていると、ややこしいことを考えないで、いわゆる有効ベース(この論文でいう等価標本サイズ)という考え方に基づき、あっさり検定統計量を修正してしまうものがある。ケースに付与されたウェイトの相対分散に応じて、標本サイズを一律に割り引いてしまうのである。わかりやすくていいけれど、でもそれってどうなの？ というのが、ずっと疑問であった。

Potthoff, R.F., Woodbury, M.A., Manton, K.G. (1992) "Equivalent sample size" and "Equivalent degrees of freedom" refinements for inference using survey weights under superpopulation models. Journal of American Statistical Association, 87(418), 383-396.
　というわけで、当該のソフトウェア(名前を挙げちゃうと、SPSS Data Collection)のマニュアルで引用されている論文。何年も前から積んであったのだけど、ここんところ確率ウェイティング関連の資料をめくっていたので、ついでに目を通しておくことにした。こういう話題は、いったん飽きたら本当に面倒になってしまうから。

　まず、概論。
　超母集団(母集団の母集団)という概念を導入する。この観点からいえば、確率的変動性(とでも訳せばいいのかしらん。stochasticity)にはふたつのソースがある。(1)超母集団の確率構造によって仮定されたもの。たとえば測定の変動性。(2)調査プロセスにおけるランダム化選択によって導入されたもの。つまり、仮に全数調査を行ったところで(1)は残り、推定量の分散は0にならないわけだ。
　サイズ $N$ の有限母集団からのサイズ $n$ の標本を考える。個体 $i$ のウェイトを $W_i$ とする。その由来は問わないけど、確率変数ではなく固定されていると考えることにする(そうしないとややこしくなるから)。合計を$W_{sum}$とする。
　いま、個体 $i$ の測定値 $y_i$ について
　$m_i = E( y_i ) $
　$v_i = var( y_i ) $
と考える。さらに、
　$m = (1 / W_{sum} ) \sum_i W_i m_i $
　$v = (1 / \sum_i W^2_i) \sum_i W^2_i v_i$
とする。$m$ の推定量
　$\hat{m} = (1/ W.) \sum_i W_i y_i $
について考えよう。その分散は
　$var(\hat{m}) = (\sum_i W^2_i / W^2_{sum}) v$
さて、上記4本の式を書き換える。まず、ウェイト値の合計の二乗をウェイト値の二乗の合計で割って
　$\hat{n} = W^2_{sum} / \sum_i W^2_i $
ウェイト値の合計をいったん1にし、これにこの値を掛けて、新しいウェイト値をつくる。
　$w_i = (\hat{n} / W_{sum}) W_i$
すると、4本の式はそれぞれ
　$m = (1 / \hat{n}) \sum_i w_i m_i$
　$v = (1 / \hat{n}) \sum_i w^2_i v_i$
　$\hat{m} = (1 / \hat{n}) \sum_i w_i y_i$
　$var(\hat{m}) = v / \hat{n}$
となる。このように、$\hat{n}$ は「等価標本サイズ」とでも呼ぶべきものになっている。なるほどねえ、鮮やかなものだ。

　$v$ の推定量としては
　$\hat{v} = 1 / (\hat{n} - 1) \sum_i w_i (y_i - \hat{m})$
を使えばいいんだけど、これが $v$ の不偏推定量になるのは、$v_i = v$ かつ $m_i = m$ のとき、つまり個体が等質なときである。そうでない場合、$E(\hat{v})$は $v$ より大き目、つまり保守的な推定量になる。
　信頼区間を求めたり検定したりする際には、自由度も修正しないといけない(ああ、そうか...)。どうやるのか延々説明してあるんだけど、面倒なので省略。そのほか、$v_i$ が変動している場合に $E(\hat{v})$ がとる範囲、$y_i$ が二値だった場合はどうなるか、などなど。省略。

　以下、各論。$v_i$ がなにか別の変数に比例していたらどうか。クラスタ抽出の場合はどうか。事後層別の場合のウェイト値の決め方。クラスタ抽出と事後層別の両方の場合はどうか。層別抽出の場合に限定したもっと良い方法。一元配置分散分析。$k \times 2$ 対応表での $k$ 群の等質性の検定。全部適当に読み飛ばしました。ごめんなさい、疲れました。

　というわけで、超母集団という概念に基づき、確率ウェイトつきデータを簡単に集計・分析するための「等価標本サイズ」「等価自由度」の求め方が示されているわけだが、細かい理屈はとても面倒そうなのであった。でもまあ、母集団分布についての一切の仮定抜き、というところは気分がいいですね。他の標準誤差推定と比べるとどうなのか、知りたいものだ。
　細かい話だけど、当該のソフトは標本サイズだけでなく自由度も修正してんのか、という点が気になった。マニュアルではどうもよくわからない。

論文：データ解析(-2014) - 読了：Potthoff, Woodbury, Manton (1992) 調査ウェイトつきデータの分析における「等価標本サイズ」「等価自由度」

2014年3月24日 (月)

　どうでもいい話だけど、今月は私の中でちょっとした「想像の共同体」ブームが起きていて(ほんとに面白い本だったのだ)、アンダーソンと関係しているものなら何でも読む！という状態だったのである。で、「いつかすごくヒマな時に読む資料」リストのなかにアンダーソンを引用しているのがみつかり、急遽昼飯のお伴に昇格させたのであった。

Muniz, A.M., O'Guinn, T.C. (2001) Brand Community. Journal of Consumer Research, 27(4), 412-432.
　ブランド・コミュニティと呼ぶべきものが存在しますよ、という論文。いまはやりの、企業がつくるブランド・コミュニティの話ではない。ブランド研究に新領域を切り開いた画期的な論文、らしい。
　アメリカの中産階級の４世帯を中心にしたエスノグラフィ。Ford Bronco, Macintosh, Saab の3ブランドについて、ブランドを中心にしたコミュニティと呼ぶべきものが生じている、ということを示す。コミュニティと呼ぶべきだという理由は、次の3つを満たしているから。

  1. ユーザの consciousness of kind. (いま調べたら「同類意識」と訳すらしい)。
  2. 儀式と伝統。Saab同士ならお互い手を振るとか、ブランド・ストーリーを共有しているとか、そういうの。
  3. moral responsibility。ユーザ同士助け合うとか。

　考察のところからいくつかメモ:

　前説と考察のあたりは気取った文章でうんざりしたけど、全体としてはとても面白い内容であった。最初は特殊なブランドの特殊な話だと思ったんだけど、なるほど、まあ確かにそういうのをコミュニティと呼んでもいいかもね、と説得されてしまった。新しい領域を切り開くというのはこういうことか。

　マーケティングという観点からはブランド視点で関心が持たれるところだと思うけれど、論文を読んでいて関心を引かれたのは、個人に視点をおいたとき、個々の消費者が参加するブランド・コミュニティはどういう組み合わせを持つだろうか、という点。コカ・コーラのコミュニティに参加する人はほかにどういうコミュニティに参加しやすいか。マクドナルド？ ひょっとして、サントリーだったりして...
　その手前の問題として、そもそもブランドのコミュニティという共同幻想に参加しやすい人と、そうでない人がいるのではないか、とも思う。早い話、私は事例記述を読んでいて、正直なところ非常にあほらしいと思ったのだが(すいません)、それは私の広い意味でのパーソナリティの問題かもしれないし、私がおかれた社会文化的状況が私にそういう余地を与えていない、ないし必要を与えていない、のかもしれない。

　それにしても、 消費を手がかりにしてはじめて饒舌に自分を語り、消費を手がかりにしてはじめて他人とつながることができる、そういう私たちの姿は、なにやら言い知れぬ哀しみを誘うなあ、と思うのだけれど... きっとこの論文の著者たちは、そもそも交換を含まないコミュニティなんてない、哀しんでないでこの新手の現象が持つ可能性に注目しろよ、と答えるんでしょうね。

論文：マーケティング - 読了：Muniz & O'Guinn (2001) ブランド・コミュニティ

2014年3月23日 (日)

　人々がどこかにお出かけしたり、おいしいものを食べたり、立派なことを言ったりしている間に、暗がりでジミーな論文をジトジトと読んでいるのでありました。魅力的な人物とは言いがたいね。

Patterson, B.H., Dayton, C.M., Graubard, B.I. (2002) Latent Class Analysis of Complex Sample Survey Data: Application to Dietary Data. Journal of the American Statistical Association, 97(459).
　えーと、複雑な標本デザインのデータについての潜在クラス分析(LCA)の方法を考えました、という論文。

　アメリカには全国レベルでの食生活調査がいくつかあって、たとえば何日かにわたって、過去24時間に野菜を食べた回数を聴取したりしている。そこで、潜在クラス分析によるデータ縮約を提案したい。ところがそういう調査は標本抽出デザインが複雑だ。というモチベーションがある由。著者らいわく、LCAに標本抽出デザインを組み込んだ報告はこれまでに見当たらないが(そうなんですか？)、回帰分析ではすでにある、とのこと。Korn & Graubard(1999, "Analysis of Health Surveys")というのが挙げられている。
　
　$J$ 項目の「食べた回数」設問への対象者 $i$ のベクトルを $Y_i$ とする。$j$ 番目の回答は 1から$R_j$までの離散値をとる。$L$個の潜在クラスを考え、$l$ 番目の潜在クラス $c_l$ のサイズを $\theta_l$ とし、そのメンバーが項目 $j$ に対して回答 $r$ を返す確率を $\alpha_{lkr}$とする。
　通常の潜在クラスモデル (LCM) であれば、
　$Pr(Y_i | c_l) = \prod_j \prod_r \alpha_{lkr}^{\delta_{ijr} }$
である($\delta_{ijr}$ は$y_{ij} = r$ のときに1, そうでないときに0)。対数尤度は
　$\Lambda = \sum_i ln \sum_l \theta_l Pr(Y_i | c_l) $
上の式を放り込んで
　$\Lambda = \sum_i \ln \{ \sum_l \theta_l \prod_j \prod_r \alpha_{lkr}^{\delta_{ijr}} \}$
シンプルだ。世の中の調査がみんな単純無作為抽出ならよかったのにね。
　さてここで、対象者 $i$ がウェイト $w_i$ を持っている。疑似対数尤度は
　$\Lambda = \sum_i w_i \ln \{ \sum_l \theta_l \prod_j \prod_r \alpha_{lkr}^{\delta_{ijr}} \}$
これを最大化する$\theta, \alpha$は母パラメータの一致推定量になることが示されている(Pfeffermann(1993) が挙げられている)。標準誤差の推定は難しくて(CSFIIのデザインにはクラスタも入っているので特に)、ごちゃごちゃ書いてあるけど、要するにジャックナイフ推定しますということなので、省略。実はそこんところが、この論文の売りらしいんだけど...どうもすいません。
　実データへの適用例。Continuing Survey of Food Intakes by Individuals (CSFII) という調査のデータを使う。多段の層別抽出で、ケースにウェイトがついている。野菜を食べた回数を4日分聴取している。食べた/食べないの二値に落として、weighted, unweightedそれぞれで2クラス解を推定。「野菜食べないクラス」のサイズが、unweightedよりweightedのほうで大幅に小さくなった。とかなんとか。そのほか、デザイン効果(deff)で標準誤差の見当をつけちゃだめだとか、Wald検定しましたとか、いろいろ説明してあるけど、スキップ。標準誤差のジャックナイフ推定の妥当性を示すためにシミュレーションしているけど、スキップ。どうもすいません。
　考察。ウェイティングすべきかせざるべきかという問題には長い歴史がある(以下を挙げている: Brewer & Mellor 1973; Smith 1976JRSS, 1984JRSS; Hansen, Madow, & Tepping 1983JASS; Fienberg 1989 in "Panel Surveys"; Kalton 1989 in "Panel Surveys"; Korn & Graubard 1995JRSS, 1995 Am.Stat.)。考慮すべき点は次の4つだろう:

  1. 目的は分析か記述か(←曖昧な言い方だと思うけど、どうやら共変量なしのLCMのような測定モデルを指して記述といっているらしい)。
  2. 要らないウェイティングをやっちゃったときのinefficiencyが、推定する効果に対して小さいか。
  3. ウェイティングしないときのバイアスの大きさ。
  4. 標本デザインについて十分な情報はあるか、また、ウェイティングせず標本デザインをモデル化するための変数が手に入るか。

　云々、云々。。。

　著者の先生方には大変申し訳ないんだけど、実はこの論文自体にはなんの関心もなくて、このあとのディスカッションが面白そうなので仕方なく読んだのである。この論文に対する４組の研究者によるコメントと、著者らによる返答がついている。主な論点をメモ。リングサイドよ、ゴングを鳴らせ！

　怖えーー！ Vermunt怖えーー！

　特に面白かった２つの指摘について詳しくメモしておく。まず、Elliott & Sammel のベイジアン・アプローチの話。

母平均の推測について考えよう。標本 $s$ が標本抽出デザインによって$H$個の層にわけられており、母集団における層のサイズはわかっているものとする。層 $h$ の位置パラメータ $\mu_h = E(y_{hi} | \mu_h)$ が、平均 $\mu$, 分散 $\tau^2$ の事前分布を持っていると考える。
　$\tau^2=\inf$ のとき、個々の $\mu_h$ は固定された独立な量で、層を通じた情報の共有はなく、母平均 $E(\bar{Y} | y \in s)$ の事後平均は、完全にウェイティングされた平均推定量 $\bar{y}_w = \sum_i w_i y_i / \sum_i w_i$ で与えられる。
　同様に、$\tau^2=0$ のとき、すべての $\mu_h$ は $\mu$ と同じことになり、$E(\bar{Y} | y)$ は全層をプールしたウェイティングされていない平均推定量で与えられる。
　$0 < \tau^2 < \inf$ とすれば、$E(\bar{Y} | y)$ の推定量は、不偏性と分散最小性の間のトレードオフを調整したものになり、平均平方誤差を小さくすることができる。このように、事前平均と分散に構造を与えることで、バイアスと分散のトレードオフを手元にあるデザインとデータ構造に対してチューニングすることができる(Elliott & Little, 2000)。
　このアプローチを拡張して、次の階層モデルを考える。二値の指標 $Y_{ij}$ について(※読みにくいので左辺を括弧でくくった)、
　$(Y_{hij} | c_l, \alpha_{hlj}) \sim BERNOULLI(\alpha_{hlj})$
　$(\alpha_{hlj} | c_l) \sim BETA(a_{lj}, b_{lj})$
　$(c_l | \theta_{hl}) \sim MULTINOMIAL(1, \theta_{hl}, L)$
　$(\theta_{hl}) \sim DIRICHLET(d_1, ..., d_L)$

云々。という風に、素知らぬ顔で階層ベイズモデルを持ち出す。なるほどね。でもちょっと面倒くさすぎる。。。

ふたつめ。Vermuntの原理的な批判。

　彼らが示した事例において、weightedの解がunweightedの解よりもより良いと云っていいものかどうか、私にはよくわからない。
　話を明確にするためには、潜在クラスモデルの2種類のパラメータを区別しておくことが大事だ。すなわち、潜在クラスの比率 $\theta_l$ と、項目の条件つき確率 $\alpha_{ijr}$ である。確かに、もし抽出ウェイトと相関する諸特性がクラスのメンバーシップとも相関していたら、$\theta_l$ のunweightedの推定値はバイアスを受ける。しかし注意すべきは、標準的な潜在クラス分析で得られた結果が妥当なのは、母集団が$\alpha_{ijr}$ について等質である場合に限られるという点である。仮にこの仮定が維持されているなら、$\alpha_{ijr}$ の推定の際に抽出ウェイトを使う必要はない。仮にこの仮定が維持されていないなら、抽出ウェイトを使っても問題は解決されない。$\alpha_{ijr}$ の異質性を、適切なグルーピング変数を導入した多群潜在クラス分析で取り扱わなけばならない。
　weightedの分析では標準誤差が大きくなる。だから私はunweightedの$\alpha_{ijr}$のほうがよいと思う。unweightの$\theta_l$はバイアスを受けるかもしれないが、それは$\alpha_{ijr}$をunweightedのML推定値に固定した上で、潜在クラス確率を(たとえば疑似ML推定で)再推定すれば修正できる。

　そうそうそう！ まさにそう思うんですよ！ 私が確率ウェイティングつきの多変量解析に対してふだん感じている違和感はまさにこれだ。ありがとうVermunt先生。やっと巡り会えたという感動でいっぱいです。

さて、著者らの返答。Vermuntの原理的批判に対する返答だけメモしておく。

　一般に、モデルが「正しく」指定されているかどうかを知ることは不可能だ。仮に可能であったとしても、その「正しい」モデルはむやみに複雑で解釈困難かもしれない。モデルが間違っている場合、Vermuntの2段階アプローチは「センサス」モデル(仮に母集団全体が標本になっていたら得られていたであろうモデル)を推定していない。
　これに対して、我々のweighted疑似尤度アプローチは、センサスモデルを推定している。このアプローチは、仮にモデルが間違っていても、異なる確率標本デザインからの推定値が平均してだいたい同じになるという利点を持っている。Vermuntの示唆する、まず等質な群を同定して項目の条件つき確率の異質性を取扱い次に多群潜在クラスモデルを用いるというやりかたは、現実性に欠け実行困難であるように思われる。

　うーん... そうかなあ...

　$\alpha_{ijr}$の異質性はないと信じる、というのはひとつの立派な考え方だと思う。異質性を正面からモデル化するというのも、実行可能性は別にして、もちろん立派な考え方だ。いっぽう、著者らの言い分はこうだ。「異質性があるかもしれないけど、まあそれは気にしないことにして、抽出デザインに起因するバイアスに対して頑健な推定値を求めましょう」。うーん、それってどうなんだろう...
　彼らのアプローチは結局のところ異質性を無視しているわけだ。そのことによってミスリーディングな結果を得てしまう危険性は、ウェイティングしようがしまいが変わらない。この話、とどのつまりは、(異質性がないという前提が正しい場合の)標準誤差を犠牲にして、(前提が間違っている場合の)抽出デザインに対する頑健性を得たいですか？ という問いに帰着するのではなかろうか。私の個人的な感覚としては、答えはNoだ...
　もっとも、彼らのいう「センサス・モデル」つまり「単純無作為標本の下で推定されていたであろうモデル」に、常になんらかの認識的価値が認められるのならば(実際には異質性が存在するのにそれを無視してしまっていた残念な場合においてさえ！)、そのときには彼らの手法には価値があるということになろう。かつてわたくしの元上司様は、「それが現象理解や意思決定の役に立つかどうかを別にして、手続き的に正しい結果を提出すればよい、あとのことは知らない」という市場調査会社の姿勢を指してシニカルに「コンナンデマシタケド」と呼んでいて、笑ってしまったのだが、私がいま想像できないだけで、そういう姿勢が求められる場面もあるかもしれない。うーむ。

　というわけで、「多変量解析での確率ウェイティングってなんなの？」というちょっとしたマイ・ブームのために、資料を手当たり次第にめくっていたのだけど、だんだん考え方が自分なりに整理できてきたような気がするので、そろそろ打ち止めにしておこう。

論文：データ解析(-2014) - 読了：Patterson, Dayton, Graubard (2002) 複雑な標本抽出デザインのデータに対する潜在クラス分析 (仁義なき質疑応答つき)

2014年3月21日 (金)

いわゆる「ウェイト・バック集計」関連の論文を集めてはパラパラめくる今日この頃である。ちょっと飽きてきた。

Asparouhov, T. (2005) Sampling weights in latent variable modeling. Structural Equation Modeling, 12(3), 411-434.
　著者はMuthen導師の弟子でMplus開発チームの人。確率ウェイティングを伴う潜在変数モデルの推定について、Mplusがお勧めする疑似最尤法(PML)、LISRELなどで用いられている重みつき最尤法(WML)、そして重みつき最小二乗法(WLS)を比較する、という内容。Mplusといってもversion 3だけど。
　主旨そのものは、ふうん... としかいいようがないんだけど、シミュレーションの部分が面白かったのでメモ。

　まず本題のほう。
　PMLもWMLも、重みつき対数尤度(ケースの対数尤度にケースのウェイトを掛けて合計したもの)を最大化するという点では変わらない。従ってパラメータ推定値は同一である。ちがうのは、推定量の共分散行列の推定方法である(なんだか超複雑な式がツラッと書いてあるけど、みなかったことにします)。よくわかんないけど、WMLというのは、まず重みつき標本統計量(平均と共分散)を求め、それに対してモデルを通常のML法でフィッティングするのと同じことなのだそうだ。本文の途中の説明では、「WMLというのは確率ウェイトをうっかり頻度ウェイトだと解釈したようなものだ」という記述もある。あー、なるほどね... これは目から鱗だ。
　WLSというのはカテゴリカル変数に対しても使える奴。まず切片や閾値や傾きについてのみ重みつき対数尤度を最大化し、推定値を固定して次に相関について重みつき対数尤度を最大化し... という面倒な手順を踏んでいる由。
　なおPMLとは、MplusでいうところのMLR推定量のことで、MLM, MLMVもこれに近い。WLSとはWLS, WLSM, WLSMV, ULSのこと。

　いくつかのシミュレーションを紹介。最後に、成長モデルについてMplus(MLR推定量), MLwiN, HLMを比較している。SASのproc mixedはHLMと同じらしい。うーん、他のソフトのことは知らないけど、SASのproc mixedのweight文は確率ウェイトを意味していないことがあきらかだから(いわゆるanalytic weight、測定値の誤差分散の逆数だと思う)、フェアな比較なのかどうかわからないけど... とにかくMplusの推定値が一番よかった由。とはいえ脚注によれば、LISRELやHLMではその後のバージョンアップによってもっと良い出力が出せるようになったそうだ。
　
　で、話をシミュレーションに戻すと... 一因子確認的因子分析(PML, WML)、潜在クラス分析(PML, WML)、カテゴリカル変数の一因子因子分析(WLS)、その「標本抽出がクラスタ抽出だったら」版(WLS), の4つについてシミュレーションする。まず適当な母集団モデルをつくって、つぎに標本抽出モデルをつくる、という手順。後者のモデルは、標本抽出の確率が指標によって決まるようなモデルである。どちらのモデルについても、パラメータをあれこれ動かしてみたりはしない、あっさりしたデモンストレーションなのだが、こんな選択バイアスがかかったら多変量解析の結果はどうなるでしょうか？ という頭の体操として、面白く読んだ。

　例題。連続変数5項目の一因子因子分析。真のモデルは、どの項目も負荷1, 切片0.3, 残差分散1, 因子分散0.8とする。で、ケースの抽出確率を1/(1+exp(-項目1))とする。項目1の値が高い人をオーバーサンプリングしているわけだ。ちなみにn=1000。さて、得られたデータをウェイティング抜きで因子分析する。項目1の負荷を1に固定して識別させる。さあ、推定結果はどうなるか？ 昼飯後のコーヒーショップでここまで読んで、あわてて頁を伏せ、目を閉じて考え始めたら、すこし居眠りしてしまった。
　正解。当然ながら、項目1の切片はやたらに高くなり(バイアスは+0.6)。残差分散はやたらに低くなる(-0.15)。他の項目も、切片はかなり高くなるが(+0.26くらい)、残差分散は影響されない。で、他の項目の因子負荷が高くなり(+0.16くらい)、因子分散は低くなる(-0.28)。なるほどー。

　というわけで、面白かったんだけど、いろいろ考えさせられる面もあった。
　潜在変数モデルにおける確率ウェイティングの出番、つまり「標本抽出確率の不均一性でバイアスが生まれており、確率ウェイティングでそのバイアスを除去できる」状況とは、いったいどんな状況だろうか。この論文では、「データの発生メカニズム自体に異質性はないけど、調査項目による標本選択が生じている」状況を想定しているわけだけど、現実の場面でそういうことは起きるだろうか。
　調査データの分析で単純な確率ウェイティングが用いられる二大場面は、非比例層別抽出、ならびに(たとえば調査無回答に対処するための)事後層別、だと思う。ふつう層別変数は対象者のデモグラフィック属性などで、調査項目や潜在変数からみると共変量だから、不均一な抽出による選択バイアスは、潜在変数の分布特性(たとえば因子分散)の推定には効いても、測定モデルのパラメータ(たとえば因子負荷)には効かないのではないかと思う。実際この論文でも、潜在クラス分析のシミュレーションのくだりで、抽出確率が(潜在クラスの指標となる項目ではなく)潜在クラスの予測子によって決まっている場合、選択バイアスは閾値の推定には効かない、と紹介している。もっとも閾値の分散の推定においては、ウェイティングを伴う正しい推定方式が必要になるわけだけど。
　層別変数が共変量ではなく、調査項目から見た結果変数になっている、というケースもあり得なくはない。たとえば、ある製品カテゴリに対する態度の調査で、ユーザと非ユーザに標本サイズを割りつけている場合がそれだ。でもこういう場合、そもそも各層の標本抽出確率がわからないので(潜在的消費者におけるユーザの割合がわからない)、ウェイティングしたくてもできない、ということが少なくない。それに、わざわざ指標と関連した層別を行っているからには、それらの層を通じた共通モデルという想定そのものが疑わしいことが多いと思う。ユーザと非ユーザでは態度の構造が違うだろう。

　そんなこんなで、因子分析や潜在クラス分析で確率ウェイティングをかけたい、どうしてもかけたい！という事態が、ちょっと想像しにくいように思うのだが、うーん、どうなんですかね。もっとも、これは私がパラメータ推定にばかり目を向けているからで、パラメータの信頼区間やモデルのカイ二乗値に強い関心があれば、話は少し変わってくるだろう。

論文：データ解析(-2014) - 読了：Asparouhov(2005) 因子分析・潜在クラス分析における確率ウェイティング(または: Mplus 3はこんなにすごいんだぜ)

2014年3月18日 (火)

Bookcover 定本 想像の共同体―ナショナリズムの起源と流行 (社会科学の冒険 2-4) [a]
ベネディクト・アンダーソン / 書籍工房早山 / 2007-07-31
　よく考えてみると読んでなかった敷居の高い本に思い切ってチャレンジする「実をいうと読んでなかった」シリーズ、M.ウェーバー、I.ハッキングに続く第三弾。なんだか有名な本だという知識だけが先行してしまい、どうも手に取りづらかった。
　ところがどっこい、思い切って読み始めたら、これが稀にみる面白本で... 1991年刊の増補版で読んでいたのを中断し、わざわざ2006年刊の新版を買い直して読んだ。

　題名から受ける印象に反し、単に「国民国家というのは想像された共同体なのですよ」という本ではない。その想像の共同体がいかにして成立したか、その複雑なプロセスを丁寧に説き明かす本なのであった。
　一度手に取ったら止められない、実にエキサイティングな内容で、読み終えてからもしばらくは心のなかでブームが続き、適当な箇所を開いて読み返しては面白がっていたのであった。ここんところの一大ヒット。

Bookcover 禁欲のヨーロッパ - 修道院の起源 (中公新書) [a]
佐藤 彰一 / 中央公論新社 / 2014-02-24

Bookcover ローマ五賢帝 「輝ける世紀」の虚像と実像 (講談社学術文庫) [a]
南川 高志 / 講談社 / 2014-01-11

Bookcover チャーチル―イギリス現代史を転換させた一人の政治家　増補版　 (中公新書) [a]
河合 秀和 / 中央公論社 / 1998-01-25
見方によっては偉大な人であろうが、民主主義的な政治家とは言いがたい...

Bookcover トクヴィルが見たアメリカ: 現代デモクラシーの誕生 [a]
レオ ダムロッシュ / 白水社 / 2012-11-23
「アメリカのデモクラシー」を読む前の景気づけに、と思って手に取った本。トクヴィルのアメリカ旅行を追跡する面白い内容であったが、やはりトクヴィル自身の本を読まないと、価値も半減であろう。

ノンフィクション(2011-) - 読了：「想像の共同体」「トクヴィルが見たアメリカ」「ローマ五賢帝」「禁欲のヨーロッパ」「チャーチル」

Bookcover 無念なり: 近衛文麿の闘い [a]
大野 芳 / 平凡社 / 2014-01-24
近衛は決して優柔不断な政治家ではなかった。木戸幸一と都留重人の陰謀が彼を追い詰めた。など、工藤美代子「われ巣鴨に出頭せず」に近い内容であった。

日本近現代史 - 読了：「無念なり　近衛文麿の闘い」

Bookcover 百姓貴族 (3) (ウィングス・コミックス) [a]
荒川 弘 / 新書館 / 2014-02-25

Bookcover エイス(3)<完> (モーニング KC) [a]
伊図 透 / 講談社 / 2014-02-21
デビュー作「ミツバチのキス」と同じく、せっかく広げた魅力的な風呂敷をきちんと畳まないまま終わってしまうのではないかと勝手に心配していたのだが、やっぱりそういう風になってしまった... ちょっと残念だなあ。

Bookcover 銀の匙 Silver Spoon 11 (少年サンデーコミックス) [a]
荒川 弘 / 小学館 / 2014-03-05

Bookcover 闇金ウシジマくん 30 (ビッグコミックス) [a]
真鍋 昌平 / 小学館 / 2014-02-28

Bookcover 甘々と稲妻(2) (アフタヌーンKC) [a]
雨隠 ギド / 講談社 / 2014-03-07
暴力的にお腹が空いてくる。このマンガが嫌いだという人は少ないだろう。

Bookcover 千年万年りんごの子(3)<完> (KCx(ITAN)) [a]
田中 相 / 講談社 / 2014-03-07

コミックス(2011-) - 読了：「百姓貴族」「エイス」「銀の匙」「闇金ウシジマくん」「甘々と稲妻」「千年万年りんごの子」

読了の本が溜まってしまったので、とりあえずコミックスについて記録しておく。

Bookcover 繕い裁つ人(5) (KCデラックス Kiss) [a]
池辺 葵 / 講談社 / 2014-03-13
地味なマンガなんだけど、どんどん良くなってくるなあ。映画化するそうだ。

Bookcover めめんと森 (フィールコミックス) (Feelコミックス) [a]
ふみふみこ / 祥伝社 / 2013-12-07
死と向かい合う女を描いたシリアスなストーリーなんだけど、それよか、こういう虫も殺さないような女の子がいきなり男と寝ちゃうと。。。ヤラシイですねえ。

Bookcover シュトヘル 9 (BIG SPIRITS COMICS SPECIAL) [a]
伊藤 悠 / 小学館 / 2014-02-28

Bookcover 蜜の島(2) (モーニング KC) [a]
小池 ノクト / 講談社 / 2014-02-21

Bookcover アイアムアヒーロー 14 (ビッグコミックス) [a]
花沢 健吾 / 小学館 / 2014-02-28
ゾンビ・パニックものの傑作。まさか、ゾンビたちに追い詰められながら、箱根湯本のかっぱ天国でお湯に浸かる事になるとは...

Bookcover 34歳無職さん 4 (MFコミックス フラッパーシリーズ) [a]
いけだたかし / KADOKAWA/メディアファクトリー / 2014-02-22

コミックス(2011-) - 読了：「繕い裁つ人」「めめんと森」「シュトヘル」「蜜の島」「アイアムアヒーロー」「34歳無職さん」

Pearl (2014) Understanding Simpson's Paradox. The American Statistician, 68(1), 8-13.
　因果推論の巨匠Pearl先生、シンプソン・パラドクスについて語るの巻。
　シンプソン・パラドクスとはすなわち、二元クロス表における連関が、第三の変数で層別すると消えたり方向が逆になったりする... という話。統計や調査法の本によく登場する有名な現象である。こう表現してしまうとつまらなく聞こえるけど、はじめて実物をみたら、それはもうビビりますよ。講義やセミナーなどでみせると、何人かは身を乗り出して食いついて下さる、良い題材である。

　Pearl先生いわく:
　あるパラドクスが解けていると主張するためには、以下の基準をクリアしなければならない。(1)その現象が驚きをもたらす理由を説明できること。(2)パラドクスが現れるシナリオと現れないシナリオを区別できること。(3)それが現れるシナリオにおける意思決定の正解を示し、数学的に証明すること。
　この基準に照らせば、シンプソン・パラドクスはもう「解けている」。順に示しましょう。

　(1)について。シンプソンのパラドクスがパラドクスとみなされるのは、その現象が私たちが抱いている次の因果的信念と衝突するからだ: 「それぞれの下位母集団において事象Bの確率を増大させる行為Aは、それが下位母集団の分布を変えない限り、母集団全体においてもBの確率を増大させるはずだ」。著書"Causality"ではこれを"sure-thing"の定理と呼んでいる。つまり、シンプソンのパラドクスの驚きは、統計的連関に因果的解釈を与えてしまうという私たちの傾向性と、私たちの因果的直観に起因している。
　(2)について。シナリオは有向非循環グラフ(DAG)によって表現できる。シンプソン・パラドクスが起きるシナリオとそうでないシナリオもDAGで区別できる。
　(3)について。伝家の宝刀do-calculusで説明できる。しかしdo-calculusをご存じない読者の皆様のために(←今日はやけに親切ですね先生)、ここではシミュレーションによって説明しよう... というわけで、バックドア基準のかんたんなご紹介。

　Pearl先生のこういう非専門家向けの文章は、読みやすくて面白い。この論文も、出先での時間待ちのあいだに楽しく読んだ。なのに、主著"Causality"ときたら、なぜあんなにわかりにくいんですかね...

　この論文、いちおうはArmistedという人の批判論文への返答という形をとっているのだけれど、本文中では全く言及がなく、最後に短くコメントしているのみ。いわく：はいはい、あなたの云っていることは正しいでしょうよ。XとYのクロス表をZで層別しようがしまいがお好きなように。どんな集計表だってなにかの役には立つでしょう。でも、Yに対するXの総合効果に関心があるならば、みるべき表は、Zで層別した表かしない表のどちらか一方に決まります。という、言い回しは優しいけど、ほとんど相手にしていない感じの返答であった。そりゃそうですよね先生！ Armistedの批判が批判になっているのかどうか理解できず不安だったのだけど、ひと安心。虎の威を借る狐とはこのことである。

論文：データ解析(-2014) - 読了：Pearl (2014) シンプソン・パラドクスよ、お前はもう解けている

2015/06/10 追記: 一年以上前に書いたこの記事を自分で読み返していたら、シミュレーションのコードは汚いわ、結果を読み違えているわで、いやあ、こっぱずかしい... 以下、書き直しました。

Spencer, D. (2000) An approximate design effect for unequal weighting when measurements may correlate with selection probabilities.　Survey Methodology, 26(2), 137-138.
　最近読んだ何本かの論文で引用されていたので、ついでに目を通した。

　抽出確率が不均一な調査デザインのデータにおいては、バイアスを取り除くために集計の際に確率ウェイティングを行うことがあるが、その副作用として母集団パラメータの推定精度が低下する。この推定精度の低下を、推定量の分散と「単純無作為抽出の場合における推定量の分散」との比で表してデザイン効果と呼ぶ。
　Kishの有名な近似式によれば、母平均推測における層別抽出のデザイン効果は、ウェイト値の相対分散を$rvw$として$1+rvw$である。しかし、Kishの近似式は抽出確率と無関連な変数の集計を想定している。抽出確率と関連している変数については、推定精度はむしろ向上する場合さえある。そういう場合の近似式をご提案します、という短い報告。

　母集団サイズを$N$とする。ケースをひとつ抽出したときそれがケース$i$である確率を$P_i$とする。当然、母集団を通した$P_i$の平均は$1/N$になる。ケース$i$の測定値を$y_i$とする。
　いま、母集団において回帰式
　$y_i = \alpha + \beta P_i + \epsilon_i$
　が成り立っているとしよう。
　以下、母分散を$\sigma^2$, 母相関を$\rho$で表す。原文ではそのあとに添え字がついているけど($\sigma^2_y$とか)、わかりにくいのでかっこに入れて示す($\sigma^2[y]$とする)。
　サンプルサイズ$n$の標本について考える。以下ではウェイトを、(抽出確率)*(標本サイズ)の逆数、すなわち$w_i = 1/(n P_i)$と表現する。

　母集団合計$Y$の推定について考える。推定量は
　$\hat{Y} = \sum^n_i w_i y_i$
その分散は
　$V(\hat{Y}) = (1/n) \sum^N_i P_i (y_i / P_i - Y)^2$
ここにさっきの回帰式を放り込むと下式となる由。母集団を通じた$w_i$の平均を$\bar{W}$として、
　$V(\hat{y})$
　$= \alpha^2 N(\bar{W}-N/n)$
　$+ (1-\rho^2[y, P]) \sigma^2[y] N \bar{W}$
　$+ N \rho[\epsilon^2, w] \sigma[\epsilon^2] \sigma[w]$
　$+ 2 \alpha N \rho[\epsilon, w] \sigma[\epsilon] \sigma[w]$
導出過程を追いかけてないけど、信じますよ、先生。

　さて、さきほどの回帰式が測定値$y_i$と抽出確率$P_i$ の関係をうまく捉えているならば、それがどんな関係であろうが(関係があろうがなかろうが)、残差項とウェイトは無相関である。すると、上式の$\rho[\epsilon^2, w], \rho_[\epsilon, w]$が$0$になるから、
　$V(\hat{y}) = \alpha^2 N(\bar{W}-N/n) + (1-\rho^2[y, P]) \sigma^2[y] N \bar{W}$
いっぽう、単純無作為抽出の場合の分散は (話を簡単にするために復元抽出だとして)
　$V(\hat{y}) = (1/n) N^2 \sigma^2[y]$
この比をとったのがデザイン効果だ。すなわち
　$deff = (\alpha/\sigma[y])^2 (n \bar{W} / N - 1) + (1-\rho^2[y, P]) n \bar{W} / N$
このデザイン効果の推定値は、結局
　$(\hat\alpha/\hat\sigma[y])^2 (rvw) + (1-\hat\rho^2[y, P]) (1+rvw)$
となる由。Kishが想定した$y$と$P$が無相関な状況では、$\hat\alpha$も$0$に近くなるから、結局
　$1 + rvw$
となるわけで、つじつまが合っている。
　...という主旨の論文であった。

　へー、そうなの？と思って、ちょっと実験してみた。

　母集団が5つの層から構成されていると考える。層の構成比は1:2:3:4:5とする。各層の母平均をいろいろ操作し、次の3つを比較した。

サンプルサイズは100。測定値は(母平均)+(SD1の正規ノイズ)として生成した。試行数5万のモンテカルロ・シミュレーション。シミュレーションのRコードはこちらにございます。コーディングが下手なのはお慰みで。

　結果はこうなりました。クリックで拡大表示されるはず。

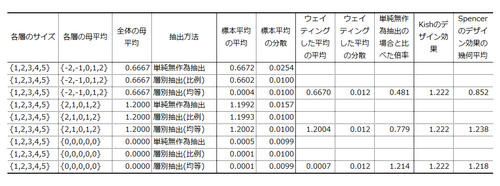
table.png

　シナリオ1. Spencerのデザイン効果の活躍が期待される状況。各層の母平均を{-2,-1,0,+1,+2}とし、全体の母平均(0.6667)を推測した。単純無作為抽出による標本平均は分散0.0254。これに対し、層別抽出(比例)による標本平均は分散0.0100。層別抽出(均等)による母平均の推定値(つまりウェイティングした平均)は分散0.0122。単純無作為抽出に比べて分散が0.481倍に激減している。層が測定値と抽出確率の両方と強く関連しているので、層別抽出が猛烈な威力を発揮したわけだ。
　層別抽出の毎試行ごとにSpencerのデザイン効果を算出してみると、その幾何平均は0.852であった。Kishのデザイン効果(1.222)は推定量の分散の減少を捉えることができないが、Spencerのデザイン効果も減少の大きさを捉えきれていない。なぜだろう？

　シナリオ2. Spencerくんの手にも負えないであろう状況。各層の母平均を{+2,+1,0,+1,+2}としてみる(全体の母平均は1.2)。単純無作為抽出では、標本平均の分散は0.0157。層別抽出(比例)では分散0.0100。層別抽出(均等)では分散0.0122。単純無作為抽出に比べて分散が0.779倍に減少している。さきほどと同様、層別抽出にしておいてよかった、というケースである。
　Spencerのデザイン効果の幾何平均は1.2380。Kishのデザイン効果はもちろんSpencerのデザイン効果も、標準誤差の減少を捉えられない。測定値と抽出確率のあいだに強い関係があるのだが、それが非線形であるためだろう。

　シナリオ3. Kish先生のやり方でよさそうな状況。各層の母平均を{0,0,0,0,0}としてみた(全体の母平均はもちろん0)。単純無作為抽出では、標本平均の平均は分散は0.0099。層別抽出(比例)では分散0.0100。層別抽出(均等)では分散0.0120。要りもしないウェイティングをしたせいで、標準誤差が1.214倍に拡大してしまったわけだ。
　Spencerのデザイン効果の幾何平均は1.218であった。この状況なら、Kishのデザイン効果(1.222)もSpencerのデザイン効果も、まあまああたっている。

　うーむ。シナリオ 1 における推定量の分散の減少を捉えきれないとすると、Spencerの近似式が役に立つのは一体どういうときなのか、いまいちわからなくなってきた。

論文：データ解析(-2014) - 読了：Spencer(2000) 抽出確率が測定値と相関している標本におけるデザイン効果の推測

2014年3月12日 (水)

　またもや「ウェイトバック集計」関連の論文。非比例層別抽出のような、個体のあいだで標本抽出確率が均一でない標本があるとき、確率ウェイティングの下での集計・検定を行うことは多いけど、では回帰分析や因子分析も「ウェイトバック」すべきか。これは大変難しい問題で、いつも答えに困る。厄介なことに、最近はソフトウェアが進歩して、単に「できません」と答えるわけにもいかなくなっている...

Muthen, B., & Satorra, A. (1995) Complex sample data in structural equation modeling. Sociological Methodology, 25, 267-316.
　確率ウェイトつきの調査データに対する多変量解析についての概観が読みたくてめくった。掲載誌は年報のような感じ。
　いやはや、長くて難しい内容であった。困るなあベン、もっと易しく書いてくれないとさあ。(←論文を何本も読んだのでもはやマブダチである。俺の中ではな)

　まず、先行研究概観。complex sample design のデータ解析手法は2つに分けられる。

　別の観点からは次の2つに分けられる。

先日読んだGelmanさんも云ってたけど、いわゆるモデル・ベースのアプローチだって標本抽出デザインについての情報を使っているのだから、なんだか変な区別なんですけどね。まあこの業界の常識的区別なのであろう。以上の区別については、Skinner, Holt, Smith, eds.(1989) "Analysis of Complex Surveys"を参照せよとのこと。

　で、先行研究を、単変量のデザイン・ベース、単変量のモデル・ベース、多変量、の3節に分けて紹介。

　以上はこの論文のほんの序盤で、ここからが本題。まず、SEMを一般的に定式化し、complex sampleに対するaggregatedのモデルとdisaggregatedのモデルを定式化する。それも正規性がある場合とない場合の両方について。正直いって私の能力の及ぶところではないので、パス。
　で、モンテカルロ・シミュレーション。層やクラスタが出てくるややこしい標本抽出デザインのデータに対する回帰分析と因子分析について、(1)正規性を仮定したML推定(SRSを想定)、(2)robust normal theory に基づく推定(すなわちデザイン・ベース)、(3)マルチレベルモデル(すなわちモデル・ベース)の3つの性能を比較。(2)(3)の性能がいいね、云々。根気が尽きたのでパス。

　というわけで、大部分はパラパラとめくっただけだけど、目的は達したので、読了ということにしておいてやろう。なんだかあれだな、散々殴られた挙句に「今日はこのくらいにしておいてやるか」と言い捨てて立ち去るチンピラみたいだな。

論文：データ解析(-2014) - 読了：Muthen & Satorra (1995) 複雑な標本抽出デザインのデータに対するSEM

2014年3月11日 (火)

　ひょんなことから、いわゆるウェイト・バック集計について考える機会があった(年に何回かそういうことがある)。ふと思いついて、日本語での解説をwebで探してみたら、みつかるページはピンキリである。大変失礼ながら、かなりイイカゲンな説明が多い。「ウェイトバック後のサンプル数」とか。それはいったいなんだ。
　OJTというのはあてにならないもので、いま関わっている市場調査の分野を見ていると、経験を積んだ優秀なリサーチャーの方でも、この話に関しては結構怪しげな考え方をすることがある。性別や年齢のような共変量について、母集団の構成比率と標本の構成比率とを事後層別ウェイティングで揃えることは、それが可能な限りにおいて常に善である、とか。そんなことはない。一般に確率ウェイティングは推定量の分散を増大させる。個別の調査データ解析にとってホントに大事なのは不偏推定ではなく推定誤差の最小化なのだ。デザイン効果やeffective sample sizeって聞いたことないんですかね？ ... と思ったところで、ハタと気が付いた。ごめんなさい、私もいまいちよくわかってないです。お世辞にも得意分野とはいえない。

Park, I. & Lee, H. (2001) The design effect : Do we know all about it? Proceedings of the Annual Meeting of the American Statistical Association. 2001.
　というわけで反省して、昼飯のついでにいくつかの資料に目を通した、そのなかの一本。ASAのProceedingsだけど、タイトルがそのものずばりだったので。著者らはWestat社の人。

　まず、デザイン効果の小史。

　さて。母集団パラメータとして合計 $Y$ と 平均 $\bar{Y}$ に注目しよう。複雑な抽出デザインにおいて、合計の不偏推定量は $\hat{Y} = \sum w_i y_i$ (w_iはどなたかが宜しく作ってくれたとして)、平均の不偏推定量は $\hat{\bar{Y}} = \sum w_i y_i / \sum w_i$ である。良く似ている。しかし、$Deft(p, \hat{Y})$ と $Deft(p, \hat{\bar{Y}})$ は全然違っている。前者のDeftはとても大きい。
　Kish(1995)はこういっている。「Deftは要素の変動性($S^2_y / n$)のむこうにある標本デザインの効果を表現するために用いられる。そのために、測定単位と標本サイズの両方を剰余変数として除外するのである。測定単位 $S_y$ とサンプルサイズ $n$ を取り除くことで、標本誤差におけるデザインの効果が他の統計量や他の変数に一般化できるようになる。同じ調査のなかでも、異なる調査の間でさえ」。この言葉は $\hat{\bar{Y}}$ についてはだいたい正しいが、$\hat{Y}$ については正しくない。

　というわけで、この論文の本題は、合計に対するdesign effectの話であった。そうタイトルに書いといてほしいなあ。
　有限母集団 $U$ からの、ある複雑なデザインによる標本サイズ $n$ の復元抽出を考えよう。要素 $k$ の値を $y_k$ とする。$k$ の抽出確率を $p_k$ とし、$U$ を通じて $\sum p_k = 1$ と基準化する。$i$ 番目に抽出された単位を $k_i$ とする。$y_{k_i}$ とか書くのが面倒なので $y_i$ と書く。
　母合計 $Y = \sum y_k$ の推定量は
　$\hat{Y} = 1/n \sum_i y_i / p_i$
これをHansen-Hurwitz推定量という(へー。知らなかった)。その分散は、
　$Var(\hat{Y}) = 1/n \sum_U (1/p_i) (y_i - p_i Y)^2$
いっぽう、母平均 $\bar{Y} = Y / N$ の推定量は、
　$\hat{\bar{Y}} = \hat{Y} / \hat{N}$
ただし、$\hat{N} = \sum_i (1/np_i)$ である。
式の展開は端折って、それぞれのDeftは以下のようになる由。$N$ が十分大きいとして、
　$Deft^2 (\hat{Y}) \approx { \sum_U (1/p_i) (y_i - p_i Y)^2 } / {\sum_U N (y_i - \bar{Y})^2 }$
　$Deft^2 (\hat{\bar{Y}}) \approx { \sum_U (1/p_i) (y_i - \bar{Y})^2 } / {\sum_U N (y_i - \bar{Y})^2 }$
ここで $p_i$ と $y_i$ の無相関を仮定すると、二本目の式はKishの与えた有名な近似式 1 + ($w_i$の相対分散) に帰着する。
　さて、上の二本の式を整理すると、結局
　$Deft^2 (\hat{Y}) - Deft^2 (\hat{\bar{Y}}) = (1/CV_y^2) {\sum_U (1/p_i) (p_i - \bar{P})^2 - (2/Y) \sum_U (1/p_i) (y_i - \bar{Y})(p_i - \bar{P}) }$
ただし $CV_y = S_y / \bar{Y}$。つまり、合計に対するデザイン効果は、平均に対するデザイン効果よりも大きくなる。その増分は、$y$ の分散が小さいとき、$p_i$ の分散が大きいとき、$p_i$ と $y_i$ の相関がないとき、に大きくなる。へえー。

　最後に、Spencer(2000)による修正式が合計に対しては当てはまらない、という説明。それからデータ例。読み飛ばした。
　結論。合計の推定におけるデザイン効果はKishの説明とは異なり、変数の分散や変数と抽出確率との相関に依存するから注意しないといけない。云々。

　ある複雑なデザインの調査データを集計する際に、確率ウェイティングを行うかどうか悩む場合がある。その判断の手がかりになるのが、確率ウェイティングによる推定精度の低下の評価、すなわちデザイン効果の推定である。いっぽう集計の際には、確率ウェイティングだけでなく、頻度について母集団サイズへの拡大推計を行うこともある。この2つは全然別の事柄だから、まず確率ウェイティングの是非について考え、ウェイティングするかどうか決め、割合を求め、それに母集団サイズを掛ければいいや、と思っていた。でもこの論文によれば、母集団における頻度を統計量と捉えたとき、その推定量におけるデザイン効果は平均のデザイン効果より大きくなるわけだ。ということは、拡大推計を行う際はそのことを考慮して、ウェイティングの是非をよりシビアに判断する必要がある、ということになりそうだ。うううむ。そうなのか。あとでよく考えてみよう。とにかく、意外な面で勉強になりました。

　ところで、この文章によれば、KishがDeftを提案したのは1992年の論文"Weighting for Unequal P_i"である。この論文はかなり前に読んだのだけど、デザイン効果についての突っ込んだ議論はなかったし、記憶が正しければそもそもDeftなんて出てこなかったように思う。著者らはなにかと勘違いしているのではないだろうか。調べてみると、1995年の"Methods for Design Effects"という論文が怪しい。掲載誌はどちらもJ. Official Statisticsだし。

論文：データ解析(-2014) - 読了: Park & Lee (2001) デザイン効果、その知られざる真実

2014年3月 7日 (金)

因果推論の巨匠 J. Pearl 先生が「こんどこんな論文書いたから読んでね」と下書きを公開する→たまたま気づいて、いつか読もうと印刷して机に積む→しばらく放置→整理の都合でぱらぱらとめくったら、これが面白そう→いや待て、修正が済んだやつがもう雑誌に載っているんじゃないかと探す→American Statisticianの最新号に載っていて、前後の論文含めPDFが無料公開されていることに気づく→あろうことか下書きとは主旨が変わって、誰かのPearl批判論文への返答という位置づけになっている→仕方がないのでその批判論文を読み始める→さっぱり理解できず困惑する(イマココ)

Armisted, T.W. (2014) Resurrecting the Third Variable: A critiquie of Pearl's causal analysis of Simpson's paradox. American Statistician, 68(1), 1-7.
　というわけで、この雑誌の最新号に載っているシンプソン・パラドクスについてのやりとりの、最初の論文。
　ええと...　因果推論の巨匠 Pearl 先生に言わせれば(著書"Causality")、シンプソン・パラドクスはパラドクスではない。因果性の問題として考えるべき問題を、そう考えそこねていることに由来する混乱に過ぎない。いっぽう著者はこの考え方を批判する。どう批判するかというと、ええと、ええと...
　
　まずはこんな例から。Lindley&Novick(1981) というのが挙げた例だそうだ。

全体:
治療あり... 治癒20名, 非治癒20名, 治癒率50%
治療なし... 治癒16名, 非治癒24名, 治癒率40%
男性:
治療あり... 治癒18名, 非治癒12名, 治癒率60%
治療なし... 治癒7名, 非治癒3名, 治癒率70%
女性:
治療あり... 治癒2名, 非治癒8名, 治癒率20%
治療なし... 治癒9名, 非治癒21名, 治癒率30%

全体をみると治療ありのほうが治癒率が高い。しかし性で層別すると、どちらの層でも治療なしのほうが治癒率が高い。シンプソン・パラドクスである。
　Pearlの説明はこうだ。この例で、全体の表は性別情報がないときの治療の「証拠の重み」を示しているに過ぎない。治療の効果を示しているのは層別した表である。いっぽう、「男性」「女性」を「低血圧も治った」「低血圧は治ってない」に書き換えた場合はどうか。その場合は全体の表のほうをみないといけない。なぜなら低血圧が治ったかどうかは治療の結果だからだ。つまり、性というcausalな変数では層別すべきだが、低血圧が治ったかというnoncausalな変数では層別してはいけない。
　いっぽうLindleyらの説明は少しちがう。この例では全体ではなく男女で層別した表のほうをみないといけないんだけど、それは性別と治療有無が交絡しているからである。性別を低血圧に書き換えた例ならば、全体の表も層別した表も、それぞれに価値がある(ここがPearlとちがう)。
　著者らもこの立場を支持する。つまり、第三の変数で層別すべきかどうかは、それがcausalな変数かどうかでは決まらない。
　なぜか？

　なぜならば... という説明がなされているのだけれど、これがさっぱり理解できない。難しいことが書かれているわけでないのだが、読み返しても話のポイントが掴めないのである。著者のかたは、変数間の因果関係が分かっているとき (DAGが描けるとき) に因果関係の方向と強さを調べるという状況と、それ以外の多種多様な状況とをごっちゃにしているのではないかと思うのだけれど... きっと私がなにか理解し損ねているのだと思う。

論文：データ解析(-2014) - 読了: Armisted (2014) 第三変数の復活

2014年3月 5日 (水)

　消費者行動論の教科書をめくると、かつて精神分析の影響を受け、深層的動機づけによって消費者行動を理解しようという立場がありました、しかしやがて廃れました。というような記述がみつかる。しかし面白いことに、市場調査の周辺で働いてみてわかったのは、そういう深層心理学的(ないし、疑似-深層心理学的)な消費者理解の枠組みが、案外な規模のビジネスになっている、ということである。
　調査会社のなかには、深層的動機づけのなんらかのモデルに基づき、調査手法を体系化しパッケージとして提供しているところもある。TNS(Kantar Group)が提供するNeedScopeと、Ipsosが提供するCensydiamが有名であろう。どちらも、あらゆる消費者行動の背後にある潜在的動機づけを二次元空間で理解するという枠組みに基づき、定性・定量両面での豊富な調査方法論を提供している。好き嫌いはありましょうが、こういうソリューションを提供できるのは、さすがグローバル・ファームだと思いますです。
　それにしても、ああいったソリューションで想定されている二次元空間って、いったいどういう背景から生まれてきたものなのだろうか？ ... という疑問を抱いてはや数年。紆余曲折あって、ついに下記の文献を発見したはいいものの、今度は入手の方法がなくて...

Heylen, J.P., Dawson, B., Sampson, P. (1995) An implicit model of consumer behavior. Journal of the Market Research Society, 37(1), 51-67.
　散々苦労してようやくコピーを手に入れた。この雑誌、泡沫誌ではないはずだが(IJMRの継承前誌)、電子サービスが閉鎖的なのである。
　論文といっても著者らは実務家で、要するにこの分野はアカデミックな消費者研究と少し離れているということであろう。Webであれこれ調べた結果、第一著者のHeylenはヨーロッパ出身、ニュージーランドで市場調査の専門家として活躍。90年代にはHeylen Research Centreという会社を経営していたが、1994年に清算したらしい。HeylenさんはIMPSYSという定性調査ソリューションを開発、NFOという調査会社にライセンス提供していたようだが、2003年にNFOはTNSに買収され、2008年にTNSはWPP傘下のKantar Groupに買収される。さて、1994年にはニュージーランドのFocusという会社(現存する)がNeedscopeを開発、どこかの段階でTNSに売却かライセンス提供したらしいのだが、2004年の記事によれば、TNSはNeedscopeとIMPSYSを併合して販売するとあるから、結局IMPSYSはNeedScopeの前身ということになりそうだ(間違っていたら申し訳ないです)。この論文のなかの図にはIMPMAPという商標がついているが、IMPSYSとの関係はよくわからない。なお、Heylenさんは2003年のインタビュー記事があるし、Heylen Internationalという会社は現存している模様。

　著者らいわく:
　消費者のニーズと行動の基本的ダイナミクスを構成するのは、生得的で潜在的な内的エネルギーである(←言い切ってる！いとも軽々と！！)。その同定と理解こそが、マーケット・リサーチがもっとも優先すべきことなのだ。ところが、その発見のために定性リサーチャーが行ってきた手法は体系的・客観的・科学的基盤を欠いている。
　そこでThe Implicit modelを提案する。このモデルによれば、すべての消費者行動は生得的な生物エネルギー原理、フロイトのいうリビドーに起因する。意識下において、この原理と発達を通じて獲得された社会化との間の緊張が生じる。この緊張が適応的フィルターを通って、情緒的反応(イメージとか)、行動(購買とか選好とか)、認知的反応(信念とか価値とか)、の3つのかたちで発現する。
　意識下の生物力動的動因は、表出・外化されるか、抑圧・内化されるかのどちらかである。また外化・内化を問わず、それは能動的・自己主張的なモードをとるか、受容的・社会親和的なモードをとるかのいずれかである。というわけで、あらゆる行動がそこに含まれる2次元空間を考えることができる。縦軸は生物学的次元(北が表出, 南が抑圧)、横軸は社会的次元(西が能動的, 東が受容的)である。
　この空間をピザみたいに8分割し、名前をつける。北から時計回りに、extroverted, warm, affiliative, subdued, introverted, cool, assertive, energeticである。
　この枠組みにしたがって、投影法のような定性的データ収集を体系化できる。定量的データ収集も体系化できる。
　このシステムは神経解剖学とも関係していて... (なんだか読んでて切なくなっちゃうので省略。諸行無常の響きあり。まあとにかく、大脳皮質だけが脳じゃない、というようなごくごく大雑把な話)

　ようやく現実的な話になりまして...
　すべての製品カテゴリについて、「理想のブランドの位置」も現実のブランドもコンセプトもパッケージも名前も広告も、はたまた属性セットも、この8つの領域からなる潜在的空間に位置づけることができる。ただし、そのためにはカテゴリごとの再解釈が必要である。たとえばビールのベネフィットならこんな感じ。

　この空間は、カテゴリを問わず一定、また製品開発プロセスのフェイズを問わず一定なので、便利である。
　定性的データ収集は投影法で行う。道具として、ascription sets(ヒトの顔写真)、gratification sets(絵のセットらしい)、animation set(動物や架空世界の絵らしい)を用いる。定量的データ収集にもこれらの道具を用いる。
　定性調査での解釈はこのモデルのダイナミクスの完全な理解を必要とする。定量調査の分析アルゴリズムは我々が開発済みである。
　云々。

　えーっと、その、。。。
　論文というより営業資料に近い内容だが、いやいや、文句を言ってはいけない、こういうドキュメントを残してくれただけでありがたい。発想がわかって勉強になりました。
　まあ、とにかく！こういう普遍的な概念枠組みを持っているというのは立派である。それに、あらゆる製品カテゴリで余人に代えがたい洞察を発揮する口八丁手八丁のスーパースター的リサーチャーが所長をやっていても、リサーチ･ファーム全体の消費者理解の質が上がるとはいえないわけで、大事なのは方法論の体系化である。その意味で、モチベーションというレベルにおいて消費者理解のための共通言語を作ろうとするこういう発想は素晴らしいし、そこにこそ有用性があるのだと思う次第である。たとえ２軸に納得できなくとも、たとえ８領域に納得できなくても。たとえ「すべての消費者行動は生得的エネルギーに基づく」と無根拠に言い切られようが、たとえリビドーがどうこうという反証不能な理屈を持ち出されようが。たとえ「縦軸はゾロアスター教、横軸はアメリカ･インディアンの聖なる教えに由来します」と云われようが。(すいません冗談です)

論文：マーケティング - 読了: Heylen et al. (1995) 消費者モチベーションの空間モデル

2014年3月 4日 (火)

Schwarz, N. (2007) Cognitive Aspects of Survey Methodology. Applied Cognitive Psychology, 21, 277-287.
　80年代初頭に米の調査法研究者らのあいだで提唱されたCASM(Cognitive Aspects of Survey Methods)アプローチについての概観。App. Cog. Psy. のこの号はCASM特集号で、これはよく巻頭に載っているような、以降の論文の露払いなんだけど、CASMも提唱されてから随分と月日が経っているから、その蓄積が紹介されていてなかなか面白い。それに短いし。というわけで、既読(のはず)だが、仕事の都合で再読。
　いくつかメモ:


論文：調査方法論 - 読了: Schwarz (2007) CASMの四半世紀

2014年3月 1日 (土)

佐藤俊哉 (1993) 疫学研究における生物統計手法. 日本統計学会誌, 22(3), 493-513.
疫学(というか、リスク要因への曝露の効果の研究) における統計手法についての啓蒙的レビュー。仕事上でちょっと悩んでいることがあって、頭を整理したくて読んだ。著者はなにしろ、他の惑星の卒論発表会に招かれ、思わず正論を述べて「しまりす」くんの大学卒業を阻止するという、非情にして怖れを知らない先生であって(「宇宙怪人しまりす」シリーズを参照)、啓蒙的文章に関してこの先生の名前は私のなかで絶対のブランドなのである。
いくつかメモ:

最後の今後の展望のところで、「少し技術的な問題としては、疾病発生割合の差や比、疾病発生率の差に関する回帰モデルの開発が、特にsparse-dataについて、望まれる」とある。まさにそういうのを探してるんです...

論文：データ解析(-2014) - 読了：佐藤 (1993) しまりすのための曝露効果研究法レビュー

« 2014年2月 | メイン | 2014年4月 »

rebuilt: 2022年8月13日 15:07
validate this page