Baucells, M., Sarin, R.K. (2010) Predicting Utility Under Satiation and Habit Formation. Management Science, 56(2), 286-301.
　研究会で経済学の先生が引き合いに出していた論文。なんだか面白そうだし、仕事と直接に関連しない論文を読むのは楽しいなあ(現実逃避)… と思って読み始めたんだけど、残念ながら途中で力尽きた。

1. イントロダクション
　現在の消費は将来の消費にどのように影響するか。次の2つが考えられる: (1)飽和(将来の満足が減る), (2)習慣形成(将来の限界効用が上がる)。
　割引効用(DU)モデルでは消費の独立性が仮定される。飽和や習慣形成を説明するための修正案もいくつか提案されてきた(それぞれSAモデル、HAモデルと呼ぶ)。心理学では、飽和と習慣形成は感受性減少と順応のあらわれだと考えられている。
　本論文は習慣形成と飽和の両方を組み込んだモデル(HSモデル)を提案する。

2. 習慣形成と飽和のモデル
　一連の消費を\(x_1, \ldots, x_T\)とする。[論文中ではそうなってないけど、いちいち\ldotsと書くのが面倒なので、このメモではベクトル\(\mathbf{x}\)と略記する。でもいちいち\mathbfと書くのも面倒なんだけどな]
　
(DUモデル)
　得られる総効用は、DUモデルではこうなる。効用を\(v(x_t)\)として$$ V_{DU}(\mathbf{x}) = \sum_t^T \delta^{t-1} v(x_t)$$ これだと、習慣形成も飽和も説明してないですね。現在の消費の効用が過去の消費から独立だから。
　以下、期ごとに経験された効用を\(v(x_t)\)とする。割引は考えない。話を簡単にするためでもあるし、規範的にいえば、経験された効用は割り引かれないからでもある。

(HAモデル)
　習慣形成についてWathieu(1997)のモデルを採用する。習慣化された消費レベルを\(r_t\)として、$$ V_{HA}(\mathbf{x}_t) = \sum_t^T v(x_t – r_t)$$ $$ r_t = r_{t-1} + \alpha(x_{t-1} – r_{t-1}) $$ \(0 \leq \alpha \leq 1\)は習慣化速度を表し、0だったらDUモデルになる。なお\(\alpha\)は財によって異なるものとする。

(SAモデル)
　飽和について。Baucell & Sarin(2007 OR)に従い、効用は現在の飽和レベル\(y_t\)からの増大によって決まると考えて$$ V_{SA}(\mathbf{x}) = \sum_t^T \left( v(y_t + x_t) – v(y_t) \right) $$ $$ y_t = \gamma(y_{t-1} + x_{t-1})$$ [1本目の式、原文では\( \sum_t^T v(y_t + x_t) – v(y_t) \)なんだけど、それだと総和記号のスコープがわかりにくいので勝手に書き換えた]
　\(0 \leq \gamma \leq 1\)は飽和速度で、0ならDUモデルになる。飽和は時間の経過とともに弱くなる。その半減期は財の性質に依存する。飽和水準はそれまでの消費の割引の累積となる。つまり$$ y_t = \sum_{s=1}^{t-1} \gamma^{t-s} x_s + \gamma^{t-1} y_1$$ となる。

(HSモデル)
　統合します。$$ V_{HS}(\mathbf{x}) = \sum_t^T \left( v(y_t – r_t + x_t) – v(y_t) \right) $$ $$ y_t = (y_{t+1} – r_{t-1} + x_{t-1})$$ $$ r_t = r_{t-1} + \alpha(x_{t-1} – r_{t-1})$$ [SAモデル同様、1本目の式は勝手に書き換えた]
　\(v(0) = 0\), \(v\)はS字型とする。Kahneman & Tverskyに従い損失のほうが急だとする。特記無い限り\(r_1 = y_1 = 0\)とする。
　\(\gamma=0\)にすればHAモデル、\(\alpha = 0\)にすればSAモデル、両方ゼロにすればDUモデルになる。
　このHSモデルは以下の特徴を持っている:

• SAモデルの単純な拡張。消費の絶対水準を、参照水準に対する水準に変えただけ。
• 心理学的に魅力的。
• SAモデルと同じくlocal substitution特性(たとえば刺激(2,0)と(1,1)の効用が、2時点の間隔が0に接近するにつれて等しくなること)を持つ。
• HAモデルでもSAモデルでも説明できない現象を説明できる。後述。

3. 望ましさ、満足、離脱症状
　HSモデルでは、消費の望ましさ(金の効用が準線形ならWTP)は、消費から予期される満足と、先行する消費によって経験される撤退の苦痛によって決まる。飽和レベルと習慣レベルを\(y, r\)としよう。消費の望ましさは消費の効用と非消費の効用の差 $$ \mathrm{Desirebility} = v(y – r + x) – v(y-r) $$ 満足は $$ \mathrm{Satisfaction} = v(y – r + x) – v(y)$$ 非消費時の不満をwithdrawalと呼ぼう[離脱症状と訳することにする]。$$ \mathrm{Withdrawal} = -( v(y-r) – v(y) )$$ 望ましさは満足と離脱症状の和である。

　[ここでひとしきり、図を用いた説明がある。恐縮ながら図を貼らせていただきます。

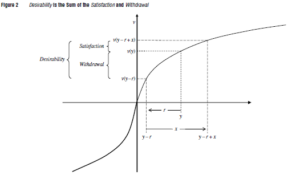
　話の要点を自分なりにまとめておこう。上の図の横軸は内的状態、縦軸がその状態の効用である。状態は効用関数とは無関係に、消費の履歴によって決まる。
　3つの状態変数を考える。

• (a)「飽和レベル」\(y\)。前期の(c)に繰越率を掛けたものとなる。
• (b)飽和レベルから「参照レベル」を引いた値\(y-r\)。参照レベル\(r\)は自己回帰過程に従い、そのイノベーションは(前期の刺激-前期の参照レベル)x学習率である。
• (c)(b)から出発し、消費の分だけ右に動いた値\(y-r+x\)。

　この3つの状態に対応する3つの効用がある。(a)の効用から(b)の効用への減少\(v(y)-v(y-r)\)が「離脱症状」。(a)の効用から(c)の効用への増大\(v(y-r+x)-v(y)\)が「満足」。

3.1 安定的消費の元での望ましさの3つのフェイズ
　\(x_t\)がずっと1だったときの望ましさの時系列\(D(t) = v(y_t – r_t + 1) – y(y_t -r_t)\)を調べよう。
　まず、飽和によって\(D(t)\)は下がっていく。しかし習慣形成がはじまると上昇に転じる(転じる時点を\(t^*\)とする)。長期的には飽和する(飽和に達する点を\(t^{**}\)とする)。
\(t^*, t^{**}\)の値は\(\gamma, \alpha\)に依存し、場合によっては各フェイズはスキップされる。

3.2 渇望(craving)
　欲求の非充足が蓄積され\(y\)が原点の左に行くと渇望が生じる。[原点の左の方が関数が急だから。いろいろ書いてあるけどパス]

3.3 習慣形成が飽和を軽減する
　[めんどくさくなってきたので少し中略して…]
　現在の消費\(x_s\)が将来の効用に与える影響は3つある。(1)将来の習慣消費レベルを増大させ、効用を減らし、限界効用を増やす。(2)将来の飽和レベルを増やす。(3)飽和と習慣形成の交互作用。習慣形成は飽和を軽減する。この点についてはアダム・スミスも指摘しているぞ。

[ここから読んでない。見出しのみメモする]

4. 離散選択問題
　HSモデルは習慣維持(多く得るとより欲しくなる)とバラエティ・シーキング(多く得ると欲しくなくなる)の葛藤を説明している。
　[… 単純な離散選択問題を定式化して、習慣維持とバラエティ・シーキングの両方が起きることを示しているのではないかと思う。読んでないけど]

5. 最適消費水準
　[… 離散選択問題を拡張して量にしている。うん、まあこの話はいいや。パス]

6. プロジェクション・バイアス
　HSモデルは規範モデルで、消費者が現在の選択の将来の効果を合理的に選択しているかどうかは別の問題である。おそらく、消費者は将来の飽和と習慣化レベルについて現在のレベルと同様に予測してしまっているだろう。
　Simonson(1990 JMR), Gilbert(2006 書籍)いわく、被験者は消費の前にはバラエティを好むけれど実際の選択においては変化しないほうを好む。それはこのモデルでいうと…[パス]

7. 結論
　[…]
本研究の目的は、通常の効用モデルと整合するようなパターン以外の、たくさんの選好・消費パターンを模倣し合理化するような2パラメータモデルを作ることあった。本モデルから生成されるパターンは心理学とか意志決定研究とかで観察されているのと整合的である。
　今後の課題: (1)HSモデルが時間的不確実性の文脈で持つ含意。(2)well-beingと幸福研究における含意。(3)HSモデルの項理論的懸鼓湯。(4)実証研究での検証。飽和と習慣化レベルは過去・未来の消費のもっと複雑な関数かもしれない。[ああそうか。(\(\alpha\)と\(\gamma\)ってもっと複雑かもね]
　云々。
　
————
　ううううう… きっとわかりやすい論文なのだろうと思うし、もっと本腰をいれて読めばよかったのかもしれないけれど、正直なところ、\(y, r\)の実質的意味について考えはじめたら頭が混乱し躓いてしまったのである。そのため半年ほど放置してしまった。整理がつかないから無理やり最後までめくったけど、理解できたとはいいがたい。

　どこで混乱したかというと…
　顧客満足の期待-不一致モデルによれば、満足は期待と知覚品質の差で決まりますよね。昔懐かし順応水準理論を思い出すと、判断というのは順応水準と刺激知覚の差で決まりますよね。
　このモデルに対応づけると、期待なり順応水準なりが\(y\)、知覚品質なり刺激知覚なりが\(y-r+x\)だ。\(r\)とは、現在の消費量\(x\)がゼロのときに陥る内的状態\(y-r\)と、期待・順応水準\(y\)との差のことだ。現在の状態を期待・順応水準に到達させるためにいま必要な消費量といってもいい。
　ところがこの論文では、この\(y, r\)を「飽和レベル」「参照レベル」と呼んでいるのである。そこのところでわけがわかんなくなってしまったんだと思う。

　途中で力尽きたもうひとつの理由は、最後まで実証分析が出てこないという点。そういうのって読んでて気分的に辛い。要するに根性がないという話である。