2020年4月21日 (火)
2004年12月からなんとなく続いてきたこのブログでございますが(まじか...)、このたび移転いたします。
引っ越し先はこちらでございます。
2020年4月17日 (金)
Tashman, L.J. (2000) Out-of-sample tests of forecasting accuracy: an anlysis and review. International Journal of Forecasting, 16, 437-450.
仕事の都合で読んだ奴。時系列予測の交差検証をどうやるかという話。
2000年の論文というと、結構最近のだなと感じてしまうのだけれど、これは私の感覚が狂っているからで(平成生まれの子ってせいぜいまだ中学生くらいまでだろうという気がしませんか?)、考えてみればこれって20年前の論文なんですね... やれやれ...
1. イントロダクション
[略]
2. in-sample評価 vs. out-of-sample評価
in-sampleの誤差は予測誤差を過小評価しやすい。一期先予測を繰り返して補外するタイプの予測手法(指数平滑化とか)ならなおさらである。また、in-sample適合で選択した手法はpost-sampleの最良予測でない。
post-sample予測精度を確かめるひとつの方法は待つことだが、さすがに現実的でないので、ふつうはホールドアウトを使う。つまりfit期間とtest期間をわけるわけである。
3. fixed-origin手続き vs. rolling-origin手続き
fit期間の最後の期$T$をforecasting originという。そこから予測したい期までの期間をlead timeとかforecasting horizonという。test期間を$N$とする。つまり最長lead timeは$N$期先予測である。
$T$に立って$T+1$から$T+N$を予測するのをfixed-origin評価という。予測実績を得るためには長いtest期間が必要になるし、originをどこにとったかに影響されるし、lead timeを通じた誤差を平均すると短期予測誤差と長期予測誤差を混ぜちゃうことになる。
これに対して、originをどんどん更新していくやり方をrolling-origin評価という。たとえば$N=4$だったら、まず$T$に立って4つの予測値を得て、次に$T+1$に立って3つの予測値を得て... 計10個の予測値を得る。[あれ?ちょっと混乱しちゃったのでメモしておくけど、たとえば$T+1$に立つときは時点$T+1$の実現値を参照するってことだよね? つまりホールドアウトしたテスト期間についてもこっそり実現値を使うってことであってるかな?]
rolling-origin評価の場合、各lead timeごとの正確性を評価できる。さらに、あるlead timeについて予測の経験分布を得ることができる。
4. out-of-sample評価を実装する際の諸問題
- 一番大事なのは、fit期間とtest期間をどうわけるかである。まず、最長で何期先予測が必要かを考慮する必要がある。$H$期先予測まで必要なら$N$はそれ以上でないといけない。さらに、$H$期先予測が最低いくつほしいか($M$)を考える。$N$は$H+M-1$以上でないといけない。分布が欲しければ$N$をもっと長くとらないといけない。
- originをupdateするとfitするデータ点が増えるが、そのたびに予測式も変える(recalibration)ほうがよい。回帰モデルの場合でいえば、recalibrationのないupdateというのはfixed-origin評価と同じことになる。[ああそうか。recalibrationなしというのは、パラメータを固定して学習データ点だけ増やすことを意味しているわけで、単純な回帰モデルの場合はoriginを$T$から$T+1$に移動しても$T+2$の予測値は変わらないが、ARMAモデルだとちょっと変わるね]
- rolling-originデザインでは特定のoriginを選択したことによる影響を取り除ける。ここで大事なのは、はずれ値への敏感性は下がったが、ビジネスサイクルのフェイズへの敏感性は下がってないということだ。test期間はビジネスサイクルの特定の期間だけを反映しているかもしれない。それがいやなら、test期間を複数設けてそれぞれについて誤差を評価すると良い。
- originをupdateするたびに古い時点をひとつ捨てるという手もある(rolling windowsとかrolling sampleという)。ふつうはその必要はない。たいていの時系列手法は遠い過去のデータの影響をあまり受けないから。
5. sliding simulations
手法の選択と評価にrolling-originデザインを使うというアイデアもある。sliding simulationとかrolling horizonという。
時系列をまず前半(fit用)と後半(test用, $N$個)にわける。で、前半をさらに、in-sample fit期間の$T$個とpost-sample fit期間の$P$個にわける。
[この段落よくわかんないので逐語訳] sliding simulationは、検討している手法のそれぞれについての、rolling out-of-sample評価のペアを伴う。第一の評価では、スムージング・ウェイトをpost-sample fit期間へと最適化し、それぞれのlead時間について最良の手法を選ぶ。第二の評価はテスト集合に対する評価で、この手法によって得られた予測の正確性を評価するという伝統的な目的のために行う。[えええ? 予測手法AとBがあるとするじゃないですか。最初の$T$期でそれぞれのパラメータを推定しますわね。次の$P$期でそれぞれの予測性能を評価し、良かったほうを選ぶ。最後の$N$期で選んだほうの予測性能を評価する。次に、最初の$T+1$期で推定、次の$P$期で選択、最後の$N-1$期で評価。という風に繰り返すのだろうか。ってことは、leadごとに手法を変えるってこと?]
[実証研究の紹介... Makridakis(1990 Mgmt.Sci.), Fildes(1989 Mgmt.Sci.), Weiss & Anderson (1984 JRSS)というのが挙がっている。この話、この論文であれこれ考えてないで、Makridakisの本とかを調べたほうが早そうだな。よってメモは省略]
6. 複数の時系列: 予測コンペティション
[この節、M-competiton以降の一連の予測コンペティションの話を中心にして書かれているんだけど、いま関心ないのでそれらについてはメモを省略し、面白い部分だけメモする]
単一時系列でわざわざrolling originsを使うのは、それぞれのlead時間について十分な予測を得るため(adequacy)、そして特定の出来事なりビジネスフェイズなりへの誤差指標の感度を下げるため(deviersity)、である。
時系列が複数ある場合、adequacyを得るためには、なんらかの特性において等質なcomponent seriesを選ぶ必要がある。またdiversityを得るためには、性質においてもカレンダー時間においても異質な時系列をたくさん集める必要がある。こういう立場では、originは固定し、テスト期間を単一にすることが多い。
いっぽう、特性のタイプの時系列(例えば産業別の年次売上数量)をうまく補外できること(selectivity)を主目的とすることもある。この場合は、時系列はそんなにたくさん集めず、diversityのためにはrolling originsを使いテスト期間を複数にすることが多い。[...ちょっと飛ばして...]
複数の時系列を使う場合、長さやカレンダー時間は異なっていてよいが、test期間の長さはふつう揃える。予測誤差統計量は異なる時系列を通じて平均したり、異なるlead時間を通じて平均したり、両方を通じて平均したりする。
予測誤差統計量の選び方については、Armstrong & Collopy (1992 Int.J.Forecasting), Fildes(1992, Int.J.Forecasting), Ahlburg et al. (1992 Int.J.Forecasting)を参照せよ。
異なる時系列を通じて平均する場合は、スケール依存な指標(RMSEとかMADとか)は避け、スケール独立な指標(APEとか)を使うべし。ただし、元の値が0に近いことがあるときパーセント誤差はすごく歪む。そういうときはMAPEよりAPEの中央値がおすすめ。symmetric MAPEというのもあるよ。volatalityが変動するときはさらに工夫が必要で...[中略。まあ必要になったら調べよう]
異なるlead時間を通じて平均する場合、ないし時系列とlead時間の両方を通じて平均する場合、通常は単純に足し上げるが(短いleadに重みがつくことになる)、個々のlead時間ごとにMAPEをとったうえでlead時間を通じて(重みつき)平均を出してもよい。
ところで、originによって(ないしカレンダー時間によって)モデルも変えるべきだ、変えるべきだという可能性もある[...]。
手法の予測の正確性についてわかったとして、ではどうやって手法を選ぶか。自動で選ぶという提案もあって[...]。
最近では時系列の階層構造を考慮するという試みもある。Bunn & Vassilopulis(1993 Int.J.Forecasting)をみよ。今後の課題である。[短い説明なのでわからんが、階層時系列回帰をイメージすればいいのだろうか]
7. 予測ソフトウェアにおけるout-of-sample評価
[略]
8. サマリー
[略]
...細かいところに深入りしない広く浅く型のレビューなので、ちょっとストレス貯まったが、ま、勉強になりましたですー。
論文:データ解析(2018-) - 読了: Tashman (2000) 時系列予測の交差検証戦略
2020年4月13日 (月)
仕事の都合で先月とったメモ、なんだけど、読み返すと、なんだかすごく昔のできごとのような気がする。この1か月間の間に、世の中どれだけ変わったことだろうか。
Jamieson, L.F., Bass, F.M. (1989) Adjusting stated intention measures to predict trial purchase of new products: A comparison of models and methods. J. Marketing Research, 26(3), 336-345.
いわく。
市場調査では購入意向(PI)のデータをよく使う。PIで実購買を予測する研究はいっぱいあって,
- frequently purchased branded products ... Penny et al. (1972 J.MarketRes.Soc.), Gormley(1974 J.MarketRes.Soc.), Tauber (1975 JAR), Warshaw (1980 JMR)
- generic established consumer durable products ... Juster(1966 JASA), McNeil(1974 JCR), Adams(1974 JCR)
結果をまとめていうと、PIは実購買と正の相関を持つが、実購買の予測力は低い。なんとかならんもんか。
この問題、製品タイプで分けて調べたり、新製品か既存製品かで分けて調べたりする必要がありそうだ。
- Kalwani & Silk (1982 Mktg.Sci.): 耐久財と非耐久財との差を示している。
- Granbois & Summers (1975 JCR): 対象者のタイプより製品カテゴリで差があった。
- Sewall (1978 JMR), Urban & Hauser (1980 書籍): 新製品の研究。
なお、Silk & Urban (1978) みたいな上市前売上予測は予測力が高いけど、PIだけつかっているわけではないし、トライアル購買ではなくて市場シェアを予測していたりする。
かつてJohnson(1979, Working Paper)は、市場調査のサプライヤー、コンサル、広告代理店に調査をかけ、どんなPI指標を使っているか、その妥当性を調べたことはあるかと訊ねた。その結果、もっともよく使われているのは次の5件法であった: Definitely will not buy, Probably will not buy, Might/might not by, Probably will buy, Definitely will buy.
というわけで、本研究ではこの5件法PI尺度をつかった3つのモデルを比較する。
選手入場です。
選手1. ウェイティング。
5件法の上から順にウェイト$w_i$を振る。対象者数を$N$、各段階の人数を$n_i$として、
$Pr(Trial) = \sum_{i=1}^5 w_i (n_i/N)$
Johnson(1979)は実務家に、あなたがお使いのウェイト値についても訊ねていた。回答に出てきたのは次の6通り。Topboxから順に
- 1) 1, 0, 0, 0, 0
- 2) 0.28, 0, 0, 0, 0
- 3) 0.8, 0.2, 0, 0, 0
- 4) 0.96, 0.36, 0, 0, 0
- 5) 0.70, 0.54, 0.35, 0.24, 0.20
- 6) 0.75, 0.25, 0.10, 0.05, 0.02
Morrison(1979 J.Mktg)は、真の意向を$I_t$, 言明された意向を$I_x$として、(1)$I_x$はパラメータ$I_t, n$の二項分布に従う, (2)$I_t$は母集団を通じてベータ分布に従う、と仮定した。
$E(I_t|I_x) = (\alpha/\alpha + \beta + n) + (n/\alpha + \beta + n) I_x$
ただし$I_x = x / n$で、$x$は$0$から$n$までの整数。
さらにこのモデルを修正し、実購入確率を$P_x$、真の意向の変化を$\rho$, 系統的バイアスを$b$として、
$P_x = A + BI_x$
$A = [\rho \alpha(\alpha + \beta)] + [(1-\rho) \alpha / (\alpha + \beta + n)] - b$
$B = [(1-\rho) n / (\alpha + \beta + n)]$
[上の式は原文のままメモしたが、これではなにがいいたいのかさっぱりわからないではないか! 以下、自分なりに補足してみよう。
PIを$n+1$件法尺度で訊いたときのある人の回答を、5件法なら4, 3, 2, 1, 0とコーディングし、これを$x$とする。$I_x = x / n$とする(5件法なら上から1, 0.75, 0.5, 0.25, 0)。$x$が試行回数$n$の二項分布に従うと捉え、成功確率を$I_t$とする。$E(I_x|I_t) = I_t$である。
さて、$I_t \sim Beta(\alpha, \beta)$と考える。つまり事前分布の平均は$E(I_t) = \frac{\alpha}{\alpha + \beta}$である。成功確率$I_t$の試行を$n$回行い成功回数が$x$だったんだから、事後分布は$Beta(\alpha+x, \beta + (n-x))$となる。その平均は
$E(I_t|I_x) = \frac{\alpha+x}{\alpha+\beta+n} = \frac{\alpha}{\alpha+\beta+n}+I_x \frac{n}{\alpha+\beta+n}$
さらに、実購買確率は
$P_x = \rho E(I_t) + (1-\rho) E(I_t|I_x) -b $
だと考える。つまり、調査時点の態度$E(I_t|I_x)$から少しだけ$E(I_t)$のほうに戻ってしまい(その程度を表すパラメータが$\rho$)、さらにバイアス$b$だけずれる、と考えるわけだ。
...ってことですよね!? きちんと書いてくださいよ、もう...]
選手3. 線形モデル。
5件法で訊く($I_x$)と同時に101件法でも訊いちゃう($P_x$)。で、
$Pr(Trial|Intentions) = \sum_x Pr(I_x) Pr(P_x|I_x)$
$Pr(Trial) = k Pr(Trial | Intentions)$
とする。
[ちょっとよくわからんのだが、脱力しちゃって真面目に考える気にならない。これってPIの設問が増えてんじゃん... 比較にならないじゃん...]
選手2の$\rho$と$b$、選手3の$k$を決めるために、本研究では製品知覚の項目を使う。すなわち、認知(4件法)、好意(5件法)、購入容易性(4件法), 誰かに相談するか(二値)、購入可能性(お店でみたことがあるか。2件法)。
というわけで、実験でございます。
M/A/R/Cに実査を頼んで電話調査をやった。対象者は世帯の買い物をしている女性。同一対象者に3ヶ月あけて3回調査。順に800, 412, 200人。以下では3回とも答えた200人について分析する。
製品は10個、カテゴリは歯磨き、ダイエット飲料、フルーツスティック、パソコンなど10種類(うち5つは耐久財)。製品特徴は提示するけどブランド名は出さなかった。だいたいひとり5製品について聴取した(延べで921製品x人)。wave 1でむこう6ヶ月PI、wave 2でトライアル購入有無とむこう3ヶ月PI, wave3でトライアル購入有無を訊いた。
結果。
PIとトライアル購入の間には正の相関があった。非耐久財のほうがやや高かった。
選手1について。重みづけ合計と実トライアル購買率を比べると、6)がいちばんましだったけど(MAEは9.87パーセントポイント)、大差なかった。
選手2について。まず最尤法で$\alpha$と$\beta$を推定する。で、それと観察された$P_x$から$\rho$と$b$を求めることもできるんだけど、そうすると$P_x$の予測には使えないわけなので[ああそうか。著者らは$\rho$と$b$も製品ごとに推定しようと思っているのだ]、まず当該製品以外の9製品の$P_x$を使って$\rho$と$b$を推定し、それらを5つの製品知覚項目に回帰した。結局、$\hat{\rho}$の説明変数として相談有無と購入可能性、$\hat{b}$の説明変数としては好意度と購入可能性を採用した。そんなこんなで$P_x$が予測できるようになった。性能は良くなった(MAEは3.9パーセントポイント)。
選手3について。[...めんどくさいので中略...] 性能はさらに良くなった(MAEは2.3パーセントポイント]。
というわけで、実トライアル購買の予測に際しては単なるウェイティングじゃなくて、補助的な変数も使ったほうがいいのではないでしょうか。云々。
...うーん...
これ要するに、購入意向の5件法回答だけじゃなくて事後の店頭接触経験を考慮したほうがトライアル購入率を正確に予測できたよ、5件法と一緒に確率評価をさせればもっと正確になったよ、って話ですよね。えーっと、そりゃまあ、そうでしょうね...
申し訳ないけど、よく載ったねえ、というのが正直な感想である。確かに選手2のモデルは勉強になったけど、この論文のオリジナリティというわけではないだろう。おそらく、当時はこういうデータを集めるのがすごく大変だったから、これでも論文として成立したのではないかと思う。
まあ、ヒストリカルな意味ではすごく面白かったし(特に選手1のところ)、仕事の役に立つ内容だったので、文句はないんですけど...
いくつか追加でメモしておくと...
- 考えてみると、最初に新製品かどうかでちがうとかカテゴリによってちがうとかいっておきながら、結局はひとつのモデルで済ましてんのね。まあいいけどさ。
- 引用されているJohnson(1979)という研究、すごく面白いので、ちょっと調べてみたんだけど、引用文献によればアリゾナはPheonixにあるArmour-Dial Co.という会社のprivately cirlulatedなワーキングペーパーである由。この会社はおそらくDialという石鹸をつくっている会社であろう。著者Jeffrey Johnsonについてはよくわからない。ワーキングペーパーの題名"A study of the accuracy and validity of purchase intention scales"で検索すると、これを引用している論文がこの論文以外にもいくつかみつかる: Holak(1988 J.ProductInnov.Mgmt.), Whitlark, Geurts, & Swenson (1993 J.Business Forecasting Methods & Systems), Repace & Gertner (2013, J. MktgPerspectives)。これら全部が原文を確認せず孫引きしているとも思えないので(楽観的過ぎますかね?)、実在したワーキングペーパーなのだろう。手に入れられそうにないのが残念だ。
- イントロの最後のところに、「調査で質問することで、回答者たちのその後の実購買が変わるんじゃないか」という予想されるツッコミについての防衛線が1段落ある。確かに相関は高めになるかもだけど、とにかくここで実購買を予測できることが必要条件でしょ、という言い分である。こういう質問-行動効果って、実証研究はSharman(1980)に遡るんだけど、この論文では引用していない。やっぱりマーケティング領域では、Morwitz, Johnson & Shmittlein (1993)のJCR論文が出るまで、あまり知られていなかったんだろうな...
- 著者らの研究というより、先行するMorrison(1979)らのベータ二項モデルに対する疑問なんだけど、ある人の5件法の回答$x$がその人の真の態度を$p$として二項分布$B(4, p)$に従うという仮定は、さすがにちょっとどうかなと思う(自白すると、仕事でやむなくそういう強気なモデルを組んだこともあるんだけど、あれは後味が悪かった...)。$p$についてベータ分布を考えるときに話がスマートになるというのはわかるけど、回答誤差の分散が$4p(1-p)$になると決め打ちしていることになるでしょ。実質的な観点から見たリアリティに欠けるのではないか。いや、回答の認知過程についての諸仮定から演繹的に出てきたんですとか、SEMだかMMTMだかで回答誤差を評価したらどうやら分散は$4p(1-p)$に近いですとかだったら、その時は納得するけどさ...
論文:調査方法論 - 読了: Jamieson & Bass (1989) 購入意向で売上を予測する上手い方法
2020年4月 2日 (木)
前回に引き続き、今度はバッハ「ヨハネ受難曲」の全編演奏の動画を探してみた(音楽のみで画像は静止画、というのは除外)。
バッハ・コレギウム・ジャパン、鈴木雅明指揮、福音書記者James Gilchrist、2020年。先月ケルンで開かれるはずだったの演奏会が新型肺炎のために中止になってしまい、かわりに無観客でライブ配信したのだそうで、その録画。ここんところサブディスプレイでこれを流しっぱなしにして仕事している。ある意味、貴重な映像だと思うんだけど、これっていつまで観られるんだろう?
(2020/04/10追記: 昨日、バッハ・コレギウム・ジャパンがこの動画の演奏部分を切り出したものをYoutubeに投稿した模様。この動画は消えないと思うので、ついでに貼っておく)
コレギウム・ヴォカーレ、指揮フィリップ・ヘレヴェッヘ、福音書記者ジュリアン・プレガルディエン。2020年、リハーサルの録画で、モノラル録音じゃないかと思う。
英国のVOCES8というヴォーカルグループとエンシェント室内管弦楽団による演奏。指揮Barnaby Smith, 福音書記者Sam Dressel。2019年。教会での演奏なんだけど、前列に座っている子どもたちが退屈そうにしていて可笑しい。
Bach Collegium at Saint Peter's, 指揮はオルガン弾いているBalint Karosiさんという人、福音書記者Gene Stenger, 歌詞は英語訳。 2019年。コンサートではなく、ニューヨーク市Saint Peter's Churchの礼拝での演奏。最後は会衆全員の合唱。みんな体力あるなあ。コンサートならわかるけど、礼拝としては長くないっすか?
オランダバッハ協会、指揮はヨス・ファン・フェルトホーフェン、福音書記者はRaphael Hohnという人。2017年。原則35歳以下の音楽家たちによる演奏だそうな。単に聴いている側からみると年齢なんてどうでもいいような気がするんだけど、養成という意味では大事な取り組みなんでしょうね。
TENETとThe Sebastiansという音楽グループの演奏, 2017年。NYの教会での演奏で(礼拝というわけではない)、録音がいまいち。動画を全部見たわけではないんだけど、終わりごろには会衆のなかにぐったりしている人がいて、ちょっと同情した。椅子、固そうだしね。
ダニーデン・コンソート, 指揮ジョン・バット, 福音書記者ニコラス・マルロイ, 2017年。イギリスで毎年夏に、BBC Promsという大規模な音楽フェスがあるのだそうで、そこでの演奏。ここまで大規模だと、なんというかスーパーボールという感じで、ちょっと引いちゃいますね...
(2020/04/13追記) 一昨日投稿されたものを発見。説明がハンガリー語なんだけど、えーっと、Budafoki Dohnányi Zenekar, 指揮ガボール・ホッレルング(Hollerung Gábor), 2017年。ハンガリー語字幕付き。冒頭部分を観ただけなのだが、合唱者たちが不思議な芝居をするだけでなく、仏教のお坊さんやイスラム教徒も登場するという、これまた斬新なステージである。教会ではなくホールで上演しているが、コラールでは観客も合唱し始めたし、これはひょっとして音大生による上演なのかな?
Barockorchester Stuttgart(シュトゥットガルト・バロック管弦楽団、でいいのかな?)、指揮はフリーダー・ベルニウス、福音書記者はTilman Lichdiって人。2016年。
Stiftsbarock Stuttgart、指揮カイ・ヨハンセン、福音書記者はJan Kobowって人。2015年。
コンチェルト・ケルン、ペーター・ダイクストラ指揮、福音書記者はマクシミリアン・シュミット。演奏年不明。すごく安っぽいキャプションがついている野良アップロード動画で、2015年投稿だけど、映像の感じからするともっと古そうだ。→youtubeの解説欄をよくみると、この映像の権利はNAXOSが持っている模様。ひょっとしてこのDVDなのかしらん。だとしたら2015年の演奏だ。
Le Concert Etranger, 指揮Itay Jedlin, 福音書記者Vincent Lievre-Picard, 2014年。フランスはアンブロネという町で開かれた音楽祭での演奏。
イングリッシュ・バロック・ソロイスツ, 指揮はジョン・エリオット・ガーディナー。福音書記者はあのマーク・パドモア兄貴である(クラシックなんてからきしわかんないけど、この髭のおっさんはなんだかすごい)。おそらく2008年のBBC Proms。英語字幕付き。
バッハ・コレギウム・ジャパン、鈴木雅明指揮、福音書記者はゲルト・テュルクって人。2000年、サントリーホールでのライブ。英語字幕つき。
ミュンヘン・バッハ・コレギウム, エノッホ・ツー・グッテンベルク指揮。福音書記者はクレス=ホーカン・アーンショーという人。同じメンツでマタイ受難曲の動画もあったなあ。2015年投稿だがかなり古い演奏だと思う。
ウィーン・コンツェントゥス・ムジクス, 指揮はニコラウス・アーノンクール, 福音書記者はクルト・エクウィルツ。1985年。私この指揮者のヨハネ受難曲のCDをときどき聴いているのだが、この動画で聴くとちょっと違った印象である(語彙が貧困でうまく表現できない...)。調べてみたところ、このアーノンクールさんはヨハネ受難曲を三回も録音しているのだそうで、私のCDは1993年演奏。へー。
ミュンヘン・バッハ管弦楽団、カール・リヒター指揮、福音書記者ペーター・シュライアー。1970年。演奏と絵画が交互に映される、昔風の映像である。それはそれで味わい深い。英語字幕つき。
探せばまだまだありそうだけど、だんだん音大生とか地域の音楽サークルとかの演奏が増えてくるので、このへんで打ち止めにしよう。
2020年4月 1日 (水)
実にどうでもいい話ですが... すいませんこれは私による私のためのメモです。
年明けに、音楽学者・磯山雅の「マタイ受難曲」という本を読んだのがきっかけで、妙にバッハのマタイ受難曲にはまってしまい、仕事しながらずーっと聴いていた。ついには柄にもなく、たまたまみつけたコンサートのチケットまで取ってしまったのだが(クラシックのコンサートなんてどれだけプチブルなのかとびびりつつ)、そこでコロナ禍が来襲し、コンサートはあえなく中止、のみならず自宅から出られないという事態に陥った。
残念だなあ、とぼんやりyoutubeを眺めていたら、全編演奏の動画が結構あるので驚いた。ひとが口あけて歌っているのをみてなにが楽しいのかと思いますが、これが妙に楽しいんですね。冴えない感じのおっさんが天使のような歌声の持ち主だったりして。
というわけで、youtube上でみつかった、バッハ「マタイ受難曲」の全編演奏の動画を挙げておく(音楽のみで画像は静止画、というのは除外)。正確な演奏年はわからないのが多いんだけど、だいたい新しそうなのから順に。
いきなり再生回数の少ないやつから始まるけど、マレーシア・バッハ・フェスティバル・オーケストラ、David Chin指揮。2019年の演奏らしい。英語と中国語字幕付きというちょっと珍しいライブ動画である。1曲目の合唱の出だし、日本語で「来なさい娘たち、ともに嘆きましょう」は「来吧、女兒們、来興我們哀悼」なのだそうです。
オランダバッハ協会、指揮はヨス・ファン・フェルトホーフェン、福音書記者はベンジャミン・ヒューレットというイケメン。2019年投稿だから、2018-2019年ごろのライブであろう。映像としていちばん見ごたえがあるのはこの動画だと思う。ネットでの発信に力をいれているようで、他にもいろいろ説明が充実してそうだ。
コンセルトヘボウ室内管弦楽団, 指揮ヘイス・レーナース, 福音書記者Mikael Stenbaek, 2018年。
Bach Collegium at Saint Peter's, 指揮はオルガン弾いているBalint Karosiさんという人、福音書記者Gene Stenger, 歌詞は英語訳, 2018年。これはライブコンサートというよりも、ニューヨーク市Saint Peter's Churchの礼拝での演奏らしい。なので、3時間近くかかった演奏が終わると、会衆は拍手するどころか全員起立、お祈りと聖歌合唱である。へえええええ、こういう文脈で演奏されることもあるのか。これはちょっと貴重な映像であった。
Hofkapelle Munchenってかいてあるんだけど、ホーフカプレ?ってどういう意味なの? 指揮はChristian Fliegnerって人、福音書記者はBenjamin Glaubitzというお兄さん。世の中は広いもので、バッハの演奏を片っ端から調べてデータベースにしてくださっている奇特な方がいらして、それによれば2017年演奏だそうです。
イングリッシュ・バロック・ソロイスツ, 指揮はジョン・エリオット・ガーディナー。おそらく2016年ごろの演奏。福音書記者はマーク・パドモアという、他の動画にも出現するひげのおっさんで、音楽の素養もドイツ語の知識も全くない私だが、このおっさんの謎の説得力にはびびってしまう。この人が新聞の勧誘に来たら取っちゃうかも。
Verbier Festival Chamber Orchestra, Thomas Quasthoff指揮, 2015年。ヴェルビエってのはスイスのリゾート地らしい。指揮者が椅子に座ってるんでどうしたのかと思ったら、この方はもともとサリドマイド薬害で障害をもっていて、かつては有名な声楽家だったんだけど引退したんだそうな。福音書記者は... おっと、またマーク・パドモアだ。
説明がロシア語なのでさっぱりわかんないんだけど、機械翻訳によれば、「バッハ・アンサンブル」の演奏で、指揮はヘルムート・リリング。福音書記者のメガネのおっさんはローター・オディニウスという人かしらん? 2014年。
ロイヤル・コンセルトヘボウ管弦楽団, 指揮はイヴァン・フィッシャー、福音書記者はまたもマーク・パドモアさん、2012年。DVDやBlu-rayにもなっているらしい。このメモをとるために各動画の1曲目だけをそれぞれぼーっと聞いてたんだけど、この演奏にはすっかり引き込まれてしまい、2曲目、3曲目と進んで途中で止めようにもなかなか止められない、という感じであった。
コレギウム・ヴォカーレ・ゲント, 指揮はフィリップ・ヘレヴェッヘ, 福音書記者はクリストフ・プレガルディエンというおっさん。画面左上に「3sat」と書いているのを手掛かりに探したところ、どうやら2010年の演奏らしい。英語の字幕付き。
ベルリン・フィルハーモニー管弦楽団, 指揮サイモン・ラトル, 2010年。これはピーター・セラーズの謎の演出がついていて(いやいや、「博士の異常な愛情」のあのコメディアンじゃなくて。有名な演出家らしい)、合唱隊が歌いながらなんだかよくわからない芝居をする模様。忙しそうだなあ。16本にも分割されているので全部はみてないんだけど、2曲目にやおら立ち上がって歌い出す丸刈りの福音書記者は、なんと!マーク・パドモア兄貴じゃありませんか。
(2020/04/10追記: 調べてみたところ、DVDやBDも出てるし、ベルリンフィルのWebサイト(なんと日本語版がある)で金を払えばネットで見ることができる(なんと日本語字幕付き)。なんという商売上手。さらに、ただいま新型肺炎のため期間限定で観放題。なんという太っ腹。というわけで、さっそくサブディスプレイで流し始めたんだけど、あまりに斬新なステージでびびってしまい、仕事どころではなくなってしまった。困った。イエスに香油を注ぎに来た女が福音書記者とハグしてたよ...どうしたらいいんだ...)
アムステルダム・バロック管弦楽団, トン・コープマン指揮。2005年、2日に分けてやった模様。英語字幕付き。
ライプツィヒ・ゲヴァントハウス管弦楽団、指揮はゲオルク・クリストフ・ビラー、福音書記者はマルティン・ペッツォルトという人、1998年。音質がちょっと悪いかな?
サイトウ・キネン・オーケストラ、小澤征爾指揮, 福音書記者ジョン・マーク・エインズリー、1997年。ありがたいことに日本語字幕付きである。
ブランデンブルク・コンソート, スティーヴン・クレオバリー指揮, 福音書記者はRogers Covey-Crumpという人。1994年。
ミュンヘン・バッハ・コレギウム, エノッホ・ツー・グッテンベルク指揮。福音書記者はクレス=ホーカン・アーンショーという人。2015年投稿だがかなり古い演奏だと思う。→1990年の演奏とのこと。
よくわかんないけど、指揮はニコラウス・アーノンクールらしい。1985年。残念ながら音質も画質もよくない。
ミュンヘン・バッハ管弦楽団、カール・リヒター指揮、1971年。すごい、こんな映像があるんですね。英語字幕つき。調べてみたら、どうやらDVDになっている模様。
というわけで、この危機的事態がいつまで続くのかわからないが、バッハの長い曲など聞きつつ、なすべきことをなし、事態が収束するか自分も感染して死ぬのを待つことにしよう。
2020年3月22日 (日)
Tポイントとかdポイントとか、ああいうロイヤリティ・プログラムの「ポイント」についての資料。仕事の関係で目を通した。論文じゃないけど、読んだものは何でも記録しておこう、ということで...
翁百合(2019) ポイント経済化について -マクロ経済や金融システムへのインプリケーションを探る-. 日本総研リサーチレポート, 2019-010.
概観:
- NRIによれば2018年度のポイント発行額は9546億円。これは企業の売上とかにポイント適用率と還元率をかけて推計している。いっぽう金融庁は引当金(負債に属する)の合計額の推移を調べている。
- クレカ・家電量販・携帯電話で発行額が多い。伸びているのはプラットフォーマー企業のポイント。
- ポイントの利用率(失効率)はよくわからない。
- ポイント交換のネットワークは複雑化している。必ずしも交換が進んでいるわけではない。交換自体をビジネス化する動きもある(ネットマイルとか)。
- プラットフォーマーはキャッシュレス決済の経済圏をつくりポイント付加で囲い込みを図っている。
- ポイントを投資に転換する動きもある。これについては金融庁が前向きな方針を示している [←へー]
ミクロにみると、個社発行ポイント(プラットフォーマーでない企業のポイント)とは、企業が消費者の価格弾力性に注目し、将来の値引き分の決済手段をトークンとして渡すもの。いっぽうプラットフォーマーは、還元額の多くを加盟店に負担させる形でトークンを付与する、というちがいがある。
プラットフォーマーがポイント還元を積極的に活用するとなにがおきるか? 3つにわけてみていく。
A. 消費の質の変化。先行研究ではふたつの視点がある。
A1. ポイントがスイッチングコストとして作用し、ロックインが起きる。この観点からいえばポイント交換はスイッチングコストを下げる。
A2. 行動経済学的視点でいうと、ポイント付与の表現を工夫したり参照点を変えたりしてフレーミング効果を起こす。[このくだりは先行研究列挙に近い。寺地・近(2011行動経済学), 泉谷(2013放送大の紀要), 中川(2015行動経済学), 山本(2011立教の紀要), Liu(2007 J.Mktg)]
というわけで、ポイントはロックインにより消費者余剰を低下させている可能性がある。また、キャッシュレス化、データ活用による個別消費提案、消費者行動の非合理化(ポイントを貯めるための貯めるための追加消費とか)が起こりうる。
B. 価格のカスタム化。先行研究ではポイントを非線形プライシングととらえる見方がある。また、企業は景気が悪くなると囲い込んだ顧客に高めの価格をつける傾向があるので、counter cyclicalな効果があるかもといわれている。
というわけで、物価指数が実態から離れるかも。なお、プラットフォーマー型ポイントは価格決定力が加盟店にないからcounter cyclicalな効果は小さかろう。
C. ポイントの疑似貨幣化。先行研究では...[中略]。ただし、仮に年5000億のポイントが決済に使われているとしても、電子マネーの決済金額は約5.5兆、それほど大きくない。また、1単位当たりの価値がばらばらだし交換が限定されているし期限があるし還流しない。貨幣の3機能(価値尺度、流通手段、価値貯蔵)をすべて満たさない。今後のプラットフォーマー型ポイントの進展によってはわかんないけど。
むしろポイントを貯めること自体に楽しみを見出す人も多いわけで、法定通貨にない魅力があるのかもしれない。貨幣の多様性の展望を拓くものともいえる。
云々。
... いっちゃなんだけど、もう少し体裁に気を配ればいいのに、と思った。ちゃんと校正するとか、数式を数式フォントで書くとか。こういうのを読む専門家の方は、そのへんあんまし気にしないのかなあ...
ポイントについての研究を探すとみつかるのはたいてい購買をアウトカムにとった行動経済学的な話なんだけど(ポイント付与と値引きがどう違うかとか)、そうじゃなくて、ポイント獲得行動そのものといえばいいのか、ケインズのいう貨幣愛ならぬポイント愛といえばいいのか、この資料でいうとCの最後の論点に関心があって、理論面での先行研究を探しているんだけど、見当たらない。このレポートでもアンケートを紹介しているだけだった。ううむ。
論文:マーケティング - 読了:翁(2019) マクロ経済に対する「ポイント」の影響
2020年3月19日 (木)
コロナ騒動で気が休まらない毎日でありますが、感染者数の推移や予測がメディアにさかんに取り上げられていて、ああ、こういう研究ができたら面白かったろうな... などと無責任なことをぼんやり考えていた次第である。
で、フォルダを整理していたら、「いずれ読む」PDFのフォルダにそっち方面の概説論文がはいっているのをみつけた。全然覚えていないんだけど、仕事の参考になるかと思って深く考えずに保存していたのだと思う。
せっかくなので、仕事の待ち時間にめくってみた。
西浦博, 稲葉寿 (2006) 感染症流行の予測:感染症数理モデルにおける定量的課題. 統計数理, 54(2), 461-480.
まずはSIRモデルから。
感染する可能性のある人を$S$, 感染している人を$I$, 免疫を獲得したか死んだ人を$R$として、
$\frac{dS(t)}{dt} = -\beta S(t) I(t)$
$\frac{dI(t)}{dt} = \beta S(t) I(t) - \gamma I(t)$
$\frac{dR(t)}{dt} = \gamma I(t)$
$\beta$は感染率。$\beta I(t)$を感染力という。$\gamma$は回復率や隔離率で、$\gamma^{-1}$を感染期間が指数分布に従うと仮定した平均値とする。短期的な流行のモデルなので人口動態は無視する。
総人口を1として、平衡状態$(S(t), I(t), R(t)) = (1,0,0)$において
$\frac{dI(t)}{dt} = (\beta - \gamma) I(t)$
が成り立つ。感染初期に感染者は$I(t) \approx I(0) \exp{(\beta -\gamma)t}$と指数関数的に増えるわけだ。病気が集団に侵入可能になるのは$\beta - \gamma > 0$のときである。ここから
$R_0 = \frac{\beta}{\gamma}$
を基本再生産数という。R noughtと発音する。[←完璧な門外漢なので、このくだりを読んだだけでもう元をとったという感じだ。SIRモデルについては読んだことがあったけど、いまメディアでみかける基本再生産数って全然意味がわかってなかった]
時刻 $t$までに感染を経験した人を $N(t) = S(0) - S(t)$とすると... [残念ながらこの段落は知識不足で理解できなかったので、メモも省略。シグマ代数ってなに?]
SIRモデルの拡張。
$I$をさらに、曝露したけどまだ感染性を持たない状態$E$と感染性を持つ状態$I$にわけると
$\frac{dS(t)}{dt} = -\beta S(t) I(t)$
$\frac{dE(t)}{dt} = \beta S(t) I(t) - \epsilon E(t)$
$\frac{dI(t)}{dt} = \epsilon E(t) - \gamma I(t)$
$\frac{dR(t)}{dt} = \gamma I(t)$
$\epsilon$は「曝露後に感染性を得る率」。これをSEIRモデルという。
ほかにもモデルが作れる。免疫が獲得できないSIRSモデルとか。
基本再生産数の意義として、予防接種率の達成目標について考えると...
効果$\epsilon$のワクチンを接種率$p$で実施したとき、免疫を持たない人の割合は$1-\epsilon p $だから、接触パターンがhomogeneousなら再生産数は$(1-\epsilon p) R_0$。これを1未満にすれば感染症は終息する。$p$について解くと $p > 1 / \epsilon (1-1/R_0)$だ。[←うぉー おもしれええ]
$R_0$の推定は、さすがに決定論的に考えてると精度とかを考慮できないので、確率論的なモデルを考えて...[めんどくさいからメモは省略するけど、そんなにものすごく難しい話ではなさそう。ふつうはML推定量が閉形式で書き下ろせるらしい。$\beta$の時間変動とか感受性の異質性とかを考慮したモデルをMCMC推定したりするのもあるのだそうだ。ふへえええええ]
実際には伝播能力は行動の変化とか公衆衛生施策とかで時間変動するので、そういうのを考慮したのを効果的再生産数($R_t$)という。実際の感染ネットワークから求めたり、理論的に求めたりできる。SARSの流行時にWHOが緊急事態のアラートを出した直後に$R_t$が1未満になったという研究があるそうだ[←へえええええ!]
感染待ち時間・感染性期間の分布を天下りに与えるのではなく、観察に基づき適切な分布を推定するというアプローチもある。
感染待ち時間は潜伏期間と似ているので(潜伏期間の途中から感染性があることが多いから、ほんとはちょっとちがうんだけど)、調査で調べた潜伏期間の分布で代用したりする(対数正規分布に従うことが多い)。検疫に必要な目安の時間がわかったりする。[途中から難しくなってきたので大幅中略]
いっぽう感染性期間の分布を知るのは難しい。感染待ち期間と潜伏期間は似ていることが多いけど、感染性期間と症候性期間はちがう。たとえばHIVの場合、感染した直後にウィルスが多く、いったん下がってAIDS発症の前にまた上がる。[...] 実際のウィルス量と疫学的な感染性との評価指標との相関はまだ確実でなく、今後の課題である。[←へえー。個人レベルの機序と集団レベルの現象の関係が意外にはっきりしないってことなのね... ウィルス量の増減も人によっていろいろってことかしらん]
接触性の異質性を考慮するという方向の拡張もある。[...中略するけど、ひとつのアプローチはそのなかでは接触パターンが均一であるような複数のsubpopulationを考えるという方法で、これをmultitype epidemicモデルというのだそうだ。よくわかんないけど潜在クラスモデルみたいになるのだろうか...]
最近関心が集まっているのは、接触関数の頻度分布がべき乗分布に従うとき(スケールフリーなとき)で、感染症の制圧は困難を極める。
接触頻度に関する定量的説明は性感染症から明らかになるだろうと期待されている。接触回数の計数が観察可能だから。[←これ、誰と何回セックスしたかインタビューで正直に答えるだろうから、って意味だろうか...?]
あれこれ考えているとどんどん複雑になるので、観察データじゃなくて介入研究でパラメータ推定することも多い。[←うぉー面白い!と思ったんだけど、どういう実験になるのか想像がつかなかった...]
云々、云々。
...半分くらいはちんぷんかんぷんだったんだけど、仕事と直接関係しないという気楽さもあって、いやー、面白かった。もっと頭がよくて若かったら、こういうのやりたかったなあ... (← 一時の気の迷い)
ともあれ、研究者の方々のご奮闘をお祈りいたします。
論文:データ解析(2018-) - 読了:西浦・稲葉(2006) 感染症流行の予測
2020年3月11日 (水)
仕事の都合であれこれ考えていたらわけがわからなくなってしまったので、ちょっとシミュレーションをやってみたら、さらに新たな疑問が生じ... という話を記録しておく。
背景
ある量的変数の時系列 $Y_t$ があって、それに影響を及ぼしているであろうなんらかの変数の時系列$X_t$があるとする。なんでもいいんだけど、たとえば売上と広告出稿量とか。
で、$Y_t$に対する$X_t$の効果の大きさをデータから推定したい。こういうこと、よくありますよね。
話を簡単にするために、分析者は次のことを知っているとしよう。
- $X_t$の$Y_t$に対する効果は即時的、かつ線形である。つまり、
$Y_t = \alpha + \beta X_t + V_t$
とモデル化できる。 - $X_t$は定常である。なんでそんなことを知っているのかわからんが、なにか実質的な知識があるのでしょう。
- $Y_t$の撹乱項$V_t$は一次自己回帰過程 (AR(1)過程)に従う。つまり、
$V_t = \rho V_{t-1} + E_t, \ \ E_t \sim N(0, \sigma_E^2)$
とモデル化できる。これも、まあ、ありそうな仮定ですわね。時系列の自己相関関数を観察した結果、これAR(1)でいいんじゃね? と思うことはさほど珍しくないと思う。 - 自己回帰係数$\rho$は$0 \leq \rho \leq 1$である。つまり、$V_t$は非負の自己回帰係数を持つ定常AR(1)過程に従う($0 \leq \rho <1$)か、単位根AR(1)過程に従う($\rho = 1$)かのどちらかである。これもそれほど変な仮定ではないと思う。自己回帰はふつう正だし、もし負だったらデータの観察でそれと気がつくだろう。仮に$\rho >1$なら$V_t$はどっかに飛んでいってしまうはずなので、これも除外できる。でも、$\rho <1$か$\rho = 1$かは簡単には判断できない。
問題
さて、分析者が関心を持っているのは$\beta$である。ここで疑問なのは、$\beta$の推定誤差は$\rho$とどういう風に関連しているのか、という点である。特に次の点について知りたい。
- Q1. $\rho$が大きいとき、つまり結果変数の撹乱項が高い自己相関を持つとき、$\beta$の推定誤差は大きくなるか、それとも小さくなるか。
- Q2. $\rho = 1$であるのにそれと知らず、$\rho < 1$と仮定するモデルを推定したとき、$\beta$の推定誤差は大きくなるか。
いずれも、私にとってはちょっと切実な疑問だ。
Q1についていえば... 仕事のなかで時系列データの分析が生じる際、まずは目的変数の時系列を観察して、これからわざわざ説明変数のデータを集めモデリングする労力は報われるかしらん? と算段することが多いと思う。そういう場面での手掛かりがほしい。見通しが暗いなら早めに白旗を上げたい。
Q2についていえば... 理屈の上からいえば、$\rho=1$かそうでないかでAR(1)過程の挙動はがらっとかわる。でも、実データの背後にあるデータ生成プロセスが$\rho=1$かどうかなんて、どうせわかりっこない。だから、きっと$\rho<1$だよねと信じてAR(1)誤差を仮定したり、いや$\rho=1$にちがいないと信じて差分時系列を分析したりするわけである(そんなことないですか?)。でも心には常に不安の影が付きまとう。$\rho$についての仮定をしくじることが、$\beta$の推定にとってどのくらい致命的なのかを知りたい。
方法
気になって夜も眠れないので(大げさな表現)、簡単なシミュレーションをやってみました。
$t=-100,\ldots,100$について、データを次のように生成した。
$x'_t \sim unif(0, 1)$
$e_t \sim N(0, 1)$
$v_t = \rho v_{t-1} + e_t$
$y'_t = x't + v_t$
つまり$\beta = 1$である。で、$x'_t, y'_t$から$t=1$以降を切り出し、それぞれを中心化する。これを$x_t, y_t$とする。
$\rho$を$0, 0.1, 0.2, \ldots, 1.0$の11通りに動かし、それぞれについて1000個のデータセットを生成した。
それぞれについてデータセットをひとつ選び$x_t, y_t$を描画すると、こんな感じである。
モデルの推定方法として、次の6つを試す。
- A. 単にOLS推定
- B. Rのforecast::Arima()でML推定
- C. Rのnlme::gls()でFGLS推定
- D. 状態空間モデルとして定式化し、RのKFASパッケージを使ってカルマンフィルタで推定
- E. Mplusでベイズ推定
- F. Stanでベイズ推定
推定にあたっては、次の5つのアプローチを試してみる。
- アプローチ1. $\rho = 0$と仮定して、
$y_t = \beta x_t + e_t$
$e_t \sim N(0, \sigma_e^2)$ - アプローチ2. $|\rho| < 1$と仮定して、
$y_t = \beta x_t + v_t$
$v_t = \rho v_{t-1} + e_t, \ \ |\rho| < 1$
$e_t \sim N(0, \sigma_e^2)$ - アプローチ3. $\rho = 1$と仮定し、$\Delta y_t = y_t - y_{t-1}, \Delta x_t = x_t - x_{t-1}$について、
$\Delta y_t = \beta \Delta x_t + e_t$
$e_t \sim N(0, \sigma_e^2)$ - アプローチ4. $y_t$について単位根検定を行い、単位根を持たないと判断されたらアプローチ2, 持つと判断されたらアプローチ3に進む。
- アプローチ5: アプローチ2と同じなんだけど、$\rho$の範囲について仮定しない。
私の乏しい理解では、A(OLS), B(ML), C(FGLS)では撹乱項の定常性が仮定されるので、アプローチ5は選べない。いっぽうD(カルマンフィルタ), E,F(ベイズ)では、$\rho$を明示的に制約しないかぎりアプローチ5になる... というように理解しているのだけれど、ここ、全然自信がない。悲しい。誰か私に教えてくださらないでしょうか。
まあいいや!とにかくシミュレーションしてみたのであります。
単位根検定
まず、アプローチ4で必要になる単位根検定の結果について紹介しておく。Dickey-Fuller検定を使った。Rコードはこんな感じ。$y_t$がdfIn$y_centeredにはいっている。
library(urca)
oDFTest <- ur.df(dfIn$y_centered, type = "none", lags = 1)
nD <- if_else(oDFTest@teststat[1,1] < oDFTest@cval[2], 0, 1)
トレンドもドリフトもないAR(1)であると知っているので、type ="none", lags=1と決め打ちしている。$H_0: \rho=1$が 5%水準で棄却されたら$\rho<1$と判断し、そうでなかったら$\rho=1$と判断することにして、後者の場合にnDを1としている。
素朴に考えると、本当は$\rho=1$であるデータセットのうち95%くらいが$\rho=1$と判断されてほしい($H_0$が真のときに誤って棄却される確率は5%であってほしい)。本当は$\rho<1$である場合は、なるべく多くのデータセットが$\rho<1$と判断されてほしい。
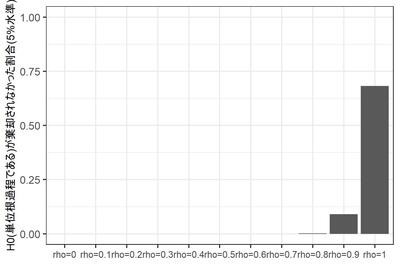
さて、11通りの$\rho$の、それぞれ1000個のデータセットのうち、$\rho = 1$と判断されたデータセットの数は?
蓋をあけてみると... $\rho=1$であるデータセットのうち、$H_0$が棄却されなかった($|\rho|=1$と判断された)データセットは95%には到底及ばず、実に68%にとどまる。なぜだろう? よくわからない。
$\rho<1$であるにもかかわらず$H_0$が棄却されないデータセットは、当然ながら$\rho$が1に近づくにつれて増えるのだが、それでも$\rho = 0.9$のときに9%。$\rho = 0.8$までではほとんど生じない。
このように、DF検定の場合、保守側($H_0: \rho = 1$が棄却されない側)に大きくバイアスがかかるようだ。$H_0$を反対側に設定するPP検定であればまた違う結果になるだろうけど...
まあとにかく、ここで確認しておきたいのは、$\rho = 1$かそうでないかなんて、そんなに簡単にはわからないよね、ということである。
選手紹介
お待たせしました、選手入場です。拍手でお迎え下さい。
A. 単にOLS推定。アプローチ1($\rho=0$と仮定)のRコードは
oModel <- lm(y_centered ~ 0 + x_centered, data = dfIn)
自己相関を華麗にスルーしちゃうわけだが、これ、それほど捨てたもんじゃないと思う次第である。だって、$|\rho| < 1$であれば、$\hat{\beta}$は少なくとも一致推定量ではあるわけでしょう?
アプローチ1, 3($\rho=1$と仮定)を試してみる。
B. forecast::Arima()で最尤推定。Rによる時系列モデリングの定番 forecast パッケージはArima()という関数をご用意している(実はstat::arima()へのラッパーである)。アプローチ2($|\rho|<1$と仮定)のRコードはこんな感じ。
library(forecast)
oModel <- Arima(
y = dfIn$y_centered,
include.mean = FALSE,
order = c(1, 0, 0),
xreg = dfIn$x_centered ,
method = "ML"
)
アプローチ3($\rho=1$と仮定)ならorder = c(0,1,0)となる。アプローチ2, 3, 4(DF検定で切り替え)を試す。
C. nlme::gls()でFGLS推定 ついでにnlme::gls()でFGLS推定を試してみる。計量経済学の教科書に載っているのは、最尤推定じゃなくてこっちのほうですね。
アプローチ2($|\rho|<1$と仮定)のRコードはこんな感じ。
library(nlme)
oModel <- gls(
y_centered ~ 0 + x_centered,
corr = corARMA(p=1, q=0),
data = dfIn
)
アプローチ2のみ試す。
D. 状態空間モデルとして定式化し、RのKFASパッケージを使ってカルマンフィルタで推定。おさらいすると、アプローチ2,5のモデルは
$y_t = \beta x_t + v_t$
$v_t = \rho v_{t-1} + e_t, \ \ e_t \sim N(0, \sigma_e^2)$
である。これを状態空間表現に書き換えよう。状態変数は$\beta$と$v_t$だと考え、縦に積んで$\alpha_t = [\beta, \ v_t]'$としよう。
観察方程式は
$Y_t = Z \alpha_t$
ただし $Z = [x_t, 1]$である。撹乱項がないことに注意。状態方程式は
$\alpha_t = T \alpha_{t-1} + R \eta, \ \ \eta \sim MVN(0, Q)$
遷移行列$T$は2x2の対角行列で、対角要素は$1, \rho$である。$R$は2x2の単位行列で、状態撹乱項は$\eta = [0, e_t]'$とする。共分散行列$Q$は2x2で、右下に$\sigma_e^2$がはいり、残りが0。
こいつをカルマンフィルタで推定する。Rコードはこんな感じ。遷移行列$T$に未知パラメータが入っているので、ちょっと面倒くさい。
library(KFAS)
mgZ <- array(dim = c(1, 2, nrow(dfIn)))
mgZ[1,1,] <- as.vector(dfIn$x_centered)
mgZ[1,2,] <- 1
oModel <- SSModel(
dfIn$y_centered ~ -1 + SSMcustom(
Z = mgZ,
T = matrix(c(1, 0, 0, 1), nrow = 2), # 最後の要素がrho
R = matrix(c(1, 0, 0, 1), nrow = 2),
Q = matrix(c(0, 0, 0, 1), nrow = 2), # 最後の要素がsigma_e
P1 = matrix(c(0,0,0,0), nrow = 2),
P1inf = matrix(c(1,0,0,1), nrow = 2)
),
H = matrix(0)
)
sub_update <- function(par, model){
# par: (sigma_eの対数, rho)
# model: 現在のモデル
model$T[2,2,1] <- par[2]
model$Q[2,2,1] <- exp(par[1])
return(model)
}
oFitted <- fitSSM(
oModel,
inits = c(log(var(dfIn$x_centered)/2), 0.5) ,
updatefn = sub_update,
lower = c(-10, -2),
upper = c(+10, +2),
method = "L-BFGS-B"
)
oEstimated <- KFS(oFitted$model)
計算の都合上$|\rho| < 2$と制約しているものの、このモデルは$|\rho| = 1$という仮定を置かないモデル、つまりアプローチ5ということになると思うのですが... 正しいでしょうか?
E. Mplusでベイズ推定。ここまではRなどという古くさい言語を使っておりましたが、いけてる分析者なら、ここは当然 Mplus ですよね! (すいません冗談です)
構造方程式モデリングの世界ではもはや標準となっているソフトウェア Mplus だが、実はN=1の時系列分析についても便利な機能を持っているのである。
Mplusのコードはこんな感じ。
DATA:
FILE = est2.dat;
VARIABLE:
NAMES = y x;
MISSING=.;
ANALYSIS:
ESTIMATOR = BAYES;
BITERATIONS = (2000);
MODEL:
v by (&1);
v;
v on v&1;
y on v@1 x;
[y@0];
y@0;
MODELコマンドがわかりにくいが、1行目は「vは潜在変数ですが指標を持っていません。モデルのなかでラグ1を使わせて下さい」。2行目は「その残差分散(つまり$\sigma_e$)を自由推定したいです」。3行目で$v_t$の自己回帰を定義し(v&1とは$v_{t-1}$を表す)、4行目で$y_t$のモデルを定義している($v_t$の回帰係数は1に固定している)。ほっとくと$y_t$の切片と残差分散を推定してしまうので、最後の2行でそれを抑止している。
このとき$v_t$の自己回帰係数($\rho$)は範囲が制約されていない、つまりアプローチ5だ、というのが私の理解なのだが、正しいだろうか...?
F. Stanでベイズ推定。ほんとはここまでやるつもりはなかったんだけど、毒も食らわば皿まで、ということで... Stanファイルはこんな感じ。
data {
int T;
vector[T] y;
vector[T] x;
}
parameters {
real beta;
real<lower=-1, upper =1> rho;
real<lower=0> sigma;
}
model {
vector[T] v;
v = y - beta * x;
v[1] ~ normal(0, sigma/sqrt(1-rho^2));
v[2:T] ~ normal(rho * v[1:(T-1)], sigma);
} 下から3行目、v[1]でなにか変なことを書いているが、これは$v_{t-1}$が未知であるときの$v_t$の周辺分布の分散が、$v_{t-1}$の下での$v_t$の条件つき分布の分散 $\sigma_e$より大きくなるからである。
どのくらい大きくなるかというと、
$v_t = \rho v_{t-1} + e_t$
の両辺の分散をとって
$Var(v_t) = Var(\rho v_{t-1} + e_t)$
$e_t$と$v_{t-1}$との共分散は0なので、
$Var(v_t) = \rho^2 Var(v_t) + \sigma_e^2$
ここから
$Var(v_t) = \sigma_e^2 / (1-\rho^2)$
である。
というわけで、尤度計算に当たってデータ点ひとつも無駄にしまいという質実剛健な精神に則り、v[1]についても誠意を込めて分布を書いてみたんだけど、でもこれって、$1-\rho^2 \neq 0$、つまり$|\rho| \neq 1$という仮定を暗黙のうちに含んでいないだろうか? そんならいっそ、というわけで、parametersブロックではreal <lower=-1, upper =1> rho; と書いた次第である。
このモデルとともに、parametersブロックでrhoの範囲制約をなくし、かつ下から3行目を消したモデルも推定してみた。前者はアプローチ2, 後者はアプローチ5に相当すると思うんだけど... うーーん、こういう理解で正しいのだろうか? からきし自信がない。
まとめると、出場選手は以下の10名である。
- A1: OLS推定, $\rho = 0$と仮定
- A3: OLS推定, $\rho = 1$と仮定
- B2: 最尤推定, $|\rho| < 1$と仮定
- B3: 最尤推定, $\rho = 1$と仮定
- B4: 最尤推定, 単位根検定に基づきモデル選択
- C2: FGLS推定, $|\rho| < 1$と仮定
- D5: カルマンフィルタ
- E5: ベイズ推定(Mplus)
- F2: ベイズ推定(Stan), $|\rho| < 1$と仮定
- F5: ベイズ推定(Stan)
推定の様子
この10人の選手に、11水準の$\rho$の各1000個のデータセットについて、$\beta$を推定させた。ただしStanは時間がかかるので、1000個のうち100個だけについて推定するだけで勘弁してやった。
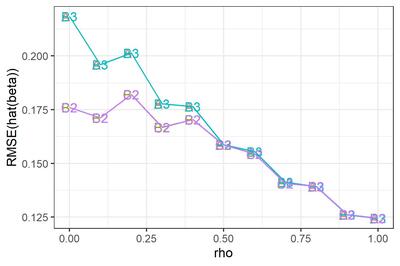
いったいなにをやっているのか、自分でもよくわかんなくなってきたので、選手B2(最尤推定, $|\rho| < 1$と仮定)による推定結果を図にしてみた。
点はデータセット、横軸は$\beta$の推定値, 縦軸は$\rho$の推定値である。真値が赤で表現してある。こうしてみると、真の$\rho$が1に近づくにつれ、$\rho$の推定値は0に向かって歪むみたいですね。横軸と縦軸の間にはあまり相関がなさそうだ。
さて、関心があるのは、$\beta$の真値すなわち 1 と、$\beta$の推定値$\hat{\beta}$とのずれである。その大きさを次の2つの指標で評価しよう。
- バイアス。$\hat{\beta}$の平均から1を引いた値。0に近くないと困る。
- RMSE、すなわち$(\hat{\beta}-1)^2$の平均の平方根。0に近いほうがありがたい。
結果
大変ながらくお待たせいたしました!お待たせしすぎたかもしれません! (ちょっと懐かしい冗談だ)
結果発表です!
選手F2, F5のみ試行回数が100である点に注意。
シンプルなチャートだが、なかなか情報量が多いので、順にみていこう。
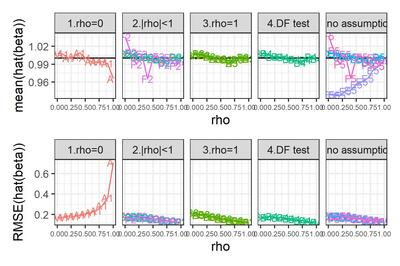
まずは、$\rho = 0$と勝手に想定し、OLS回帰をやってしまった場合。
真の$\rho$がそれほど大きくなければバイアスはそれほど大きくない。しかしRMSEは$\rho$とともに増大する。$\rho$が1に近づくと、バイアス・RMSEともに急増する。なるほど、撹乱項が非定常に近づいているわけだから、パラメータがうまく推定できないのも道理である。
やっぱりあれですね、時系列を分析する際には、きちんと自己相関を考慮することが大事ですね。
次に、$|\rho|<1$と決め打ちした場合(図のパネル2)と、$\rho=1$と決め打ちした場合(パネル3)について。バイアスはそれほど大きくないようだ。RMSEのみ拡大して示す。なお、選手F2はあとで観察することにして、ここでは省略する。
選手B2とC2, 選手B3とA3はぴったり重なってしまっている。つまり、$|\rho|<1$と決め打ちする場合、最尤推定するかFGLS推定するかにはたいしたちがいがないわけだ。$\rho=1$と決め打ちする場合に差分をとって最尤推定するかOLS推定するかも... そりゃそうか、きっと推定値は同じだ。
$\rho$が小さいとき、$\rho=1$と決め打ちするとRMSEが大きくなる。誤ったモデルを指定したわけだから、これは当然である。
これをみて大変に意外だった点がふたつある。
第1に、$\rho$が大きくなるにつれ、つまり撹乱項の自己相関が大きくなるにつれ、$\beta$のRMSEが小さくなっているという点である。$e_t$の分散が同じなら$\rho$が大きいほど撹乱項$v_t$の分散は大きくなるんだから、直感的には、$\beta$の推定はより難しくなるんじゃないかと思ったんだけど... なぜだろう???
もうひとつ、ふへええと言葉にならないため息をついたのは、$\rho$が1に近づくほど、$|\rho|<1$と仮定して定常AR(1)撹乱項を持つ回帰モデルを推定しても、$\rho=1$と仮定して差分時系列について回帰モデルを推定しても、違いがなくなってしまう点である。さきにみたように、単位根検定がしくじりやすいのは$\rho$が1に近いときである。そういうときほど、実は間違えたところでたいした実害はないわけだ。
このように、単位根検定でモデルを切り替えようが、頭から$|\rho|<1$と信じこんで定常AR(1)撹乱項を持つ回帰モデルを使い続けようが、ほとんどちがいがないようだ。たとえ$\rho=1$だったとしても、である。
ええええ? わざわざ単位根検定をやったのに、意味なかったわけ...?
最後に、$\rho$の範囲について制約しないモデル。
元の図にもどると、選手E5がとんでもないバイアスを持っていることがわかる。どうしたんだMplus! しっかりしろ! 医者だ、医者を呼べ!!
... 冗談はともかく、ひょっとすると私がコードを間違えているのかもしれない。残念ながらMplusくんは休場とし、他の選手についてRMSEを拡大してみよう。
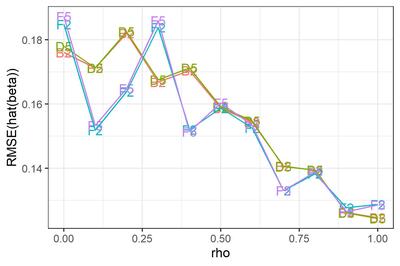
選手D5 (カルマンフィルタ) について。参考のために選手B2 (最尤推定) と並べてみた。ほとんど変わらない。
恥かしながらわたくし、撹乱項の定常性を仮定しているB2は$\rho=1$に近づくとだめになるが、定常性を仮定していないD5はうまくいく... という結果になるかな、と思っておりました。不明を恥じる次第であります。へええ、そうなのかー。
選手F5(Stanでベイズ推定)について。D5との優劣ははっきりしない。参考のためにF2 ($|\rho|<1$と仮定してStanでベイズ推定)と並べてみたところ、$\rho$が小さいところではF2が僅差で勝つが(そりゃそうだ、F2は正しい制約を追加しているわけだから)、$\rho$が1に近づくと僅差で負けるようだ。
まとめ
というわけで、シミュレーションの結果わかったことをまとめておくと、
- Q1. 時系列回帰モデル$Y_t = \alpha + \beta X_t + V_t$において、撹乱項$V_t$が高い自己相関を持つとき、$\beta$の推定誤差は大きくなるか、それとも小さくなるか。→小さくなる。
- Q2. $V_t$の自己回帰係数が1であるのにそれと知らず、1未満と仮定するモデルを推定したとき、$\beta$の推定誤差は大きくなるか。→ならない。
ううむ。どちらも意外な結果であった。勉強が足りないようだ。
それにしても、単位根検定の意味ってなんだろう? 時系列分析の教科書には必ず書いてあるけど、やっても意味なくない? ... と思ってしまったのだが、これは私が「時系列回帰で回帰係数を推定する」という場面だけに焦点を絞っているからで、たとえば予測に関心があるなら話はちがうのかもしれない。
それに、ここでは説明変数時系列が定常であると知っている場合について考えているが、もしそうでなかったら、そりゃあまあ単位根があるかどうか知りたいですわね、みせかけの回帰が怖いから。そういう意味でも、単位根の有無を調べることは、やはり大事なのでありましょう。
なお、この記事のために書いたコードはすべてGithubにアップしております。自己満足もいいところだがな!
2020/03/16追記: 先週書いたこの記事を見直して、はっと気が付いたので記録しておく。
お題は次の通りである。
$y_t = \beta x_t + v_t$
$v_t = \rho v_{t-1} + e_t, \ \ e_t \sim N(0, \sigma_e^2)$
というAR(1)誤差回帰モデルで、$\rho$が大きくなるほど$\hat{\beta}$のRMSEが小さくなるのはなぜか?
2本目の式をラグ演算子$L$を使って書き直すと
$v_t = \rho L v_t + e_t$
$(1-\rho)L v_t = e_t$
ラグ多項式$(1-\rho)L$を$R(L)$とし、
$R(L) v_t = e_t$
と書くことにする。$|\rho| < 1$なら$R^{-1}(L)$が定義できて
$v_t = R^{-1}(L) e_t$
1本目の式に代入して
$y_t = \beta x_t + R^{-1}(L) e_t$
両辺に$R(L)$をかけて
$R(L) y_t = \beta R(L) x_t + e_t$
これは($\rho$を既知とすれば)通常のOLS回帰と同じなので、$x_t^* = R(L) x_t$と略記して
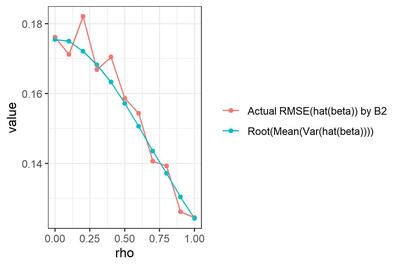
$\displaystyle Var(\hat{\beta}) = \frac{\sigma^2_e}{\sum(x_t^* - \bar{x}^*)^2} $
である。つまり、AR(1)誤差回帰モデルの回帰係数の標準誤差は、ふつうの単回帰のように「撹乱項の分散と独立変数の偏差平方和の比」なのでなく、「AR(1)誤差の裏にあるホワイトノイズの分散と、$x_t - \rho x_{t-1}$の偏差平方和の比」なのである。だから、自己回帰係数が大きいほど分母は大きくなり、$\hat{\beta}$のSEは小さくなるわけだ。うっわー。
オレンジ色は、選手B2による$\hat{\beta}$の、真値($\beta=1$)に対するRMSE (再掲)。青色は、各試行について真の$\rho$を既知として$Var(\hat{\beta})$を求め、試行を通じて平均して平方根をとった値。
な・る・ほ・ど...
雑記:データ解析 - 時系列回帰の撹乱項が自己回帰していると、いったいなにがどうなるのか(追記あり)
2020年2月29日 (土)
Rをつかっているとformulaを書かないといけないことがあるけど(回帰系の関数を呼ぶときとかに)、なんか便利な書き方がありそうなのに全然使っていない。このたび、ふとstats::formula()のドキュメントを眺めていたら、恥ずかしながら「へぇー」と思うことがいくつかあった。
この話題、Rを使っている人にとってはたぶん馴染み深い話で、webをちょっと検索するだけで、丁寧に解説しておられるブログ記事をいくつもみつけることができる(たとえばこちら:[R] 予測モデルを作るには formula を活用せよ)。そういうのをきちんと読んできちんと理解しておけばいいんですけどね。そのときは「へぇー」と思うんだけど、すぐに忘れちゃうのである。
というわけで、今日は忘れないようにメモしておこう。なぜか執事風の丁寧語で。お嬢様、羊肉のソテーでございます、って感じで。
- 「
y ~ model」: 反応yをmodelで指定した予測子でモデル化いたします。 - 「
a + b」:aとbの線形和でございます。 - 「
a : b」:aとbの交互作用でございます。 - 「
a * b」:aとbのクロス、すなわちa+b+a:bでございます。 - 「
(a + b + c)^2」:(a + b + c)の二次のクロス、すなわちa,b,cの主効果と二次交互作用でございます [これ知らなかった... 文字通り展開するとa*a, b*b, c*cが生まれるけど、それらは算術的な意味での$a^2, b^2, c^2$ではなくて、単にa, b, cの主効果ってことになるのね。へー] - 「
a + b %in% a」:bはaにネストしております。すなわちa + a:bでございます。[ここちょっと不思議なところで...%in%は常に:と等価なのかしらん?] 「(a + b + c)^2 - a:b」:(a + b + c)^2からa:bを取り除いたもの、すなわちa + b + c + b:c + a:cでございます。- 「
y ~ x - 1」: 切片項を取り除いております。y ~ x + 0,y ~ 0 + xでもよろしゅうございます [←Rを使い始めたときから、formulaの右辺で0と1が等価だってのが気持ち悪くてしかたない。責任者でてこい] 「log(y) ~ a + log(x)」: このように、算術表現もお使いになれます [←私、formulaのなかでこういう変数変換を掛けるのが生理的に許せなくて、必ず自力で前処理している。なぜ気持ち悪いのかいま気が付いた。formulaのなかの演算子は算術演算子ではないのに(たとえば+は和ではないのに)、関数は算術表現として扱われるというのが気持ち悪いんだ...]- 「
a + I(b+c)」: aとb+cの線形和でございます。I()のなかの演算子は算術演算子として扱われるのでございます。 - 「
.」: 「そのformulaのなかにないすべての列」を表します [←formulaをupdateするときはちがう意味になるのだが、まあupdateなんて使わないからいいや] - 「
a + b + offset(z)」: aとbの線形和とzとの和でございます。zの係数は1となります。なお、この表現は受け付けない関数もございます。
ところで、lm(y ~ a/b)なんていう書き方をみたことがあるけど(y ~ a + a:bと等価だと思う)、stats::formula()のドキュメントにも、stats::lm()のドキュメントにも載ってなかった。あれえ?
雑記:データ解析 - 覚え書き:Rのformulaのなかで使える表現
仕事の都合でときどき混合効果モデルを組みたくなることがある。本腰を入れる場合はMplusを使うけど、ほんのちょっとした用事の場合など、ちょっぴり億劫に感じることもある。RStudioのなかでちゃちゃっと済ませちゃいたいな、なあんて... ううむ、Mplus信者としては敬虔さが足りない、すみませんすみません。
Rでなにかのモデルを組むとき、「どのパッケージを使えばいいんだ...」と困ることがあるけど、混合効果モデルはその典型例だと思う。古株としてはnlme (たしか標準パッケージだ)、lme4があり、さらにはglmmMLだの、glmmだの(あ、2018年で開発が止まったようだ)、かの複雑怪奇なMCMCglmmとか... 参っちゃいますね。
Bates, D., Machler, M., Bolker, B.M., Walker, S.C. Fitting Linear Mixed-Effects Models Using lme4.
というわけで、緊急事態に対応するため、どれでもいいからちょっと土地勘をつけておきたいと思い、lme4パッケージのビニエットに目を通した。発行年が書いてないんだけど、これの古い版は2015年にJ. Statistical Softwareに載っている模様。
ほんとはnlmeパッケージについて調べたかったのだけど、適切な文献が見当たらなかったのである。開発者による解説書、ピネイロ&ベイツ「S-PLUSによる混合効果モデル解析」を読めってことでしょうか。うーん、それは勘弁してほしい。あれは滅茶苦茶むずかしい。
ところが、今回はじめて知ったんだけど、lme4パッケージの筆頭開発者はDouglas Batesさん。ピネイロ&ベイツ本の第二著者、かつてピネイロさんとともにnlmeパッケージを開発した人であった。どうやら、Batesさんは2007年にnlme開発チームを離れ、ライバルとなる新パッケージlme4を作り始めた、ということらしい。へええ。
いわく。
lme4はnlmeと比べ...[さまざまな美点が挙げてある]。いっぽうnlmeは、残差に自己相関のような構造があるモデルとか、ランダム効果の共分散行列に構造があるモデルとかを組むときのUIが優れている。
まずは線形混合モデルから。
線形モデルは、ベクトル値ランダム反応変数$\mathcal{Y}$の分布
$\mathcal{Y} \sim N(\mathbf{X} \beta + \mathbf{o}, \sigma^2 \mathbf{W}^{-1})$
として記述できる。$\mathbf{W}$は対角行列で既知のウェイト、$\mathbf{o}$は既知のオフセット項。パラメータは$\beta$と$\sigma^2$である。
同様に、線形混合モデルは$\mathcal{Y}$とランダム効果ベクトル$\mathcal{B}$の分布として記述できる。$\mathcal{B}=\mathbf{b}$の下での条件つき分布は
$(\mathcal{Y} | \mathcal{B} = \mathbf{b}) = N(\mathbf{X} \beta + \mathbf{Zb} + \mathbf{o}, \sigma^2 \mathbf{W}^{-1})$
$\mathcal{B}$の分布は
$\mathcal{B} \sim N(\mathbf{0}, \mathbf{\Sigma})$
ただし$\mathbf{\Sigma}$は半正定値[すべての固有値が非負ってことね]。これは、分散成分パラメータ$\theta$に依存する相対共分散ファクター$\Lambda_\theta$を考えて
$\Sigma_\theta = \sigma^2 \Lambda_\theta \Lambda_\theta^\top$
と書くと便利である。[こういわれると抽象的で困っちゃいますが... ]
さて、lme4パッケージがご提供する線形混合モデルの関数は lmer() であります。
たとえば...[対象者の睡眠を9日間制限し、毎日反応時間課題をやったというデータの紹介...]。この場合、
lmer(Reaction ~ Days + (Days | Subject), data = sleepstudy)
と書く。
実は、lmer() は以下の4つのモジュールの組み合わせである。
その1, Formula.
parsedFormula <- lFormula(formula = Reaction ~ Days + (Days | Subject), data = sleepstudy)
その2, 目的関数.
devianceFunction <- do.call(mkLmerDevfun, parsedFormula)
その3, 最適化.
optimizerOutput <- optimizeLmer(devianceFunction)
その4, 出力. (めんどくさいのでコードは省略するが、mkMerMod()という関数)
モジュール1, Formulaについて。
formula引数は
resp ~ FEexpr + (REexpr1 | factor1) + (REexpr2 | factor2) + ...
という形式をとる。FEexprは固定効果モデル行列$X$を決める表現。問題はその右側、ランダム効果の項である。
個々のREexprは線形モデルのformulaとして評価される。つまりlm()なんかのformulaと同じである。1と書いたら切片である。factorはRの因子型として評価される。縦棒は、効果とグルーピング因子との交互作用を表すと思えばよい。
いくつか例を挙げると、
(1 | g)は「gの個々の水準がランダム切片を持つ」という意味になる。ランダム切片の平均とSDがパラメータになる。1 + (1 | g)と書いてもよい。- ランダム切片の平均が既知の変数oであるならば
0 + offset(o) + (1|g)と書く。先頭の0は-1と書いてもよい。 - g1の下にg2があって、切片がg1の水準間でもg2の水準間でも動くなら
(1|g1) + (1|g1:g2)と書く。これは(1 | g1/g2)とも書ける。[←へー] - g1とg2がネストじゃなくてクロスしているなら
1 + (1|g1) + (1|g2)と書く。IRTなんかがそうだ(被験者と項目がクロスする)。先頭の1は略記できる。 - 切片と傾きの両方が動くなら
1 + x + (1+x|g)と書く。これはx + (x | g)と略記できる[←えっそうなの? 知らなかった]。lme4では同じランダム効果項に出てくる係数はすべて相関することに注意。つまり切片と傾きは相関する。 - 切片と傾きを無相関にしないなら、
1 + x + (1|g) + (0+x|g)と書けばよい。これはx + (x || g)と略記できる[←へー!]。なお、こういう制約は予測子が比率尺度の場合に限るのが望ましい。この制約の下では予測子をシフトするだけで尤度が変わるから。[←ここ、ちょっとピンとこなかった... いずれ必要になったらゆっくり考えよう]
FEexprから$\mathbf{X}$, その右から$\mathbf{Z}$と$\Lambda_\theta$がつくられる。[以下、$\mathbf{Z}$と$\Lambda_\theta$の作り方について詳しい説明があったけど、半分くらいで力尽きた。メモ省略]
モジュール2, 目的関数モジュールは...[罰則付き最小二乗法によるあてはめの説明とかが12頁にわたって説明されている。読んだところで理解できそうにないのでまるごとパス]
モジュール3. 非線形最適化モジュールは... [ここもどうせわからんので読んでないけど、混合モデルに限らない汎用的な最適化関数らしい。ふーん]
モジュール4. 出力モジュールは... [単に出力の話かと思ったら、意外に仕事が多くて驚いた。まあこれは困ったときに読めばいいかな]
... 途中から面倒になってぱらぱらめくっただけなんだけど、まあいいや。
lme4パッケージの全貌についてのユーザ向け紹介を期待していたんだけど、このビニエットはlmer()の仕組みについて詳しーく説明するものであった。しょうがないのでメモしておくけど、lme4の主力関数は次の3つである。ときに、末尾のerってなんの略なんすかね?
- lmer(): 線形混合モデル
- glmer(): 一般化線形混合モデル
- nlmer(): 非線形混合モデル
nlmeパッケージでいうところのcorrelation = corAR1()のように、誤差項に自己相関を持たせる方法が知りたかったんだけどな... おそらく、lme4でもできなかないけど、めんどくさいのであろう。
論文:データ解析(2018-) - 読了:Bates, et al. (2015?) lme4::lmer()でたのしい線形混合モデリング
<< 読了:「中国 人口減少の真実」